Physics for Scientists and Engineers: Foundations and Connections
1st Edition
ISBN: 9781133939146
Author: Katz, Debora M.
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 16, Problem 35PQ
A uniform annular ring of mass m and inner and outer radii a and b, respectively, is pivoted around an axis perpendicular to the plane of the ring at point P (Fig. P16.35). Determine its period of oscillation.
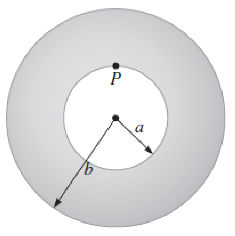
FIGURE P16.35
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
No chatgpt pls will upvote
air is pushed steadily though a forced air pipe at a steady speed of 4.0 m/s. the pipe measures 56 cm by 22 cm. how fast will air move though a narrower portion of the pipe that is also rectangular and measures 32 cm by 22 cm
No chatgpt pls will upvote
Chapter 16 Solutions
Physics for Scientists and Engineers: Foundations and Connections
Ch. 16.1 - Prob. 16.1CECh. 16.2 - Prob. 16.2CECh. 16.2 - For each expression, identify the angular...Ch. 16.5 - Prob. 16.4CECh. 16.6 - Prob. 16.5CECh. 16.6 - Prob. 16.6CECh. 16 - Case Study For each velocity listed, state the...Ch. 16 - Case Study For each acceleration listed, state the...Ch. 16 - Prob. 3PQCh. 16 - Prob. 4PQ
Ch. 16 - Prob. 5PQCh. 16 - Prob. 6PQCh. 16 - The equation of motion of a simple harmonic...Ch. 16 - The expression x = 8.50 cos (2.40 t + /2)...Ch. 16 - A simple harmonic oscillator has amplitude A and...Ch. 16 - Prob. 10PQCh. 16 - A 1.50-kg mass is attached to a spring with spring...Ch. 16 - Prob. 12PQCh. 16 - Prob. 13PQCh. 16 - When the Earth passes a planet such as Mars, the...Ch. 16 - A point on the edge of a childs pinwheel is in...Ch. 16 - Prob. 16PQCh. 16 - Prob. 17PQCh. 16 - A jack-in-the-box undergoes simple harmonic motion...Ch. 16 - C, N A uniform plank of length L and mass M is...Ch. 16 - Prob. 20PQCh. 16 - A block of mass m = 5.94 kg is attached to a...Ch. 16 - A block of mass m rests on a frictionless,...Ch. 16 - It is important for astronauts in space to monitor...Ch. 16 - Prob. 24PQCh. 16 - A spring of mass ms and spring constant k is...Ch. 16 - In an undergraduate physics lab, a simple pendulum...Ch. 16 - A simple pendulum of length L hangs from the...Ch. 16 - We do not need the analogy in Equation 16.30 to...Ch. 16 - Prob. 29PQCh. 16 - Prob. 30PQCh. 16 - Prob. 31PQCh. 16 - Prob. 32PQCh. 16 - Prob. 33PQCh. 16 - Show that angular frequency of a physical pendulum...Ch. 16 - A uniform annular ring of mass m and inner and...Ch. 16 - A child works on a project in art class and uses...Ch. 16 - Prob. 37PQCh. 16 - Prob. 38PQCh. 16 - In the short story The Pit and the Pendulum by...Ch. 16 - Prob. 40PQCh. 16 - A restaurant manager has decorated his retro diner...Ch. 16 - Prob. 42PQCh. 16 - A wooden block (m = 0.600 kg) is connected to a...Ch. 16 - Prob. 44PQCh. 16 - Prob. 45PQCh. 16 - Prob. 46PQCh. 16 - Prob. 47PQCh. 16 - Prob. 48PQCh. 16 - A car of mass 2.00 103 kg is lowered by 1.50 cm...Ch. 16 - Prob. 50PQCh. 16 - Prob. 51PQCh. 16 - Prob. 52PQCh. 16 - Prob. 53PQCh. 16 - Prob. 54PQCh. 16 - Prob. 55PQCh. 16 - Prob. 56PQCh. 16 - Prob. 57PQCh. 16 - An ideal simple harmonic oscillator comprises a...Ch. 16 - Table P16.59 gives the position of a block...Ch. 16 - Use the position data for the block given in Table...Ch. 16 - Consider the position data for the block given in...Ch. 16 - Prob. 62PQCh. 16 - Prob. 63PQCh. 16 - Use the data in Table P16.59 for a block of mass m...Ch. 16 - Consider the data for a block of mass m = 0.250 kg...Ch. 16 - A mass on a spring undergoing simple harmonic...Ch. 16 - A particle initially located at the origin...Ch. 16 - Consider the system shown in Figure P16.68 as...Ch. 16 - Prob. 69PQCh. 16 - Prob. 70PQCh. 16 - Prob. 71PQCh. 16 - Prob. 72PQCh. 16 - Determine the period of oscillation of a simple...Ch. 16 - The total energy of a simple harmonic oscillator...Ch. 16 - A spherical bob of mass m and radius R is...Ch. 16 - Prob. 76PQCh. 16 - A lightweight spring with spring constant k = 225...Ch. 16 - Determine the angular frequency of oscillation of...Ch. 16 - Prob. 79PQCh. 16 - A Two springs, with spring constants k1 and k2,...Ch. 16 - Prob. 81PQCh. 16 - Prob. 82PQ
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- 13.87 ... Interplanetary Navigation. The most efficient way to send a spacecraft from the earth to another planet is by using a Hohmann transfer orbit (Fig. P13.87). If the orbits of the departure and destination planets are circular, the Hohmann transfer orbit is an elliptical orbit whose perihelion and aphelion are tangent to the orbits of the two planets. The rockets are fired briefly at the depar- ture planet to put the spacecraft into the transfer orbit; the spacecraft then coasts until it reaches the destination planet. The rockets are then fired again to put the spacecraft into the same orbit about the sun as the destination planet. (a) For a flight from earth to Mars, in what direction must the rockets be fired at the earth and at Mars: in the direction of motion, or opposite the direction of motion? What about for a flight from Mars to the earth? (b) How long does a one- way trip from the the earth to Mars take, between the firings of the rockets? (c) To reach Mars from the…arrow_forwardNo chatgpt pls will upvotearrow_forwarda cubic foot of argon at 20 degrees celsius is isentropically compressed from 1 atm to 425 KPa. What is the new temperature and density?arrow_forward
- Calculate the variance of the calculated accelerations. The free fall height was 1753 mm. The measured release and catch times were: 222.22 800.00 61.11 641.67 0.00 588.89 11.11 588.89 8.33 588.89 11.11 588.89 5.56 586.11 2.78 583.33 Give in the answer window the calculated repeated experiment variance in m/s2.arrow_forwardNo chatgpt pls will upvotearrow_forwardCan you help me solve the questions pleasearrow_forward
- Can you help me solve these questions please so i can see how to do itarrow_forwardHow can i solve this if n1 (refractive index of gas) and n2 (refractive index of plastic) is not known. And the brewsters angle isn't knownarrow_forward2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward
- 2-3. Consider the situation of the reflection of a pulse at the interface of two string described in the previous problem. In addition to the net disturbances being equal at the junction, the slope of the net disturbances must also be equal at the junction at all times. Given that p1 = 4.0 g/m, H2 = 9.0 g/m and Aj = 0.50 cm find 2. A, (Answer: -0.10 cm) and 3. Ay. (Answer: 0.40 cm)please I need to show all work step by step problems 2 and 3arrow_forwardFrom number 2 and 3 I just want to show all problems step by step please do not short cut look for formulaarrow_forwardPlz don't use chatgpt pls will upvotearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY