Precalculus with Limits: A Graphing Approach
Precalculus with Limits: A Graphing Approach
7th Edition
ISBN: 9781305071711
Author: Ron Larson
Publisher: Brooks/Cole
bartleby

Videos

Question
Book Icon
Chapter 1.4, Problem 5E
To determine

To sketch the graph of the given functions on same co-ordinate system and verify using graphing utility

Expert Solution & Answer
Check Mark

Explanation of Solution

Given:

The given functions are:

  f(x)=xg(x)=x−4h(x)=3x

Calculation for graph:

Consider f(x)=x

    Values of x Values of f (x )
    00
    11
    -1-1
    22
    -2-2

By taking different values of x , the graph can be plotted.

Calculation for graph:

Consider g(x)=x−4

    Values of x Values of g (x)
    0-4
    1-3
    -1-5
    2-2
    -2-6

By taking different values of x , the graph can be plotted.

Calculation for graph:

Consider h(x)=3x

    Values of x Values of h (x )
    00
    13
    -1-3
    26
    -2-6

By taking different values of x , the graph can be plotted.

Graphing above functions on the same co-ordinate system:

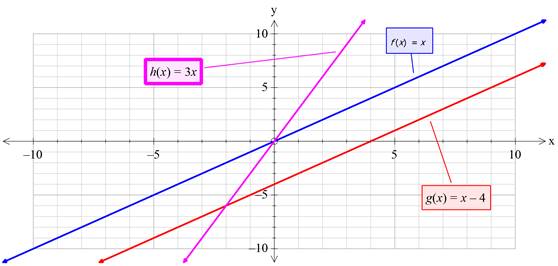
  Precalculus with Limits: A Graphing Approach, Chapter 1.4, Problem 5E , additional homework tip 1

Verification:

Using graphing utility to draw the graph of given functions,

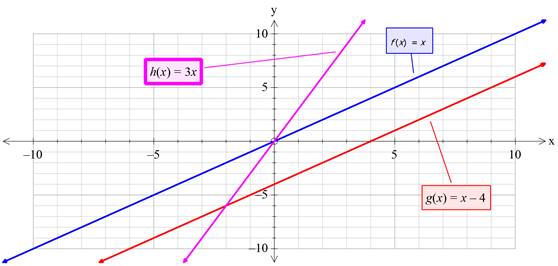
  Precalculus with Limits: A Graphing Approach, Chapter 1.4, Problem 5E , additional homework tip 2

Interpretation:

From above graph, it is clear that, the drawn sketch and above graph are identical to each other.

Here, f(x)=x is the base graph.

  g(x) is the rigid transformation of the base graph with a horizontal shift of 4 units towards right.

  h(x) is the non-rigid transformation of the base graph with a vertical stretch.

Previous
Chapter 1.4, Problem 4E
Next
Chapter 1.4, Problem 6E

Chapter 1 Solutions

Precalculus with Limits: A Graphing Approach

Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10E
Ch. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 17ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.1 - Prob. 64ECh. 1.1 - Prob. 65ECh. 1.1 - Prob. 66ECh. 1.1 - Prob. 67ECh. 1.1 - Prob. 68ECh. 1.1 - Prob. 69ECh. 1.1 - Prob. 70ECh. 1.1 - Prob. 71ECh. 1.1 - Prob. 72ECh. 1.1 - Prob. 73ECh. 1.1 - Prob. 74ECh. 1.1 - Prob. 75ECh. 1.1 - Prob. 76ECh. 1.1 - Prob. 77ECh. 1.1 - Prob. 78ECh. 1.1 - Prob. 79ECh. 1.1 - Prob. 80ECh. 1.1 - Prob. 81ECh. 1.1 - Prob. 82ECh. 1.1 - Prob. 83ECh. 1.1 - Prob. 84ECh. 1.1 - Prob. 85ECh. 1.1 - Prob. 86ECh. 1.1 - Prob. 87ECh. 1.1 - Prob. 88ECh. 1.1 - Prob. 89ECh. 1.1 - Prob. 90ECh. 1.1 - Prob. 91ECh. 1.1 - Prob. 92ECh. 1.1 - Prob. 93ECh. 1.1 - Prob. 94ECh. 1.1 - Prob. 95ECh. 1.1 - Prob. 96ECh. 1.1 - Prob. 97ECh. 1.1 - Prob. 98ECh. 1.1 - Prob. 99ECh. 1.1 - Prob. 100ECh. 1.1 - Prob. 101ECh. 1.1 - Prob. 102ECh. 1.1 - Prob. 103ECh. 1.1 - Prob. 104ECh. 1.1 - Prob. 105ECh. 1.1 - Prob. 106ECh. 1.1 - Prob. 107ECh. 1.1 - Prob. 108ECh. 1.1 - Prob. 109ECh. 1.1 - Prob. 110ECh. 1.1 - Prob. 111ECh. 1.1 - Prob. 112ECh. 1.1 - Prob. 113ECh. 1.1 - Prob. 114ECh. 1.1 - Prob. 115ECh. 1.1 - Prob. 116ECh. 1.1 - Prob. 117ECh. 1.1 - Prob. 118ECh. 1.1 - Prob. 119ECh. 1.1 - Prob. 120ECh. 1.1 - Prob. 121ECh. 1.1 - Prob. 122ECh. 1.1 - Prob. 123ECh. 1.1 - Prob. 124ECh. 1.1 - Prob. 125ECh. 1.1 - Prob. 126ECh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.2 - Prob. 88ECh. 1.2 - Prob. 89ECh. 1.2 - Prob. 90ECh. 1.2 - Prob. 91ECh. 1.2 - Prob. 92ECh. 1.2 - Prob. 93ECh. 1.2 - Prob. 94ECh. 1.2 - Prob. 95ECh. 1.2 - Prob. 96ECh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - Prob. 3ECh. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 66ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.3 - Prob. 70ECh. 1.3 - Prob. 71ECh. 1.3 - Prob. 72ECh. 1.3 - Prob. 73ECh. 1.3 - Prob. 74ECh. 1.3 - Prob. 75ECh. 1.3 - Prob. 76ECh. 1.3 - Prob. 77ECh. 1.3 - Prob. 78ECh. 1.3 - Prob. 79ECh. 1.3 - Prob. 80ECh. 1.3 - Prob. 81ECh. 1.3 - Prob. 82ECh. 1.3 - Prob. 83ECh. 1.3 - Prob. 84ECh. 1.3 - Prob. 85ECh. 1.3 - Prob. 86ECh. 1.3 - Prob. 87ECh. 1.3 - Prob. 88ECh. 1.3 - Prob. 89ECh. 1.3 - Prob. 90ECh. 1.3 - Prob. 91ECh. 1.3 - Prob. 92ECh. 1.3 - Prob. 93ECh. 1.3 - Prob. 94ECh. 1.3 - Prob. 95ECh. 1.3 - Prob. 96ECh. 1.3 - Prob. 97ECh. 1.3 - Prob. 98ECh. 1.3 - Prob. 99ECh. 1.3 - Prob. 100ECh. 1.3 - Prob. 101ECh. 1.3 - Prob. 102ECh. 1.3 - Prob. 103ECh. 1.3 - Prob. 104ECh. 1.3 - Prob. 105ECh. 1.3 - Prob. 106ECh. 1.3 - Prob. 107ECh. 1.3 - Prob. 108ECh. 1.3 - Prob. 109ECh. 1.3 - Prob. 110ECh. 1.3 - Prob. 111ECh. 1.3 - Prob. 112ECh. 1.3 - Prob. 113ECh. 1.3 - Prob. 114ECh. 1.3 - Prob. 115ECh. 1.3 - Prob. 116ECh. 1.3 - Prob. 117ECh. 1.3 - Prob. 118ECh. 1.3 - Prob. 119ECh. 1.3 - Prob. 120ECh. 1.4 - Prob. 1ECh. 1.4 - Prob. 2ECh. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.4 - Prob. 56ECh. 1.4 - Prob. 57ECh. 1.4 - Prob. 58ECh. 1.4 - Prob. 59ECh. 1.4 - Prob. 60ECh. 1.4 - Prob. 61ECh. 1.4 - Prob. 62ECh. 1.4 - Prob. 63ECh. 1.4 - Prob. 64ECh. 1.4 - Prob. 65ECh. 1.4 - Prob. 66ECh. 1.4 - Prob. 67ECh. 1.4 - Prob. 68ECh. 1.4 - Prob. 69ECh. 1.4 - Prob. 70ECh. 1.4 - Prob. 71ECh. 1.4 - Prob. 72ECh. 1.4 - Prob. 73ECh. 1.4 - Prob. 74ECh. 1.4 - Prob. 75ECh. 1.4 - Prob. 76ECh. 1.4 - Prob. 77ECh. 1.4 - Prob. 78ECh. 1.4 - Prob. 79ECh. 1.4 - Prob. 80ECh. 1.4 - Prob. 81ECh. 1.4 - Prob. 82ECh. 1.4 - Prob. 83ECh. 1.4 - Prob. 84ECh. 1.4 - Prob. 85ECh. 1.4 - Prob. 86ECh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.5 - Prob. 52ECh. 1.5 - Prob. 53ECh. 1.5 - Prob. 54ECh. 1.5 - Prob. 55ECh. 1.5 - Prob. 56ECh. 1.5 - Prob. 57ECh. 1.5 - Prob. 58ECh. 1.5 - Prob. 59ECh. 1.5 - Prob. 60ECh. 1.5 - Prob. 61ECh. 1.5 - Prob. 62ECh. 1.5 - Prob. 63ECh. 1.5 - Prob. 64ECh. 1.5 - Prob. 65ECh. 1.5 - Prob. 66ECh. 1.5 - Prob. 67ECh. 1.5 - Prob. 68ECh. 1.5 - Prob. 69ECh. 1.5 - Prob. 70ECh. 1.5 - Prob. 71ECh. 1.5 - Prob. 72ECh. 1.5 - Prob. 73ECh. 1.5 - Prob. 74ECh. 1.5 - Prob. 75ECh. 1.5 - Prob. 76ECh. 1.5 - Prob. 77ECh. 1.5 - Prob. 78ECh. 1.5 - Prob. 79ECh. 1.5 - Prob. 80ECh. 1.5 - Prob. 81ECh. 1.5 - Prob. 82ECh. 1.5 - Prob. 83ECh. 1.5 - Prob. 84ECh. 1.5 - Prob. 85ECh. 1.5 - Prob. 86ECh. 1.5 - Prob. 87ECh. 1.5 - Prob. 88ECh. 1.5 - Prob. 89ECh. 1.5 - Prob. 90ECh. 1.5 - Prob. 91ECh. 1.5 - Prob. 92ECh. 1.5 - Prob. 93ECh. 1.5 - Prob. 94ECh. 1.5 - Prob. 95ECh. 1.5 - Prob. 96ECh. 1.5 - Prob. 97ECh. 1.5 - Prob. 98ECh. 1.5 - Prob. 99ECh. 1.5 - Prob. 100ECh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.6 - Prob. 69ECh. 1.6 - Prob. 70ECh. 1.6 - Prob. 71ECh. 1.6 - Prob. 72ECh. 1.6 - Prob. 73ECh. 1.6 - Prob. 74ECh. 1.6 - Prob. 75ECh. 1.6 - Prob. 76ECh. 1.6 - Prob. 77ECh. 1.6 - Prob. 78ECh. 1.6 - Prob. 79ECh. 1.6 - Prob. 80ECh. 1.6 - Prob. 81ECh. 1.6 - Prob. 82ECh. 1.6 - Prob. 83ECh. 1.6 - Prob. 84ECh. 1.6 - Prob. 85ECh. 1.6 - Prob. 86ECh. 1.6 - Prob. 87ECh. 1.6 - Prob. 88ECh. 1.6 - Prob. 89ECh. 1.6 - Prob. 90ECh. 1.6 - Prob. 91ECh. 1.6 - Prob. 92ECh. 1.6 - Prob. 93ECh. 1.6 - Prob. 94ECh. 1.6 - Prob. 95ECh. 1.6 - Prob. 96ECh. 1.6 - Prob. 97ECh. 1.6 - Prob. 98ECh. 1.6 - Prob. 99ECh. 1.6 - Prob. 100ECh. 1.6 - Prob. 101ECh. 1.6 - Prob. 102ECh. 1.6 - Prob. 103ECh. 1.6 - Prob. 104ECh. 1.6 - Prob. 105ECh. 1.6 - Prob. 106ECh. 1.6 - Prob. 107ECh. 1.6 - Prob. 108ECh. 1.6 - Prob. 109ECh. 1.6 - Prob. 110ECh. 1.6 - Prob. 111ECh. 1.6 - Prob. 112ECh. 1.6 - Prob. 113ECh. 1.6 - Prob. 114ECh. 1.6 - Prob. 115ECh. 1.6 - Prob. 116ECh. 1.6 - Prob. 117ECh. 1.6 - Prob. 118ECh. 1.6 - Prob. 119ECh. 1.6 - Prob. 120ECh. 1.6 - Prob. 121ECh. 1.6 - Prob. 122ECh. 1.6 - Prob. 123ECh. 1.6 - Prob. 124ECh. 1.6 - Prob. 125ECh. 1.6 - Prob. 126ECh. 1.6 - Prob. 127ECh. 1.6 - Prob. 128ECh. 1.6 - Prob. 129ECh. 1.6 - Prob. 130ECh. 1.6 - Prob. 131ECh. 1.6 - Prob. 132ECh. 1.6 - Prob. 133ECh. 1.6 - Prob. 134ECh. 1.6 - Prob. 135ECh. 1.6 - Prob. 136ECh. 1.6 - Prob. 137ECh. 1.6 - Prob. 138ECh. 1.6 - Prob. 139ECh. 1.6 - Prob. 140ECh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - Prob. 9ECh. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - Prob. 15ECh. 1.7 - Prob. 16ECh. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - Prob. 36ECh. 1.7 - Prob. 37ECh. 1.7 - Prob. 38ECh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - Prob. 84RECh. 1 - Prob. 85RECh. 1 - Prob. 86RECh. 1 - Prob. 87RECh. 1 - Prob. 88RECh. 1 - Prob. 89RECh. 1 - Prob. 90RECh. 1 - Prob. 91RECh. 1 - Prob. 92RECh. 1 - Prob. 93RECh. 1 - Prob. 94RECh. 1 - Prob. 95RECh. 1 - Prob. 96RECh. 1 - Prob. 97RECh. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - Prob. 100RECh. 1 - Prob. 101RECh. 1 - Prob. 102RECh. 1 - Prob. 103RECh. 1 - Prob. 104RECh. 1 - Prob. 105RECh. 1 - Prob. 106RECh. 1 - Prob. 107RECh. 1 - Prob. 108RECh. 1 - Prob. 109RECh. 1 - Prob. 110RECh. 1 - Prob. 111RECh. 1 - Prob. 112RECh. 1 - Prob. 113RECh. 1 - Prob. 114RECh. 1 - Prob. 115RECh. 1 - Prob. 116RECh. 1 - Prob. 117RECh. 1 - Prob. 118RECh. 1 - Prob. 119RECh. 1 - Prob. 120RECh. 1 - Prob. 121RECh. 1 - Prob. 122RECh. 1 - Prob. 123RECh. 1 - Prob. 124RECh. 1 - Prob. 125RECh. 1 - Prob. 126RECh. 1 - Prob. 127RECh. 1 - Prob. 128RECh. 1 - Prob. 129RECh. 1 - Prob. 130RECh. 1 - Prob. 131RECh. 1 - Prob. 132RECh. 1 - Prob. 133RECh. 1 - Prob. 134RECh. 1 - Prob. 135RECh. 1 - Prob. 136RECh. 1 - Prob. 137RECh. 1 - Prob. 138RECh. 1 - Prob. 139RECh. 1 - Prob. 140RECh. 1 - Prob. 141RECh. 1 - Prob. 142RECh. 1 - Prob. 143RECh. 1 - Prob. 144RECh. 1 - Prob. 145RECh. 1 - Prob. 146RECh. 1 - Prob. 147RECh. 1 - Prob. 148RECh. 1 - Prob. 149RECh. 1 - Prob. 150RECh. 1 - Prob. 151RECh. 1 - Prob. 1CTCh. 1 - Prob. 2CTCh. 1 - Prob. 3CTCh. 1 - Prob. 4CTCh. 1 - Prob. 5CTCh. 1 - Prob. 6CTCh. 1 - Prob. 7CTCh. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - Prob. 10CTCh. 1 - Prob. 11CTCh. 1 - Prob. 12CTCh. 1 - Prob. 13CTCh. 1 - Prob. 14CTCh. 1 - Prob. 15CTCh. 1 - Prob. 16CTCh. 1 - Prob. 17CTCh. 1 - Prob. 18CTCh. 1 - Prob. 19CTCh. 1 - Prob. 20CT
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Chain Rule dy:dx = dy:du*du:dx; Author: Robert Cappetta;https://www.youtube.com/watch?v=IUYniALwbHs;License: Standard YouTube License, CC-BY
CHAIN RULE Part 1; Author: Btech Maths Hub;https://www.youtube.com/watch?v=TIAw6AJ_5Po;License: Standard YouTube License, CC-BY