Introduction to Statistics and Data Analysis
5th Edition
ISBN: 9781305115347
Author: Roxy Peck; Chris Olsen; Jay L. Devore
Publisher: Brooks Cole
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13.4, Problem 43E
The article “Performance Test Conducted for a Gas Air-Conditioning System” (American Society of Heating, Refrigerating, and Air Conditioning Engineering [1969]: 54) reported the following data on maximum outdoor temperature (x) and hours of chiller operation per day (y) for a 3-ton residential gas air-conditioning system:
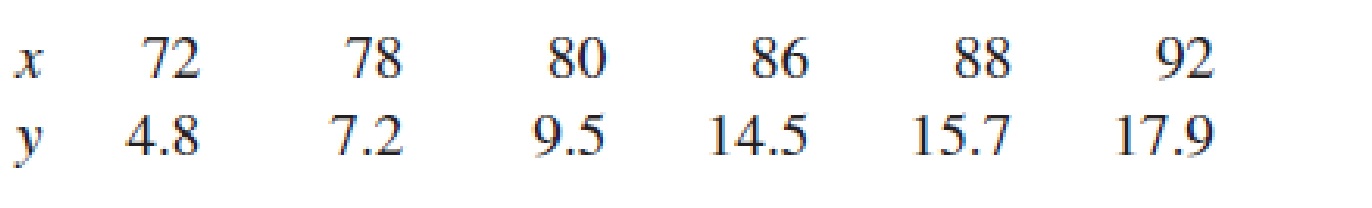
Suppose that the system is actually a prototype model, and the manufacturer does not wish to produce this model unless the data strongly indicate that when maximum outdoor temperature is 82°F. The true average number of hours of chiller operation is less than 12. The appropriate hypotheses are then
H0: α + β(82) = 12 versus Ha: α + β(82) < 12
Use the statistic
which has a t distribution based on (n – 2) df when H0 is true, to test the hypotheses at significance level 0.01.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The output of a solar panel (photovoltaic) system depends on its size. A manufacturer states that the average daily production of its 1.5 kW system is 6.6 kilowatt hours (kWh) for Perth conditions. A consumer group monitored this 1.5 kW system in 20 different Perth homes and measured the average daily production by the systems in these homes over a one month period during October. The data is provided here.
kWh 6.2, 5.8, 5.9, 6.1, 6.4, 6.3, 6.9, 5.5, 7.4, 6.7, 6.3, 6.2, 7.1, 6.8, 5.9, 5.4, 7.2, 6.7, 5.8, 6.9
1. Analyse the consumer group’s data to test if the manufacturer’s claim of an average of 6.6 kWh per day is reasonable. State appropriate hypotheses, assumptions and decision rule at α = 0.10. What conclusions would you report to the consumer group? (Hint: You will need to find Descriptive Statistics first.)
2. If 48 homes in the central Australian city of Alice Springs had this system installed and similar data was collected, in order to assess whether average daily production in…
Apply the predictive control law to a fifth-order process:Y(s)/(s)=1/(5s+1)⁵.Evaluate the effect of tuning paramete rJ on the set-pointresponses for values of J=3, 4, 6, and 8 and Δt=5 min.
Data from the US Department of Energy’s US Energy Information Administration (eia.doe.gov) provides a look at the energy-related carbon dioxide emissions by end use sector (residential, commercial, industrial, transportation) from years 1990 to 2009. (Report # DOE/EIA0573(2009)). Here we would like to see if the CO2 emissions from the Industrial sector are less than that from the Transportation sector. Below are the results:
14. What type of study is this?
a. Paired
b. Two-Sample Independent
15. What type of plot would we use?
a. Histogram of the differences
b. Side-by-side boxplots
c. Pie chart
d. Bar graph
16. Was the HOV/pooled test used above (hint: look at the df)?
YES
NO
17. Is there evidence that the CO2 emissions from the Industrial sector are less than that from the Transportation sector?
YES
NO
18. If we were to test to see if there was a difference between the CO2 emissions from the Industrial sector and the Transportation sector, what would be the p-value? (report to 3…
Chapter 13 Solutions
Introduction to Statistics and Data Analysis
Ch. 13.1 - Prob. 1ECh. 13.1 - The flow rate in a device used for air quality...Ch. 13.1 - The paper Predicting Yolk Height, Yolk Width,...Ch. 13.1 - Prob. 4ECh. 13.1 - Suppose that a simple linear regression model is...Ch. 13.1 - a. Explain the difference between the line y x...Ch. 13.1 - Prob. 7ECh. 13.1 - Hormone replacement therapy (HRT) is thought to...Ch. 13.1 - Prob. 9ECh. 13.1 - A simple linear regression model was used to...
Ch. 13.1 - Consider the accompanying data on x = Advertising...Ch. 13.2 - What is the difference between and b? What is the...Ch. 13.2 - The largest commercial fishing enterprise in the...Ch. 13.2 - Prob. 14ECh. 13.2 - Prob. 15ECh. 13.2 - Prob. 16ECh. 13.2 - An experiment to study the relationship between x...Ch. 13.2 - The paper The Effects of Split Keyboard Geometry...Ch. 13.2 - The authors of the paper Decreased Brain Volume in...Ch. 13.2 - Do taller adults make more money? The authors of...Ch. 13.2 - Researchers studying pleasant touch sensations...Ch. 13.2 - Prob. 22ECh. 13.2 - Prob. 23ECh. 13.2 - Consider the accompanying data on x = Research and...Ch. 13.2 - Prob. 25ECh. 13.2 - In anthropological studies, an important...Ch. 13.3 - The graphs accompanying this exercise are based on...Ch. 13.3 - Prob. 28ECh. 13.3 - Prob. 29ECh. 13.3 - The article Vital Dimensions in Volume Perception:...Ch. 13.3 - Prob. 31ECh. 13.3 - An investigation of the relationship between x =...Ch. 13.4 - Prob. 33ECh. 13.4 - Prob. 34ECh. 13.4 - Prob. 35ECh. 13.4 - Prob. 36ECh. 13.4 - A subset of data read from a graph that appeared...Ch. 13.4 - Prob. 38ECh. 13.4 - Prob. 39ECh. 13.4 - Prob. 40ECh. 13.4 - The shelf life of packaged food depends on many...Ch. 13.4 - For the cereal data of the previous exercise, the...Ch. 13.4 - The article Performance Test Conducted for a Gas...Ch. 13.5 - Prob. 44ECh. 13.5 - Prob. 45ECh. 13.5 - A sample of n = 353 college faculty members was...Ch. 13.5 - Prob. 47ECh. 13.5 - Prob. 48ECh. 13.5 - The accompanying summary quantities for x =...Ch. 13.5 - Prob. 50ECh. 13.5 - Prob. 51ECh. 13.6 - Prob. 52ECh. 13 - Prob. 53CRCh. 13 - Prob. 54CRCh. 13 - Prob. 55CRCh. 13 - The article Photocharge Effects in Dye Sensitized...Ch. 13 - Prob. 57CRCh. 13 - Prob. 58CRCh. 13 - Prob. 59CRCh. 13 - Prob. 60CRCh. 13 - Prob. 61CRCh. 13 - The article Improving Fermentation Productivity...Ch. 13 - Prob. 63CRCh. 13 - Prob. 64CRCh. 13 - Prob. 65CRCh. 13 - Prob. 1CRECh. 13 - Prob. 2CRECh. 13 - Prob. 3CRECh. 13 - Prob. 4CRECh. 13 - Prob. 5CRECh. 13 - The accompanying graphical display is similar to...Ch. 13 - Prob. 7CRECh. 13 - Prob. 8CRECh. 13 - Consider the following data on y = Number of songs...Ch. 13 - Many people take ginkgo supplements advertised to...Ch. 13 - Prob. 11CRECh. 13 - Prob. 12CRECh. 13 - Prob. 13CRECh. 13 - Prob. 14CRECh. 13 - The discharge of industrial wastewater into rivers...Ch. 13 - Many people take ginkgo supplements advertised to...Ch. 13 - It is hypothesized that when homing pigeons are...Ch. 13 - Prob. 18CRE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- HW 8.3 X W HW 8.3- Math 210, section A X webassign.net/web/Student/Assignment-Responses/submit?pos 0&dep 21620509&tags autos... Marketing companies are interested in knowing the population percent of women who make the majority of household purchasing decisions. When designing a study to determine this population proportion, what is the minimum number you would need to survey to be 90% confident that the population proportion is estimated to within O.05? (Round your answer up to the nearest whole number.) women Show My Work (Optional) Submit Answer View Next Question Question 5 of 6 View Previous Question Extension Request My Assignments Home 6 11/ 4)arrow_forwardA) In the screenshot i provided B) Does either explanatory variable improve the fit of the model that uses the other? Use a test statistic for each. Use α=0.05.arrow_forwardThe Norwegian government wants to know whether restricting the opening hours of liquor stores reduces alcohol consumption. Holger, an employee of Statistics Norway, is asked to investigate this research question. He uses panel data for n = 60 municipalities observed in T = 10 time periods. The data set contains information on per capita alcohol consumption (in liters per year) in municipality i in year t (alcoholit) and on the number of hours that liquor stores were open during year t in municipality i (hoursit). Holger estimates by OLS and obtains the following estimation results. regress alcohol Inhours, robust Linear regression alcohol alcoholit Bo + ßiln(hoursit) + Uit B Inhours cons Coef. 5.288235 2.768777 Robust Std. Err. .7486464 5.686286 t 0.49 P>|t| Number of obs = 0.626 R-squared Root MSE alcoholit = Bo+piln(hoursit) + ai + Uit [95% Conf. Interval] -8.398742 0.0745 .9568 a) Test the null hypothesis that B₁ = 0 at a 1% significance level. b) Use the above estimation results to…arrow_forward
- Health care workers who use latex gloves with glove powder on a daily basis are particularly susceptible to developing a latex allergy. Each in a sample of 45 hospital employees who were diagnosed with a latex allergy based on a skin-prick test reported on their exposure to latex gloves. Summary statistics for the number of latex gloves used per week are x = 19.5 and s = 12.1. Complete parts (a) - (d). a. Give a point estimate for the average number of latex gloves used per week by all health care workers with a latex allergy. 19.5 b. Form a 95% confidence interval for the average number of latex gloves used per week by all health care workers with a latex allergy. (Use integers or decimals for any numbers in the expression. Round to two decimal places as needed.)arrow_forwardHealth care workers who use latex gloves with glove powder on a daily basis are particularly susceptible to developing a latex allergy. Each in a sample of 47 hospital employees who were diagnosed with a latex allergy based on a skin-prick test reported on their exposure to latex gloves. Summary statistics for the number of latex gloves used per week are x = 19.7 and s = 12.1. Complete parts (a)-(d). a. Give a point estimate for the average number of latex gloves used per week by all health care workers with a latex allergy. 19.7 b. Form a 95% confidence interval for the average number of latex gloves used per week by all health care workers with a latex allergy. (16.24, 23.16) (Use integers or decimals for any numbers in the expression. Round to two decimal places as needed.) c. Give a practical interpretation of the interval, part (b). OA. One can be 95% confident that the average number of latex gloves used per week by all healthcare workers with latex allergy is greater than the…arrow_forwardThe Journal of Engineering in Industry (Aug. 1993) reported on an automated system designed to replace the cutting tool of a drilling machine at optimum times. To test the system, data were collected over a broad range of materials, drill sizes, drill speeds, and feed rates – called machining conditions. Although a total of 168 different machining conditions were possible, only eight were employed in this study. These are described below: Experiment Workpiece Drill Size (in.) 25 25 Drill Speed (грт) 1250 1800 Feed Rate Material (ipr) .011 .005 1 Cast Iron Cast Iron Steel Steel 25 25 3750 2500 .003 .003 .008 4 Steel 25 .125 .125 2500 Steel Steel 4000 4000 3000 .0065 .009 .010 Steel .125 a. Suppose one (and only one) of the 168 possible machining conditions will detect a flaw in the system. What is the probability that the experiment conducted in the study will detect the system flaw? b. Suppose the system flaw occurs when drilling steel material with a 25-inch drill size at a speed of…arrow_forward
- 1. An article in the ASCE Journal of Energy Engineering (1999, Vol. 125, pp. 59-75) describes a study of the thermal inertia properties of autoclaved aerated concrete used as a building material. Five samples of the material were tested in a structure, and the average interior temperatures (•C) reported were as follows: 23.01, 22.22, 22.04, 22.62, and 22.59. 1.1. Test the hypotheses H0 : µ =22.5 versus H1 :µ + 22.5, using a=0.05. Find the P-value 1.2. Explain how the question could be answered by constructing a two-sided confidence interval on the mean interior temperature. Find the confidence interval.arrow_forwardPLS ANSWERarrow_forwardHealth care workers who use latex gloves with glove powder on a daily basis are particularly susceptible to developing a latex allergy. Each in a sample of 47 hospital employees who were diagnosed with a latex allergy based on a skin-prick test reported on their exposure to latex gloves. Summary statistics for the number of latex gloves used per week are x = 19.3 and s = 12.3. Complete parts (a) - (d). a. Give a point estimate for the average number of latex gloves used per week by all health care workers with a latex allergy. b. Form a 95% confidence interval for the average number of latex gloves used per week by all health care workers with a latex allergy. (Use integers or decimals for any numbers in the expression. Round to two decimal places as needed.) с. Gi a practical interpretation of the interval, part (b). A. One can be 95% confident that latex gloves cause allergies for all who use a number of gloves contained in the interval. B. One can be 95% confident that the average…arrow_forward
- An article in the ACI Materials Journal (Vol. 84, 1987, pp. 213-216) describes several experiments investigating the rodding of concrete to remove trapped air. A 3-inch x 6-inch cylinder was used, and the number of times this rod was used is the design variable. The resulting compressive strength of the concrete specimen is the response. The data are shown in the following table. Compressive Strength (psi) Observations Rodding Level 10 15 20 25 1530 1530 1440 1610 1650 1500 1560 1730 1530 1500 1490 1510 (a) Is there any difference in compressive strength due to the rodding level? Use a = 0.05. Calculate to 2 decimal places for Is there statistical evidence to say that rodding level affects compressive strength? (b) Find to 2 decimal places the P-value for the F-statistic computed in part (a). P-value= (c) Analyze the following residual plots to determine model adequacy, Does the assumption of normality seem reasonable? Does there appear to be an outlier in the data? Does the assumption…arrow_forwardJ 2arrow_forwardAn aircraft company wanted to predict the number of worker-hours necessary to finish the design of a new plane. Relevant explanatory variables were thought to be the plane’s top speed, its weight, and the number of parts it had in common with other models built by the company. A sample of 27 of the company’s planes was taken, and the following model was estimated: y = 0 +11+22+33+ Where y = design effort, in millions of worker-hours 1 = plane’s top speed, in miles per hour 2= plane’s weight, in tons 3 = percentage of parts in common with other models The estimated regression coefficients were as follows: b1 = 0.661 b2 = 0.065 b3 = - 0.018 The total sum of squares and regression sum of squares were found to be as follows: SST = 3.881 and SSR = 3.549 Compute and interpret the coefficient of determination. Compute the error sum of squares. Compute the adjusted coefficient of determination. Compute and interpret the coefficient of multiple correlation.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Statistics 4.1 Point Estimators; Author: Dr. Jack L. Jackson II;https://www.youtube.com/watch?v=2MrI0J8XCEE;License: Standard YouTube License, CC-BY
Statistics 101: Point Estimators; Author: Brandon Foltz;https://www.youtube.com/watch?v=4v41z3HwLaM;License: Standard YouTube License, CC-BY
Central limit theorem; Author: 365 Data Science;https://www.youtube.com/watch?v=b5xQmk9veZ4;License: Standard YouTube License, CC-BY
Point Estimate Definition & Example; Author: Prof. Essa;https://www.youtube.com/watch?v=OTVwtvQmSn0;License: Standard Youtube License
Point Estimation; Author: Vamsidhar Ambatipudi;https://www.youtube.com/watch?v=flqhlM2bZWc;License: Standard Youtube License