Physics, Books a la Carte Edition (5th Edition)
5th Edition
ISBN: 9780134020853
Author: James S. Walker
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 86GP
Predict/Calculate A 3.2-kg mass on a spring oscillates as shown in the displacement-versus-time graph in Figure 13-41. (a) Referring to the graph, at what times between t = 0 and t = 6.0 s does the mass experience a force of maximum magnitude? Explain. (b) Calculate the magnitude of the maximum force exerted on the mass. (c) At what times shown in the graph does the mass experience zero force? Explain. (d) How much force is exerted on the mass at the time t = 0.50 s?
Figure 13-41 Problems 85 and 86
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 13 Solutions
Physics, Books a la Carte Edition (5th Edition)
Ch. 13.1 - If the frequency of an oscillator is halved, by...Ch. 13.2 - Prob. 2EYUCh. 13.3 - An object moves with simple harmonic motion about...Ch. 13.4 - Rank the four massspring systems in Figure 13-15...Ch. 13.5 - The total mechanical energy of an ideal...Ch. 13.6 - Rank the four pendulum systems in Figure 13-25 in...Ch. 13.7 - The amplitude of a damped oscillation decreases...Ch. 13.8 - When you drive a pendulum at a frequency f1, you...Ch. 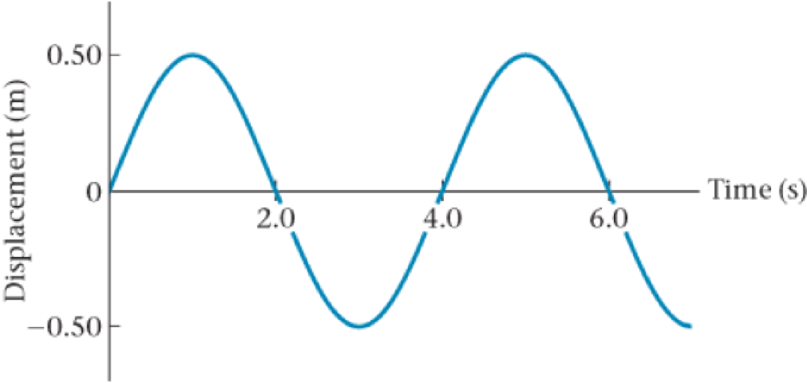13 - A basketball player dribbles a ball with a steady...Ch. 13 - A person rides on a Ferris wheel that rotates with...
Ch. 13 - An air-track cart bounces back and forth between...Ch. 13 - If a mass m and a mass 2m oscillate on identical...Ch. 13 - An object oscillating with simple harmonic motion...Ch. 13 - The position of an object undergoing simple...Ch. 13 - The pendulum bob in Figure 13-18 leaks sand onto...Ch. 13 - A person in a rocking chair completes 12 cycles in...Ch. 13 - While fishing for catfish, a fisherman suddenly...Ch. 13 - If you dribble a basketball with a frequency of...Ch. 13 - You take your pulse and observe 74 heartbeats in a...Ch. 13 - BIO Slow-Motion Dragonfly A frame-by-frame...Ch. 13 - Predict/Calculate (a) Your heart beats with a...Ch. 13 - You rev your cars engine to 3300 rpm (rev/min)....Ch. 13 - A mass moves back and forth in simple harmonic...Ch. 13 - A mass moves back and forth in simple harmonic...Ch. 13 - The position of a mass oscillating on a spring is...Ch. 13 - The position of a mass oscillating on a spring is...Ch. 13 - A position-versus-time plot for an object...Ch. 13 - A mass on a spring oscillates with simple harmonic...Ch. 13 - A mass oscillates on a spring with a period of...Ch. 13 - Predict/Calculate Molecular Oscillations An atom...Ch. 13 - A mass oscillates on a spring with a period T and...Ch. 13 - The position of a mass on a spring is given by x =...Ch. 13 - Predict/Calculate A mass attached to a spring...Ch. 13 - A lawn sprinkler oscillates with simple harmonic...Ch. 13 - A ball rolls on a circular track of radius 0.62 m...Ch. 13 - An object executing simple harmonic motion has a...Ch. 13 - A child rocks back and forth on a porch swing with...Ch. 13 - Predict/Calculate A 30.0-g goldfinch lands on a...Ch. 13 - BIO Tuning Forks in Neurology Tuning forks are...Ch. 13 - A vibrating structural beam in a spacecraft can...Ch. 13 - A peg on a turntable moves with a constant...Ch. 13 - The pistons in an internal combustion engine...Ch. 13 - Vomit Comet NASA trains astronauts to deal with...Ch. 13 - A 0.84-kg air cart is attached to a spring and...Ch. 13 - Predict/Calculate A person rides on a mechanical...Ch. 13 - An object moves with simple harmonic motion of...Ch. 13 - An object executing simple harmonic motion has a...Ch. 13 - Predict/Explain If a mass m is attached to a given...Ch. 13 - Predict/Explain An old car with worn-out shock...Ch. 13 - Predict/Explain The two blocks in Figure 13-34...Ch. 13 - A 0.49-kg mass attached to a spring undergoes...Ch. 13 - A freshly caught catfish is placed on a spring...Ch. 13 - System A consists of a mass m attached to a spring...Ch. 13 - Find the periods of block 1 and block 2 in Figure...Ch. 13 - When a 0.62-kg mass is attached to a vertical...Ch. 13 - A spring with a force constant of 82 N/m is...Ch. 13 - A bunch of grapes is placed in a spring scale at a...Ch. 13 - Two people with a combined mass of 125 kg hop into...Ch. 13 - A 0.95-kg mass attached to a vertical spring of...Ch. 13 - When a 0.184-kg mass is attached to a vertical...Ch. 13 - Predict/Calculate The springs of a 511-kg...Ch. 13 - Predict/Calculate If a mass m is attached to a...Ch. 13 - A 0.285-kg mass is attached to a spring with a...Ch. 13 - A 1.6-kg mass attached to a spring oscillates with...Ch. 13 - Predict/Calculate A 0.40-kg mass is attached to a...Ch. 13 - Prob. 51PCECh. 13 - BIO Astronaut Mass An astronaut uses a Body Mass...Ch. 13 - Predict/Calculate A 0.505-kg block slides on a...Ch. 13 - A 3.55-g bullet embeds itself in a 1.47-kg block,...Ch. 13 - Metronomes, such as the penguin shown in Figure...Ch. 13 - Predict/Explain A grandfather clock keeps correct...Ch. 13 - An observant fan at a baseball game notices that...Ch. 13 - A simple pendulum of length 2.3 m makes 5.0...Ch. 13 - United Nations Pendulum A large pendulum with a...Ch. 13 - Predict/Calculate If the pendulum in the previous...Ch. 13 - A Hula Hoop hangs from a peg. Find the period of...Ch. 13 - A fireman tosses his 0.98-kg hat onto a peg, where...Ch. 13 - Predict/Calculate Consider a meterstick that...Ch. 13 - On the construction site for a new skyscraper, a...Ch. 13 - BIO (a) Find the period of a childs leg as it...Ch. 13 - Suspended from the ceiling of an elevator is a...Ch. 13 - CE An object undergoes simple harmonic motion with...Ch. 13 - CE If the amplitude of a simple harmonic...Ch. 13 - CE A mass m is suspended from the ceiling of an...Ch. 13 - CE A pendulum of length L is suspended from the...Ch. 13 - A 1.3-kg mass is attached to a spring with a force...Ch. 13 - BIO Measuring an Astronauts Mass An astronaut uses...Ch. 13 - Sunspot Observations Sunspots vary in number as a...Ch. 13 - BIO Weighing a Bacterium Scientists are using...Ch. 13 - CE An object undergoing simple harmonic motion...Ch. 13 - The maximum speed of a 4.1-kg mass attached to a...Ch. 13 - The acceleration of a block attached to a spring...Ch. 13 - Helioseismology In 1962, physicists at Cal Tech...Ch. 13 - Predict/Calculate A 9.50-g bullet, moving...Ch. 13 - BIO Spiderweb Oscillations A 1.44-g spider...Ch. 13 - A service dog tag (Figure 13-40) is a circular...Ch. 13 - Calculate the ratio of the kinetic energy to the...Ch. 13 - A 0.340-kg mass slides on a frictionless floor...Ch. 13 - A shock absorber is designed to quickly damp out...Ch. 13 - Predict/Calculate Figure 13-41 shows a...Ch. 13 - Predict/Calculate A 3.2-kg mass on a spring...Ch. 13 - A 0.45-kg crow lands on a slender branch and bobs...Ch. 13 - A mass m is connected to the bottom of a vertical...Ch. 13 - Predict/Calculate Consider the pendulum shown in...Ch. 13 - An object undergoes simple harmonic motion of...Ch. 13 - A physical pendulum consists of a light rod of...Ch. 13 - Predict/Calculate A vertical hollow tube is...Ch. 13 - BIO A Cricket Thermometer, by Jiminy Insects are...Ch. 13 - BIO A Cricket Thermometer, by Jiminy Insects are...Ch. 13 - BIO A Cricket Thermometer, by Jiminy Insects are...Ch. 13 - BIO A Cricket Thermometer, by Jiminy Insects are...Ch. 13 - Predict/Calculate Referring to Example 13-5...Ch. 13 - Predict/Calculate Referring to Example 13-12...Ch. 13 - Predict/Calculate Referring to Example 13-12 (a)...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Sketch the following spectra that would be obtained for 2-chloroethanol: a. The 1H NMR spectrum for an anhydrou...
Organic Chemistry (8th Edition)
18. SCIENTIFIC THINKING By measuring the fossil remains of Homo floresiensis, scientists have estimated its wei...
Campbell Biology: Concepts & Connections (9th Edition)
53. This reaction was monitored as a function of time:
A plot of In[A] versus time yields a straight ...
Chemistry: Structure and Properties (2nd Edition)
Why is an endospore called a resting structure? Of what advantage is an endospore to a bacterial cell?
Microbiology: An Introduction
All of the following processes are involved in the carbon cycle except: a. photosynthesis b. cell respiration c...
Human Biology: Concepts and Current Issues (8th Edition)
Plants use the process of photosynthesis to convert the energy in sunlight to chemical energy in the form of su...
Campbell Essential Biology with Physiology (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A mass is placed on a frictionless, horizontal table. A spring (k=100N/m) , which can be stretched or compressed, is placed on the table. A 5.00-kg mass is attached to one end of the spring, the other end is anchored to the wall. The equilibrium position is marked at zero. A student moves the mass out to x=4.0 cm and releases it from rest. The mass oscillates in SHM. (a) Determine the equations of motion. (b) Find the position, velocity, and acceleration of the mass at time t=3.00 s.arrow_forwardEngineering Application Near the top of the Citigroup Center building in New York City, there is an object with mass of 4.00105kg on springs that have adjustable force constants. Its function is to dampen wind—driven oscillations of the building by oscillating at the same frequency as the building is being driven—the driving force is transferred to the object, which oscillates instead of the entire building. (a) What effective force constant should the springs have to make the object oscillate with a period of 2.00 s? (b) What energy is stored in the springs for a 2.00-m displacement from equilibrium?arrow_forwardIt is important for astronauts in space to monitor their body weight. In Earth orbit, a simple scale only reads an apparent weight of zero, so another method is needed. NASA developed the body mass measuring device (BMMD) for Skylab astronauts. The BMMD is a spring-mounted chair that oscillates in simple harmonic motion (Fig. P16.23). From the period of the motion, the mass of the astronaut can be calculated. In a typical system, the chair has a period of oscillation of 0.901 s when empty. The spring constant is 606 N/m. When a certain astronaut sits in the chair, the period of oscillation increases to 2.37 s. Determine the mass of the astronaut. FIGURE P16.23arrow_forward
- A block with mass m = 0.1 kg oscillates with amplitude .A = 0.1 in at the end of a spring with force constant k = 10 N/m on a frictionless, horizontal surface. Rank the periods of the following situations from greatest to smallest. If any periods are equal, show their equality in your tanking, (a) The system is as described above, (b) The system is as described in situation (a) except the amplitude is 0.2 m. (c) The situation is as described in situation (a) except the mass is 0.2 kg. (d) The situation is as described in situation (a) except the spring has force constant 20 N/m. (e) A small resistive force makes the motion underdamped.arrow_forwardThe mechanical energy of an undamped block-spring system is constant as kinetic energy transforms to elastic potential energy and vice versa. For comparison, explain what happens to the energy of a damped oscillator in terms of the mechanical, potential, and kinetic energies.arrow_forwardReview. A lobstermans buoy is a solid wooden cylinder of radius r and mass M. It is weighted at one end so that it floats upright in calm seawater, having density . A passing shark tugs on the slack rope mooring the buoy to a lobster trap, pulling the buoy down a distance x from its equilibrium position and releasing it. (a) Show that the buoy will execute simple harmonic motion if the resistive effects of the water are ignored. (b) Determine the period of the oscillations.arrow_forward
- Consider the damped oscillator illustrated in Figure 15.19. The mass of the object is 375 g, the spring constant is 100 N/m, and b = 0.100 N s/m. (a) Over what time interval does the amplitude drop to half its initial value? (b) What If? Over what time interval does the mechanical energy drop to half its initial value? (c) Show that, in general, the fractional rate at which the amplitude decreases in a damped harmonic oscillator is one-half the fractional rate at which the mechanical energy decreases.arrow_forwardSome people modify cars to be much closer to the ground than when manufactured. Should they install stiffer springs? Explain your answer.arrow_forwardA blockspring system oscillates with an amplitude of 3.50 cm. The spring constant is 250 N/m and the mass of the block is 0.500 kg. Determine (a) the mechanical energy of the system, (b) the maximum speed of the block, and (c) the maximum acceleration.arrow_forward
- In an engine, a piston oscillates with simpler harmonic motion so that its position varies according to the expression x=5.00cos(2t+6) where x is in centimeters and t is in seconds. At t = O. find (a) the position of the particle, (b) its velocity, and (c) its acceleration. Find (d) the period and (e) the amplitude of the motion.arrow_forwardA horizontal spring attached to a wall has a force constant of 850 N/m. A block of mass 1.00 kg is attached to the spring and oscillates freely on a horizontal, frictionless surface as in Figure 5.22. The initial goal of this problem is to find the velocity at the equilibrium point after the block is released. (a) What objects constitute the system, and through what forces do they interact? (b) What are the two points of interest? (c) Find the energy stored in the spring when the mass is stretched 6.00 cm from equilibrium and again when the mass passes through equilibrium after being released from rest. (d) Write the conservation of energy equation for this situation and solve it for the speed of the mass as it passes equilibrium. Substitute to obtain a numerical value. (e) What is the speed at the halfway point? Why isnt it half the speed at equilibrium?arrow_forwardFigure P13.74 shows a crude model of an insect wing. The mass m represents the entire mass of the wing, which pivots about the fulcrum F. The spring represents the surrounding connective tissue. Motion of the wing corresponds to vibration of the spring. Suppose the mass of the wing is 0.30 g and the effective spring constant of the tissue is 4.7 104 N/m. If the mass m moves up and down a distance of 2.0 mm from its position of equilibrium, what is the maximum speed of the outer tip of the wing? Figure P13.74arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY