
Determine F12 and F21 for the following configurations using the reciprocity theorem and other basic shape factor relations. Do not use tables or charts.
- Long duct
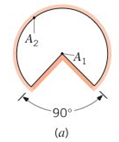


(a)
The shape factors.
Answer to Problem 13.1P
The shape factors are 1 and 0.212.
Explanation of Solution
Formula used:
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Here,
Calculation:
The geometrical shape is given as,
Figure (1)
The above geometry shows that inner surface completely intercepted by the outer surface. Therefore, the value of shape factors can be calculated as,
Conclusion:
Therefore, the shape factors are 1 and 0.212.
(b)
The shape factors.
Answer to Problem 13.1P
The shape factors are 0.5 and 0.25.
Explanation of Solution
Formula used:
The summation rule is given as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Calculation:
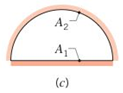
The geometrical shape is given as,
Figure (2)
The above geometry is a convex geometry, therefore the values of shape factor are obtained as,
Further obtaining the values of shape factor by summation rule as,
Further obtaining the values as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Conclusion:
Therefore, the shape factors are 0.5 and 0.25.
(c)
The shape factors.
Answer to Problem 13.1P
The shape factors are 1, 0.637 and 0.363.
Explanation of Solution
Formula used:
The summation rule is given as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
The summation rule is given as,
Calculation:
The geometrical shape is given as,
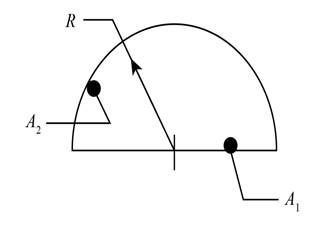
Figure (3)
The above geometry have a flat geometry at bottom, therefore the values of shape factor are obtained as,
Further obtaining the values of shape factor by summation rule as,
The expression for the shape factor for surface 2 with respect to surface 1 can be calculated as,
Further obtain the values of shape factor as,
Conclusion:
Therefore, the shape factors are 1, 0.637 and 0.363
(d)
The shape factors.
Answer to Problem 13.1P
The shape factors are 0.5 and 0.707.
Explanation of Solution
Formula used:
The summation rule is given as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Calculation:
The geometrical shape is given as,
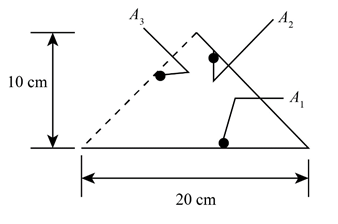
Figure (4)
The above geometry have a flat geometry at bottom, therefore the values of shape factor are obtained as,
Further obtaining the values of shape factor by summation rule as,
The expression for the shape factor for surface 2 with respect to surface 1 can be calculated as,
Conclusion:
Therefore, the shape factors are 0.5 and 0.707.
(e)
The shape factors.
Answer to Problem 13.1P
The shape factors are 0.5 and 0.
Explanation of Solution
Formula used:
The summation rule is given as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Calculation:
The geometrical shape is given as,
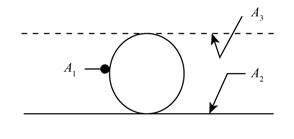
Figure (5)
The above geometry have a flat geometry at bottom, therefore the values of shape factor are obtained as,
Further obtaining the values of shape factor by summation rule as,
The expression for the shape factor for surface 2 with respect to surface 1 can be calculated as,
Conclusion:
Therefore, the shape factors are 0.5 and 0.
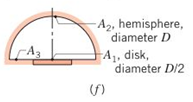
(f)
The shape factors.
Answer to Problem 13.1P
The shape factors are 1 and 0.125.
Explanation of Solution
Formula used:
The summation rule is given as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Calculation:
The geometrical shape is given as,
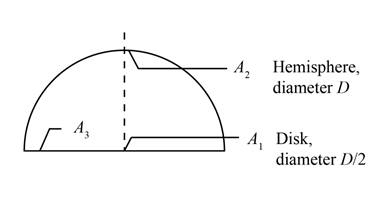
Figure (6)
The above geometry have flat disk surface, therefore the values of shape factor are obtained as,
Further obtaining the values of shape factor by summation rule as,
The expression for the shape factor for surface 2 with respect to surface 1 can be calculated as,
Conclusion:
Therefore, the shape factors are 1 and 0.25.
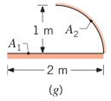
(g)
The shape factors.
Answer to Problem 13.1P
The shape factors are 0.5 and 0.637.
Explanation of Solution
Formula used:
The summation rule is given as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Calculation:
The geometrical shape is given as,
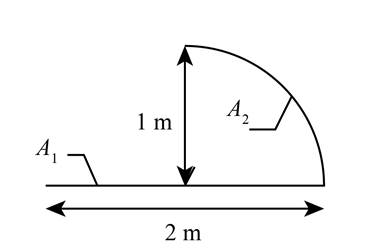
Figure (7)
The above geometry have flat disk surface, therefore the values of shape factor are obtained as,
Further obtaining the values of shape factor by summation rule as,
The expression for the shape factor for surface 2 with respect to surface 1 can be calculated as,
Conclusion:
Therefore, the shape factors are 0.5 and 0.637.
(h)
The shape factors.
Answer to Problem 13.1P
The shape factors are 1 and
Explanation of Solution
Formula used:
The summation rule is given as,
The expression for the shape factor for surface 2 with respect to surface 1 is given as,
Calculation:
The geometrical shape is given as,
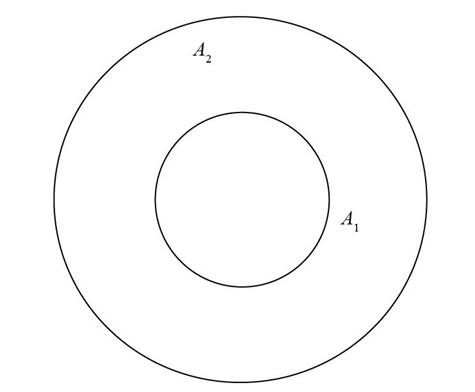
Figure (8)
The above geometry have spherical surface, therefore the values of shape factor are obtained as,
Further obtaining the values of shape factor by summation rule as,
The expression for the shape factor for surface 2 with respect to surface 1 can be calculated as,
Conclusion:
Therefore, the shape factors are 1 and
Want to see more full solutions like this?
Chapter 13 Solutions
Fundamentals of Heat and Mass Transfer
Additional Engineering Textbook Solutions
Vector Mechanics For Engineers
Electric Circuits. (11th Edition)
Thermodynamics: An Engineering Approach
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
Web Development and Design Foundations with HTML5 (8th Edition)
Mechanics of Materials (10th Edition)
- CORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE THANK YOU. CORRECT ANSWER IS ALREADY PROVIDED. I REALLY NEED FBD. The roof truss shown carries roof loads, where P = 10 kN. The truss is consisting of circular arcs top andbottom chords with radii R + h and R, respectively.Given: h = 1.2 m, R = 10 m, s = 2 m.Allowable member stresses:Tension = 250 MPaCompression = 180 MPa1. If member KL has square section, determine the minimum dimension (mm).2. If member KL has circular section, determine the minimum diameter (mm).3. If member GH has circular section, determine the minimum diameter (mm).ANSWERS: (1) 31.73 mm; (2) 35.81 mm; (3) 18.49 mmarrow_forwardPROBLEM 3.23 3.23 Under normal operating condi- tions a motor exerts a torque of magnitude TF at F. The shafts are made of a steel for which the allowable shearing stress is 82 MPa and have diameters of dCDE=24 mm and dFGH = 20 mm. Knowing that rp = 165 mm and rg114 mm, deter- mine the largest torque TF which may be exerted at F. TF F rG- rp B CH TE Earrow_forward1. (16%) (a) If a ductile material fails under pure torsion, please explain the failure mode and describe the observed plane of failure. (b) Suppose a prismatic beam is subjected to equal and opposite couples as shown in Fig. 1. Please sketch the deformation and the stress distribution of the cross section. M M Fig. 1 (c) Describe the definition of the neutral axis. (d) Describe the definition of the modular ratio.arrow_forward
- using the theorem of three moments, find all the moments, I only need concise calculations with minimal explanations. The correct answers are provided at the bottomarrow_forwardMechanics of materialsarrow_forwardusing the theorem of three moments, find all the moments, I need concise calculations onlyarrow_forward
- Can you provide steps and an explaination on how the height value to calculate the Pressure at point B is (-5-3.5) and the solution is 86.4kPa.arrow_forwardPROBLEM 3.46 The solid cylindrical rod BC of length L = 600 mm is attached to the rigid lever AB of length a = 380 mm and to the support at C. When a 500 N force P is applied at A, design specifications require that the displacement of A not exceed 25 mm when a 500 N force P is applied at A For the material indicated determine the required diameter of the rod. Aluminium: Tall = 65 MPa, G = 27 GPa. Aarrow_forwardFind the equivalent mass of the rocker arm assembly with respect to the x coordinate. k₁ mi m2 k₁arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
