Chapter 12.2, Problem 61AYU

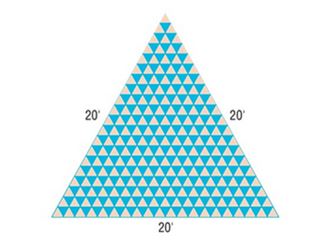
Creating a Mosaic A mosaic is designed in the shape of an equilateral triangle, 20 feet on each side. Each tile in the mosaic is in the shape of an equilateral triangle, 12 inches to a side. The tiles are to alternate in color as shown in the illustration. How many tiles of each color will be required?

To determine

To find: A mosaic is designed in the shape of an equilateral triangle, 20 feet on each side. Each tile in the mosaic is in the shape of an equilateral triangle, 12 inches to a side. The tiles are to alternate in color as shown in the illustration. How many tiles of each color will be required?

Answer to Problem 61AYU

Blue colour $=190$.

Beige colour $=210$.

Explanation of Solution

Given:

A 20 feet mosaic of equilateral triangle is filled with two coloured triangular tiles of 12 inches.

Formula used:

The $n$th term of an arithmetic sequence can be found by the formula

$a_n=a_1+\left(n-1\right)d$   (Formula 1)

Sum of the first $n$ terms of an arithmetic sequence

$S_n=\frac{n}{2}\left[a_1+a_n\right]$   (Formula 2)

Calculation:

From the figure and the given data, the total number of rows is $240/12=20$.

There are two sequences in the problem: one for blue and one for beige.

Sequence for blue coloured tile:

Since Blue coloured tiles start from second row, the total number of rows $=19$.

Therefore the first sequence is $1,2,3\mathrm{...}19$.

Therefore, the total number of blue coloured tiles $=\frac{19}{2}\left[1+\text{ 19}\right]$   (By formula 2)

$=190$

Sequence for beige coloured tile:

Since beige coloured tiles start from first row, the total number of rows $=20$.

Therefore the second sequence is $1,2,3\mathrm{...}20$.

Therefore, the total number of beige coloured tiles $=\frac{20}{2}\left[1+\text{ 20}\right]$   (By formula 2)

$=210$