
Concept explainers
How would you explain the Principle of Mathematical Induction to a friend?
To verify: The principle of Mathematical Induction to a friend.
Answer to Problem 34AYU
The assumption that the given statement is true for in this inductive step is called the inductive hypothesis.
Explanation of Solution
In mathematics, we use a form of complete induction called mathematical induction. To understand the basic principles of mathematical induction, suppose a set of thin rectangular tiles are placed as shown in the figure.
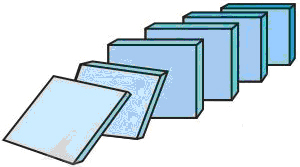
When the first tile is pushed in the indicated direction, all the tiles will fall. To be absolutely sure that all the tiles will fall, it is sufficient to know that
a. The first tile falls, and
b. In the event that any tile falls its successor necessarily falls.
This is the underlying principle of mathematical induction.
We know, the set of natural numbers N is a special ordered subset of the real numbers. In fact, N is the smallest subset of with the following property:
A set is said to be an inductive set if and whenever . Since N is the smallest subset of which is an inductive set, it follows that any subset of that is an inductive set must contain N.
Example: Suppose we wish to find the formula for the sum of positive integers , that is, a formula which will give the value of when , the value , when and so on and suppose that in some manner we are led to believe that the formula is the correct one.
How can this formula actually be proved?
We can, of course, verify the statement for as many positive integral values of n as we like, but this process will not prove the formula for all values of n. What is needed is some kind of chain reaction which will have the effect that once the formula is proved for a particular positive integer the formula will automatically follow for the next positive integer and the next indefinitely. Such a reaction may be considered as produced by the method of mathematical induction
The Principle of Mathematical Induction
Suppose that the following two conditions are satisfied with regard to a statement about natural numbers:
CONDITION I: The statement is true for the natural number 1.
CONDITION II: If the statement is true for some natural number k, it is also true for the next natural number . Then the statement is true for all natural numbers.
Condition I is simply a statement of fact.
There may be situations when a statement is true for all . In this case, step 1 will start from and we shall verify the result for .
Condition II is a conditional property. It does not assert that the given statement is true for , but only that if it is true for , then it is also true for .
So, to prove that the property holds, only prove that conditional proposition: If the statement is true for , then it is also true for .
This is sometimes referred to as the inductive step. The assumption that the given statement is true for in this inductive step is called the inductive hypothesis.
Chapter 12 Solutions
Precalculus Enhanced with Graphing Utilities
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Elementary Statistics
Elementary Statistics: Picturing the World (7th Edition)
- Find a plane containing the point (3, -3, 1) and the line of intersection of the planes 2x + 3y - 3z = 14 and -3x - y + z = −21. The equation of the plane is:arrow_forwardDetermine whether the lines L₁ : F(t) = (−2, 3, −1)t + (0,2,-3) and L2 : ƒ(s) = (2, −3, 1)s + (−10, 17, -8) intersect. If they do, find the point of intersection. ● They intersect at the point They are skew lines They are parallel or equalarrow_forwardAnswer questions 2arrow_forward
- How does a fourier transform works?arrow_forwardDetermine the radius of convergence of a power series:12.6.5, 12.6.6, 12.6.7, 12.6.8Hint: Use Theorem12.5.1 and root test, ratio test, integral testarrow_forwardCan you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forward
- Can you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forwardThere are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three investment? STEP 1: The formula for compound interest is A = nt = P(1 + − − ) n², where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to A = Pert Find r and n for each model, and use these values to write A in terms of t for each case. Annual Model r=0.10 A = Y(t) = 1150 (1.10)* n = 1 Quarterly Model r = 0.10 n = 4 A = Q(t) = 1150(1.025) 4t Continuous Model r=0.10 A = C(t) =…arrow_forwardUse a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forward
- 5. For the function y-x³-3x²-1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (e) determine the intervals of concavity. (d) determine the points of inflection. (e) sketch the graph with the above information indicated on the graph.arrow_forwardCan you solve this 2 question numerical methodarrow_forward1. Estimate the area under the graph of f(x)-25-x from x=0 to x=5 using 5 approximating rectangles Using: (A) right endpoints. (B) left endpoints.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





