
Concept explainers
(a)
To explain: Thereason for the circumference of the base of the cone is
(a)
Answer to Problem 55E
The circumference of the base of the cone is
Explanation of Solution
Given information:A sector of arc length x is cut out from a circular piece of paper with radius 4 in to formed a cone with radius r and height h as shown below.
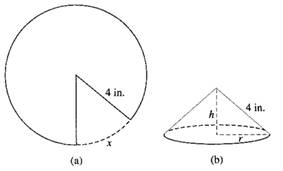
Figure (1)
Calculation:
The formula for the circumference of a circle with radius r is:
Substitute 4 for r in the above formula to find the circumference of given circle,
It is given that the circumference of the base of the cone is
A sector of arc length x is cut out from the circle to form the cone. So, the circumference of the base of the cone is the arc length of sector subtracted from the circumference of the circle.
Therefore, the circumference of the base of the cone is
(b)
To express: The radius of the cone as a function of x .
(b)
Answer to Problem 55E
The radius as a function of x can be written as
Explanation of Solution
Given information: A sector of arc length x is cut out from a circular piece of paper with radius 4 in to formed a cone with radius r and height h as shown below.
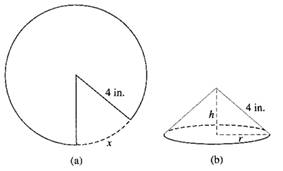
Figure (1)
Calculation:
It is given that the circumference of the base of the cone is
The formula for the circumference of a circle with radius r is:
Substitute
Therefore, the radius as a function of x can be written as
(c)
To express: The height h of the cone as a function of x .
(c)
Answer to Problem 55E
The height h of the cone as a function x can be written as
Explanation of Solution
Given information: A sector of arc length x is cut out from a circular piece of paper with radius 4 in to formed a cone with radius r and height h as shown below.
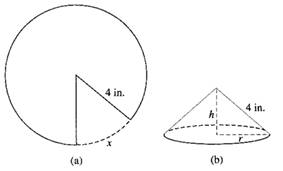
Figure (1)
Calculation:
From part (b), the radius as a function of x can be written as
The formula for the slant height l of a cone is:
Substitute 4 for land
Further simplify.
Therefore, the height h of the cone as a function x can be written as
(c)
To express: The volume V of the cone as a function of x .
(c)
Answer to Problem 55E
The volumeV of the cone as a function x can be written as
Explanation of Solution
Given information: A sector of arc length x is cut out from a circular piece of paper with radius 4 in to formed a cone with radius r and height h as shown below.
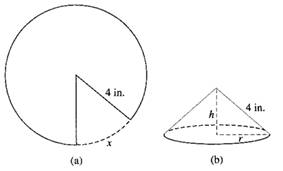
Figure (1)
Calculation:
From part (b), the radius of the cone is
The formula for the volumeV of a cone is:
Substitute
Therefore, the volume V of the cone as a function x can be written as
Chapter 1 Solutions
Calculus: Graphical, Numerical, Algebraic
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
Elementary Statistics (13th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Introductory Statistics
Pre-Algebra Student Edition
University Calculus: Early Transcendentals (4th Edition)
- (10 points) Let f(x, y, z) = ze²²+y². Let E = {(x, y, z) | x² + y² ≤ 4,2 ≤ z ≤ 3}. Calculate the integral f(x, y, z) dv. Earrow_forward(12 points) Let E={(x, y, z)|x²+ y² + z² ≤ 4, x, y, z > 0}. (a) (4 points) Describe the region E using spherical coordinates, that is, find p, 0, and such that (x, y, z) (psin cos 0, psin sin 0, p cos) € E. (b) (8 points) Calculate the integral E xyz dV using spherical coordinates.arrow_forward(10 points) Let f(x, y, z) = ze²²+y². Let E = {(x, y, z) | x² + y² ≤ 4,2 ≤ z < 3}. Calculate the integral y, f(x, y, z) dV.arrow_forward
- (14 points) Let f: R3 R and T: R3. →R³ be defined by f(x, y, z) = ln(x²+ y²+2²), T(p, 0,4)=(psin cos 0, psin sin, pcos). (a) (4 points) Write out the composition g(p, 0, 4) = (foT)(p,, ) explicitly. Then calculate the gradient Vg directly, i.e. without using the chain rule. (b) (4 points) Calculate the gradient Vf(x, y, z) where (x, y, z) = T(p, 0,4). (c) (6 points) Calculate the derivative matrix DT(p, 0, p). Then use the Chain Rule to calculate Vg(r,0,4).arrow_forward(10 points) Let S be the upper hemisphere of the unit sphere x² + y²+2² = 1. Let F(x, y, z) = (x, y, z). Calculate the surface integral J F F-dS. Sarrow_forward(8 points) Calculate the following line integrals. (a) (4 points) F Fds where F(x, y, z) = (x, y, xy) and c(t) = (cost, sint, t), tЄ [0,π] . (b) (4 points) F. Fds where F(x, y, z) = (√xy, e³, xz) where c(t) = (t², t², t), t = [0, 1] .arrow_forward
- review help please and thank you!arrow_forward(10 points) Let S be the surface that is part of the sphere x² + y²+z² = 4 lying below the plane 2√3 and above the plane z-v -√3. Calculate the surface area of S.arrow_forward(8 points) Let D = {(x, y) | 0 ≤ x² + y² ≤4}. Calculate == (x² + y²)³/2dA by making a change of variables to polar coordinates, i.e. x=rcos 0, y = r sin 0.arrow_forward
- x² - y² (10 points) Let f(x,y): = (a) (6 points) For each vector u = (1, 2), calculate the directional derivative Duƒ(1,1). (b) (4 points) Determine all unit vectors u for which Duf(1, 1) = 0.arrow_forwardSolve : X + sin x = 0. By the false positioning numerical methodarrow_forwardSolve: X + sin X = 0 by the false positionining numerical methodarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





