
To match: The parametric equations with its appropriate graph, write the approximate dimensions of the viewing window and a parameter interval that traces the curve exactly once.
Answer to Problem 4E
The correct match of the graph for given parametric equation is (b), the dimension of the window is
Explanation of Solution
Given information: The parametric equations are
Calculation:
Use the following step to graph the parametric equations by graphing calculator.
Step 1: Press the
Step 2: Press
Step 3: Press
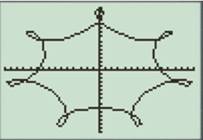
Figure (1)
First find the starting point at
Substitute 0 for
Substitute 0 for
Find the next value of
Substitute
Substitute
The interval is
Therefore, the correct match of the graph for given parametric equation is (b), the dimension of the window is
Chapter 1 Solutions
Calculus: Graphical, Numerical, Algebraic
Additional Math Textbook Solutions
Pre-Algebra Student Edition
College Algebra with Modeling & Visualization (5th Edition)
Introductory Statistics
Elementary Statistics (13th Edition)
Basic Business Statistics, Student Value Edition
- 39. (a) Show that Σeak converges for each α > 0. (b) Show that keak converges for each a > 0. k=0 (c) Show that, more generally, Σk"eak converges for each k=0 nonnegative integer n and each a > 0.arrow_forward#3 Find the derivative y' = of the following functions, using the derivative rules: dx a) y-Cos 6x b) y=x-Sin4x c) y=x-Cos3x d) y=x-R CD-X:-:TCH :D:D:D - Sin f) Sin(x²) (9) Tan (x³)arrow_forwardmate hat is the largest area that can be en 18 For the function y=x³-3x² - 1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (c) determine the intervals of concavity. (d) determine the points of inflection. b) (e) sketch the graph with the above information indicated on the graph.arrow_forward
- use L'Hopital Rule to evaluate the following. a) 4x3 +10x2 23009׳-9 943-9 b) hm 3-84 хто бу+2 < xan x-30650)arrow_forwardEvaluate the next integralarrow_forward1. For each of the following, find the critical numbers of f, the intervals on which f is increasing or decreasing, and the relative maximum and minimum values of f. (a) f(x) = x² - 2x²+3 (b) f(x) = (x+1)5-5x-2 (c) f(x) = x2 x-9 2. For each of the following, find the intervals on which f is concave upward or downward and the inflection points of f. (a) f(x) = x - 2x²+3 (b) g(x) = x³- x (c) f(x)=x-6x3 + x-8 3. Find the relative maximum and minimum values of the following functions by using the Second Derivative Test. (a) f(x)=1+3x² - 2x3 (b) g(x) = 2x3 + 3x² - 12x-4arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





