Vector Mechanics for Engineers: Statics and Dynamics
11th Edition
ISBN: 9780073398242
Author: Ferdinand P. Beer, E. Russell Johnston Jr., David Mazurek, Phillip J. Cornwell, Brian Self
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 11.5, Problem 11.160P
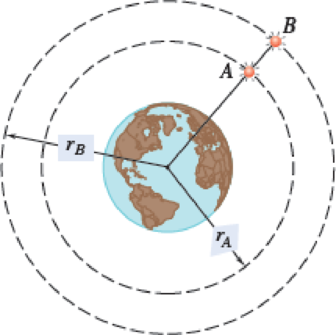
Satellites A and B are traveling in the same plane in circular orbits around the earth at altitudes of 120 and 200 mi, respectively. If at t = 0 the satellites are aligned as shown and knowing that the radius of the earth is R = 3960 mi, determine when the satellites will next be radially aligned. (See the information given in Probs. 11.153 and 11.154.)
Fig. P11.160
11.153 and 11.154 A satellite will travel indefinitely in a circular orbit around a planet if the normal component of the acceleration of the satellite is equal to g(R/r)2, where g is the acceleration of gravity at the surface of the planet, R is the radius of the planet, and r is the distance from the center of the planet to the satellite. Knowing that the diameter of the sun is 1.39 Gm and that the acceleration of gravity at its surface is 274 m/s2, determine the radius of the orbit of the indicated planet around the sun assuming that the orbit is circular.
11.153 Earth: (vmean)orbit = 107 Mm/h.
11.154 Saturn: (vmean)orbit = 34.7 Mm/h.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
-6-
8 من 8
Mechanical vibration
HW-prob-1
lecture 8 By: Lecturer Mohammed O. attea
The 8-lb body is released from rest a distance xo
to the right of the equilibrium position.
Determine the displacement x as a function of time t,
where t = 0 is the time of release.
c=2.5 lb-sec/ft
wwwww
k-3 lb/in.
8 lb
Prob. -2
Find the value of (c) if the system is critically
damping.
Prob-3
Find Meq and Ceq at point B, Drive eq. of
motion for the system below.
Ш
H
-7~
+
目
T T & T
тт
+
Q For the following plan of building foundation, Determine
immediate settlement at points (A) and (B) knowing that: E,-25MPa,
u=0.3, Depth of foundation (D) =1m, Depth of layer below base level
of foundation (H)=10m.
3m
2m
100kPa
A
2m
150kPa
5m
200kPa
B
W
PE
2
43
R² 80 + 10 + kr³ Ø8=0 +0
R²+J+ kr200
R² + J-) + k r² = 0
kr20
kr20
8+
W₁ =
= 0
R²+1)
R²+J+)
4
lec 8.pdf
Mechanical vibration
lecture 6
By: Lecturer Mohammed C. Attea
HW1 (Energy method)
Find equation of motion and natural frequency for the system shown in fig. by energy
method.
m. Jo
000
HW2// For the system Fig below find
1-F.B.D
2Eq.of motion
8 wn
4-0 (1)
-5-
m
Chapter 11 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
Ch. 11.1 - A bus travels the 100 miles between A and B at 50...Ch. 11.1 - Two cars A and B race each other down a straight...Ch. 11.1 - A snowboarder starts from rest at the top of a...Ch. 11.1 - Prob. 11.2PCh. 11.1 - Prob. 11.3PCh. 11.1 - A loaded railroad car is rolling at a constant...Ch. 11.1 - Prob. 11.5PCh. 11.1 - Prob. 11.6PCh. 11.1 - A girl operates a radio-controlled model car in a...Ch. 11.1 - The motion of a particle is defined by the...
Ch. 11.1 - The brakes of a car are applied, causing it to...Ch. 11.1 - The acceleration of a particle is defined by the...Ch. 11.1 - Prob. 11.11PCh. 11.1 - Prob. 11.12PCh. 11.1 - A Scotch yoke is a mechanism that transforms the...Ch. 11.1 - For the Scotch yoke mechanism shown, the...Ch. 11.1 - Prob. 11.15PCh. 11.1 - Prob. 11.16PCh. 11.1 - Prob. 11.17PCh. 11.1 - A brass (nonmagnetic) block A and a steel magnet B...Ch. 11.1 - Based on experimental observations, the...Ch. 11.1 - A spring AB is attached to a support at A and to a...Ch. 11.1 - Prob. 11.21PCh. 11.1 - Prob. 11.22PCh. 11.1 - A ball is dropped from a boat so that it strikes...Ch. 11.1 - The acceleration of a particle is defined by the...Ch. 11.1 - The acceleration of a particle is defined by the...Ch. 11.1 - A human-powered vehicle (HPV) team wants to model...Ch. 11.1 - Prob. 11.27PCh. 11.1 - Based on observations, the speed of a jogger can...Ch. 11.1 - The acceleration due to gravity at an altitude y...Ch. 11.1 - The acceleration due to gravity of a particle...Ch. 11.1 - The velocity of a particle is v = v0[1 sin(t/T)]....Ch. 11.1 - An eccentric circular cam, which serves a similar...Ch. 11.2 - 11.33 An airplane begins its take-off run at A...Ch. 11.2 - Prob. 11.34PCh. 11.2 - Steep safety ramps are built beside mountain...Ch. 11.2 - A group of students launches a model rocket in the...Ch. 11.2 - A small package is released from rest at A and...Ch. 11.2 - A sprinter in a 100-m race accelerates uniformly...Ch. 11.2 - Automobile A starts from O and accelerates at the...Ch. 11.2 - In a boat race, boat A is leading boat B by 50 m...Ch. 11.2 - As relay runner A enters the 65-ft-long exchange...Ch. 11.2 - Automobiles A and B are traveling in adjacent...Ch. 11.2 - Two automobiles A and B are approaching each other...Ch. 11.2 - An elevator is moving upward at a constant speed...Ch. 11.2 - Prob. 11.45PCh. 11.2 - Prob. 11.46PCh. 11.2 - The elevator E shown in the figure moves downward...Ch. 11.2 - The elevator E shown starts from rest and moves...Ch. 11.2 - An athlete pulls handle A to the left with a...Ch. 11.2 - An athlete pulls handle A to the left with a...Ch. 11.2 - Prob. 11.51PCh. 11.2 - Prob. 11.52PCh. 11.2 - A farmer lifts his hay bales into the top loft of...Ch. 11.2 - The motor M reels in the cable at a constant rate...Ch. 11.2 - Collar A starts from rest at t = 0 and moves...Ch. 11.2 - Prob. 11.56PCh. 11.2 - Block B starts from rest, block A moves with a...Ch. 11.2 - Prob. 11.58PCh. 11.2 - The system shown starts from rest, and each...Ch. 11.2 - Prob. 11.60PCh. 11.3 - A particle moves in a straight line with a...Ch. 11.3 - Prob. 11.62PCh. 11.3 - A particle moves in a straight line with the...Ch. 11.3 - A particle moves in a straight line with the...Ch. 11.3 - A particle moves in a straight line with the...Ch. 11.3 - Prob. 11.66PCh. 11.3 - A commuter train traveling at 40 mi/h is 3 mi from...Ch. 11.3 - Prob. 11.68PCh. 11.3 - In a water-tank test involving the launching of a...Ch. 11.3 - The acceleration record shown was obtained for a...Ch. 11.3 - Prob. 11.71PCh. 11.3 - Prob. 11.72PCh. 11.3 - Prob. 11.73PCh. 11.3 - Car A is traveling on a highway at a constant...Ch. 11.3 - Prob. 11.75PCh. 11.3 - Prob. 11.76PCh. 11.3 - Prob. 11.77PCh. 11.3 - Prob. 11.78PCh. 11.3 - An airport shuttle train travels between two...Ch. 11.3 - Prob. 11.80PCh. 11.3 - Prob. 11.81PCh. 11.3 - The acceleration record shown was obtained during...Ch. 11.3 - Prob. 11.83PCh. 11.3 - Prob. 11.84PCh. 11.3 - An elevator starts from rest and rises 40 m to its...Ch. 11.3 - Two road rally checkpoints A and B are located on...Ch. 11.3 - As shown in the figure, from t = 0 to t = 4 s, the...Ch. 11.3 - Prob. 11.88PCh. 11.4 - Two model rockets are fired simultaneously from a...Ch. 11.4 - Ball A is thrown straight up. Which of the...Ch. 11.4 - Ball A is thrown straight up with an initial speed...Ch. 11.4 - Two cars are approaching an intersection at...Ch. 11.4 - Prob. 11.7CQCh. 11.4 - A ball is thrown so that the motion is defined by...Ch. 11.4 - The motion of a vibrating particle is defined by...Ch. 11.4 - Prob. 11.91PCh. 11.4 - The motion of a particle is defined by the...Ch. 11.4 - Prob. 11.93PCh. 11.4 - A girl operates a radio-controlled model car in a...Ch. 11.4 - The three-dimensional motion of a particle is...Ch. 11.4 - The three-dimensional motion of a particle is...Ch. 11.4 - Prob. 11.97PCh. 11.4 - A ski jumper starts with a horizontal take-off...Ch. 11.4 - A baseball pitching machine throws baseballs with...Ch. 11.4 - While delivering newspapers, a girl throws a...Ch. 11.4 - Prob. 11.101PCh. 11.4 - In slow pitch softball, the underhand pitch must...Ch. 11.4 - A volleyball player serves the ball with an...Ch. 11.4 - Prob. 11.104PCh. 11.4 - A homeowner uses a snowblower to clear his...Ch. 11.4 - At halftime of a football game, souvenir balls are...Ch. 11.4 - A basketball player shoots when she is 16 ft from...Ch. 11.4 - A tennis player serves the ball at a height h =...Ch. 11.4 - Prob. 11.109PCh. 11.4 - While holding one of its ends, a worker lobs a...Ch. 11.4 - Prob. 11.111PCh. 11.4 - Prob. 11.112PCh. 11.4 - Prob. 11.113PCh. 11.4 - A worker uses high-pressure water to clean the...Ch. 11.4 - An oscillating garden sprinkler which discharges...Ch. 11.4 - A nozzle at A discharges water with an initial...Ch. 11.4 - The velocities of skiers A and B are as shown....Ch. 11.4 - The three blocks shown move with constant...Ch. 11.4 - Three seconds after automobile B passes through...Ch. 11.4 - Prob. 11.120PCh. 11.4 - Airplanes A and B are flying at the same altitude...Ch. 11.4 - Prob. 11.122PCh. 11.4 - Prob. 11.123PCh. 11.4 - Prob. 11.124PCh. 11.4 - A boat is moving to the right with a constant...Ch. 11.4 - Prob. 11.126PCh. 11.4 - Prob. 11.127PCh. 11.4 - Conveyor belt A, which forms a 20 angle with the...Ch. 11.4 - During a rainstorm, the paths of the raindrops...Ch. 11.4 - Prob. 11.130PCh. 11.4 - Prob. 11.131PCh. 11.4 - As part of a department store display, a model...Ch. 11.5 - The Ferris wheel is rotating with a constant...Ch. 11.5 - Prob. 11.9CQCh. 11.5 - A child walks across merry-go-round A with a...Ch. 11.5 - Prob. 11.133PCh. 11.5 - Determine the maximum speed that the cars of the...Ch. 11.5 - Prob. 11.135PCh. 11.5 - The diameter of the eye of a stationary hurricane...Ch. 11.5 - The peripheral speed of the tooth of a...Ch. 11.5 - A robot arm moves so that P travels in a circle...Ch. 11.5 - A monorail train starts from rest on a curve of...Ch. 11.5 - Prob. 11.140PCh. 11.5 - Race car A is traveling on a straight portion of...Ch. 11.5 - At a given instant in an airplane race, airplane A...Ch. 11.5 - A race car enters the circular portion of a track...Ch. 11.5 - Prob. 11.144PCh. 11.5 - A golfer hits a golf ball from point A with an...Ch. 11.5 - Prob. 11.146PCh. 11.5 - Coal is discharged from the tailgate A of a dump...Ch. 11.5 - From measurements of a photograph, it has been...Ch. 11.5 - A child throws a ball from point A with an initial...Ch. 11.5 - A projectile is fired from point A with an initial...Ch. 11.5 - Prob. 11.151PCh. 11.5 - Prob. 11.152PCh. 11.5 - 11.153 and 11.154 A satellite will travel...Ch. 11.5 - Prob. 11.154PCh. 11.5 - Prob. 11.155PCh. 11.5 - Prob. 11.156PCh. 11.5 - Prob. 11.157PCh. 11.5 - A satellite will travel indefinitely in a circular...Ch. 11.5 - Knowing that the radius of the earth is 6370 km,...Ch. 11.5 - Satellites A and B are traveling in the same plane...Ch. 11.5 - 11.162 The path of a particle P is a limaçon. The...Ch. 11.5 - During a parasailing ride, the boat is traveling...Ch. 11.5 - Some parasailing systems use a winch to pull the...Ch. 11.5 - As rod OA rotates, pin P moves along the parabola...Ch. 11.5 - The pin at B is free to slide along the circular...Ch. 11.5 - Prob. 11.167PCh. 11.5 - After taking off, a helicopter climbs in a...Ch. 11.5 - At the bottom of a loop in the vertical plane, an...Ch. 11.5 - Prob. 11.170PCh. 11.5 - Prob. 11.171PCh. 11.5 - Prob. 11.172PCh. 11.5 - 11.173 and 11.174 A particle moves along the...Ch. 11.5 - Prob. 11.174PCh. 11.5 - Prob. 11.175PCh. 11.5 - Prob. 11.176PCh. 11.5 - Prob. 11.177PCh. 11.5 - Prob. 11.178PCh. 11.5 - Prob. 11.179PCh. 11.5 - For the conic helix of Prob. 11.95, determine the...Ch. 11 - Prob. 11.182RPCh. 11 - A drag racing car starts from rest and moves down...Ch. 11 - Prob. 11.184RPCh. 11 - The velocities of commuter trains A and B are as...Ch. 11 - Knowing that slider block A starts from rest and...Ch. 11 - Prob. 11.187RPCh. 11 - A golfer hits a ball with an initial velocity of...Ch. 11 - As the truck shown begins to back up with a...Ch. 11 - A velodrome is a specially designed track used in...Ch. 11 - Sand is discharged at A from a conveyor belt and...Ch. 11 - The end point B of a boom is originally 5 m from...Ch. 11 - A telemetry system is used to quantify kinematic...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The hose supplying the cylinder operating the bucket of a large excavator has fluid at 1000 psi flowing at 5 gpm. What is theavailable power in the line?arrow_forwardQ For the following plan of building foundation, Determine immediate settlement at points (A) and (B) knowing that: E,-25MPa, u=0.3, Depth of foundation (D) =1m, Depth of layer below base level of foundation (H)=10m. 3m 2m 100kPa A 2m 150kPa 5m 200kPa Barrow_forwardGiven the following data for crack rocker mechanism. If θ2 = 4π/3 and ω2 = 1 rad/s, Determine all possible values of ω4 and ω3 analytically. The lengths of links are a = 2, b = 8, c = 7 and d = 9 in cm.arrow_forward
- Q6] (20 Marks) Select the most suitable choice for the following statements: modo digi -1A 10 af5 1 -The copper-based alloy which is responded to age hardening is a) copper-nickel b) aluminum bronze c) copper - beryllium d) brass besincaluy 2- Highly elastic polymers may experience elongations to greater than.... b) 500% bromsia-P c) 1000%. d) 1200% 15m or -2 a)100% 3- The cooling rate of quenching the steel in saltwater will be ......the cooling rate of quenching ir c) faster than sold) none of them a) slower than 4- Adding of a) Cr b) the same as ...... Will lead to stabilize the b) Mo 10 austenite in steel. c) Nimble avolls 1d) Sized loloin nl 5- The adjacent linear chains of crosslinked polymers are joined one to another at various positic DIR... by.........bonds c) covalent noisqo gd) ionic lg 120M 6- For the ceramic with coordination number 6 the cation to anion radius ratio will be a) Van der Waals a) 0.155-0.225 a) linear b) hydrogen (b) 0.225-0.414 c) 0.414 0.732 ..polymers.…arrow_forwardExamine Notes: Attempt Six Questions Only. rever necessa , Q1] (20 Marks) Answer with true (T) or false (F), corrects the wrong phrases, and gives sho reasons for correct and corrected statements: 1- High chromium irons are basically grey cast irons alloyed with 12 to 30 % Cr. yous board-19qgo orT-1 2- The drawbacks of Al- Li alloys are their high young modulus and high density.&M 0) (0 3- Vulcanized rubbers are classified under thermoplastic polymers. 4- Diamond is a stable carbon polymorph at room temperature and atmospheric pressure. ( 5- The metallic ions of ceramic are called anions, and they are positively charged. yldgiH-S 69001(6arrow_forwardH.W 5.4 Calculate the load that will make point A move to the left by 6mm, E-228GPa. The diameters of the rods are as shown in fig. below. 2P- PA 50mm B 200mm 2P 0.9m 1.3marrow_forward
- d₁ = = Two solid cylindrical road AB and BC are welded together at B and loaded as shown. Knowing that 30mm (for AB) and d₂ 50mm (for BC), find the average normal stress in each road and the total deformation of road AB and BC. E=220GPa H.W 5.3 60kN A For the previous example calculate the value of force P so that the point A will not move, and what is the total length of road AB at that force? P◄ A 125kN 125kN 0.9m 125kN 125kN 0.9m B B 1.3m 1.3marrow_forwardClass: B Calculate the load that will make point A move to the left by 6mm, E-228GPa The cross sections of the rods are as shown in fig. below. 183 P- Solution 1.418mm 200mm 80mm 3P- 18.3 A 080mm B 200mm 3P- 0.9m إعدادات العرض 1.3m 4.061mmarrow_forwardH.W6 Determine the largest weight W that can be supported by two wires shown in Fig. P109. The stress in either wire is not to exceed 30 ksi. The cross- sectional areas of wires AB and AC are 0.4 in2 and 0.5 in2, respectively. 50° 30° Warrow_forward
- Find equation of motion and natural frequency for the system shown in fig. by energy method. H.W2// For the system Fig below find 1-F.B.D 2-Eq.of motion 8wn 4-0 (5) m. Jo marrow_forward2. Read the following Vernier caliper measurements. (The scales have been enlarged for easier reading.) The Vernier caliper is calibrated in metric units. (a) 0 1 2 3 4 5 سلسلسله (b) 1 2 3 4 5 6 سلسل (c) 1 23456 (d) 1 2 3 4 5 6 سلسلسarrow_forwardExplain why on the interval 0<x<1000 mm and 1000<x<2000mm, Mt is equal to positive 160 Nm, but at x= 0mm and x=1000mm Mt is equal to -160 Nm (negative value!). What is the reason for the sign change of Mt?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Dynamics - Lesson 1: Introduction and Constant Acceleration Equations; Author: Jeff Hanson;https://www.youtube.com/watch?v=7aMiZ3b0Ieg;License: Standard YouTube License, CC-BY