Chapter 11.3, Problem 26PPS

a.

To determine

To graph: A circular graph of diameter 2 in. with the given data.

Explanation of Solution

Given information: Diameter of the circle is 2 in. and the table of the results of a survey of students is as follows,

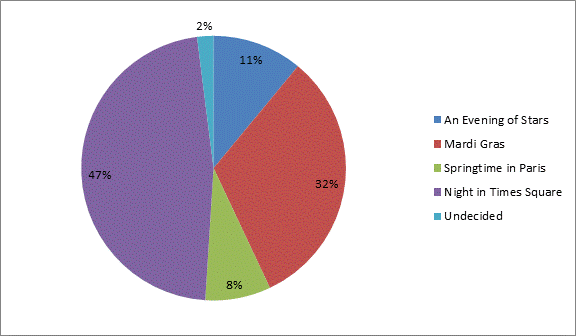
Theme	Percent
An Evening of Stars	11
Mardi Gras	32
Springtime in Paris	8
Night in Times Square	47
Undecided	2

Calculation: For the graph angle of each sector of different themes is required.

So, angle of the sector of,

An Evening of Stars $=360\times \frac{11}{100}={39.6}^{\circ }$

Mardi Gras $=360\times \frac{32}{100}={115.2}^{\circ }$

Springtime in Paris $=360\times \frac{8}{100}={28.8}^{\circ }$

Night in Times Square $=360\times \frac{47}{100}={169.2}^{\circ }$

Undecided $=360\times \frac{2}{100}={7.2}^{\circ }$

Graph:

  

b.

To determine

To calculate: Area of each theme’s sector of the graph.

Answer to Problem 26PPS

The area of the sector of An Evening of Stars is 0.34 in², Mardi Gras is 1.00 in², Springtime in Paris is 0.25 in², Night in Times Square is 1.47 in² and Undecided is 0.06 in².

Explanation of Solution

Given information: Diameter of the circle is 2 in. and the table of the results of a survey of students is as follows,

Theme	Percent
An Evening of Stars	11
Mardi Gras	32
Springtime in Paris	8
Night in Times Square	47
Undecided	2

Formula used: Area of sector $=\mathrm{\pi }{\mathrm{r}}^2\times$ Percentage portion of sector

  $\mathrm{r}=$ Radius of the circle.

Calculation:

Here, $\mathrm{r}=\frac{2}{2}=1$ and $\mathrm{\pi }=\frac{22}{7}$

Area of the sector of,

An Evening of Stars $=\frac{22}{7}\times 1^2\times \frac{11}{100}=0.34$ in²

Mardi Gras $=\frac{22}{7}\times 1^2\times \frac{32}{100}=1.00$ in²

Springtime in Paris $=\frac{22}{7}\times 1^2\times \frac{8}{100}=0.25$ in²

Night in Times Square $=\frac{22}{7}\times 1^2\times \frac{47}{100}=1.47$ in²

Undecided $=\frac{22}{7}\times 1^2\times \frac{2}{100}=0.06$ in²

Hence, the area of the sector of An Evening of Stars is 0.34 in², Mardi Gras is 1.00 in², Springtime in Paris is 0.25 in², Night in Times Square is 1.47 in² and Undecided is 0.06 in².