
Concept explainers
a.
To calculate: The equation of the perimeter and the area of rectangle with the given information.
a.
Answer to Problem 36PPS
The equation of the perimeter of the rectangle is
Explanation of Solution
Given information: The perimeter of a rectangle is 12 units and length of the rectangle is x and the width of the rectangle is y.
Formula used:
The perimeter and area of a rectangle is given by
Calculation:
The given information is:
Hence, the equation of the perimeter of the given rectangle is
The equation of the area of the given rectangle is
Therefore, the equation of the perimeter of the rectangle is
b.
To calculate: All the possible whole-number values that satisfies as the length and width of the rectangle and to find the area of the rectangle for each pair.
b.
Answer to Problem 36PPS
The possible values of x & y and the area associated with them is given below in the tabular form.
Explanation of Solution
Given information: The perimeter of a rectangle is 12 units and length of the rectangle is x and the width of the rectangle is y.
Formula used:
The perimeter and area of a rectangle is given by
Calculation:
By using the results of equation (1) & (2)
The equation of the perimeter of the rectangle is
The equation of the area of the rectangle is
Here for different values of x & y satisfying equation (1), there will be different value of the area of the rectangle.
Also since x is the length of the rectangle so it cannot be less than 1 and it cannot be more than 5 because then y will be zero which is also not possible as it is the width of the rectangle, hence
Therefore the possible values of x & y and the area associated with them is given below in the tabular form.
c.
To graph: The area of the rectangle with respect to the length of the rectangle.
c.
Explanation of Solution
Given information: By using the result of part-b, the variation of area with the value of x & y is given below.
Graph:
The graph of area with respect to the length of the rectangle is given below.
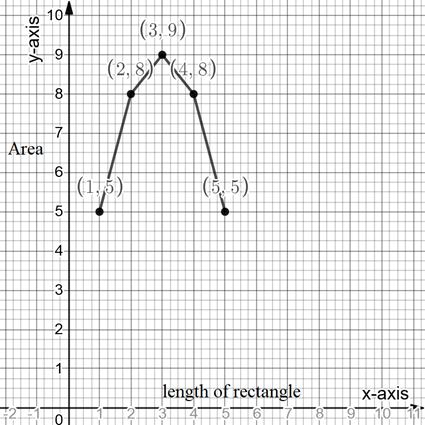
d.
To interpret: The variation of area of the rectangle with respect to the length of the rectangle
d.
Explanation of Solution
Given information: By using the result of part-c, the variation of area with the value of length is given below.
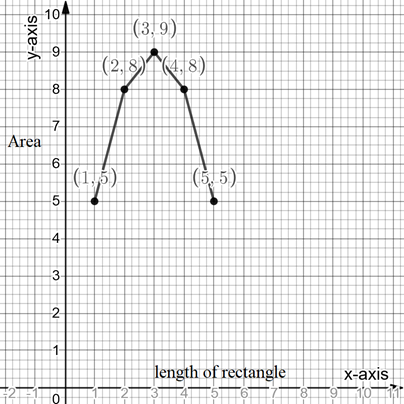
From the given information it can be observed that the area of the rectangle is continuously varying with respect to the length of the rectangle. As the length of the rectangle increases the area first increases and reaches a maximum value and then starts decreasing as the length is further increased.
The maximum value of the area of the rectangle is 9 sq. units.
The minimum value of the area of the rectangle is 5 sq. units.
e.
To find: The length and width of the rectangle for which the area of the rectangle is the greatest and the least.
e.
Answer to Problem 36PPS
The area is maximum (9) at
Explanation of Solution
Given information: By using the result of part-c, the variation of area with the value of length is given below.
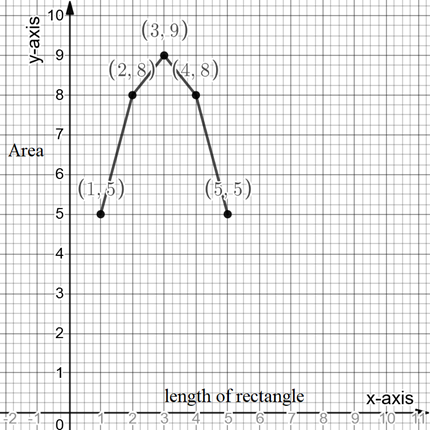
From the given information it can be observed that
The maximum value of the area is
Hence the area is maximum at
The minimum value of the area is
Hence the area is minimum at
Chapter 11 Solutions
Geometry, Student Edition
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
Introductory Statistics
College Algebra with Modeling & Visualization (5th Edition)
Elementary Statistics: Picturing the World (7th Edition)
A First Course in Probability (10th Edition)
- Can someone help me with this please?arrow_forwardMariela is in her classroom and looking out of a window at a tree, which is 20 feet away. Mariela’s line of sight to the top of the tree creates a 42° angle of elevation, and her line of sight to the base of the tree creates a 31° angle of depression. What is the height of the tree, rounded to the nearest foot? Be sure to show your work to explain how you got your answer.arrow_forward1arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

