Chapter 11.3, Problem 11WE

To determine

To Find: The area of trapezoid.

Answer to Problem 11WE

  $A=108sq.unit$

Explanation of Solution

Given:

  

  

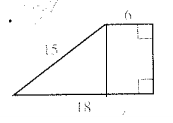
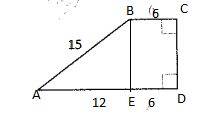
Using Pythagoras theorem in triangle $AEB$

  $\begin{array}{l}{15}^2={12}^2+B{E}^2\\ B{E}^2=225-144\\ B{E}^2=81\\ BE=9\end{array}$

Here

  $\begin{array}{l}{b}_1=6\\ b_2=18\\ h=9\end{array}$

Area of Trapezoid.

  $\begin{array}{l}A=\frac{1}{2}h(b_1+b_2)\\ A=\frac{9}{2}(6+18)\\ A=\frac{216}{2}\\ A=108sq.unit\end{array}$

Hence, area of the trapezoid is $A=108sq.unit$ .