Thinking Like an Engineer: An Active Learning Approach (4th Edition)
4th Edition
ISBN: 9780134639673
Author: Elizabeth A. Stephan, David R. Bowman, William J. Park, Benjamin L. Sill, Matthew W. Ohland
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10, Problem 16ICA
Refer to the Worksheet shown, set up to calculate the displacement of a spring. Hooke's law states that the force (F, in newtons) applied to a spring is equal to the stiffness of the spring (k, in newtons per meter) times the displacement {x, in meters): F = kx.
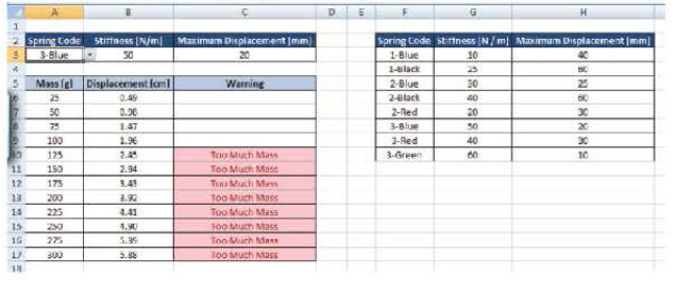
Cell A3 contains a data validation list of springs. The stiffness (cell 83) and maximum displacement (cell C3) values are found using a VLOOKUP function linked to the table shown at the right side of the worksheet. These data are then used to determine the displacement of the spring at various mass values. A warning is issued if the displacement determined is greater than the maximum displacement for the spring. Use this information to determine the answers to the following questions.
- a. Write the expression, in Excel notation, that you would type into cell 86 to determine the displacement of the spring. Assume you will copy this expression to cells 87 to B 17.
- b. Fill in the following information in the VLOOKUP function used to determine the maximum displacement in cell C3 based on the choice of spring in cell A3.
=VLOOKUP(_(1)__,_(2)_,_(3)_,_(4)_)
- c. Fill in the following information in the IF function used to determine the warning given in cell C6, using the maximum displacement in cell C3. Assume you will copy this expression to cells C7 to C17.
=IF(_(1)_,_(2)_,_(3)_)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Need help, please show all work, steps, units and please box out and round answers to 3 significant figures. Thank you!..
Need help, please show all work, steps, units and please box out and round answers to 3 significant figures. Thank you!...
FL
y
b
C
Z
Determine the moment about O due to the force F shown,
the magnitude of the force F = 76.0 lbs. Note: Pay attention
to the axis.
Values for dimensions on the figure are given in the following
table. Note the figure may not be to scale.
Variable Value
a
1.90 ft
b
2.80 ft
с
2.60 ft
d
2.30 ft
Mo
144
ft-lb
=
-212
× 1 +
xk)
☑+212
Chapter 10 Solutions
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
Ch. 10.1 - Type 5 in cell E22 and 13 in cell E23; type =E22 +...Ch. 10.1 - Type 45 into cell G22 and =G22 + 10 in cell H22....Ch. 10.1 - Type 40 into cell A28 and =A28 + 10 in cell D28....Ch. 10.1 - Type 40 into cell A28 and =A28 + 5 in cell G28....Ch. 10.2 - Launch a new worksheet. Type the following Excel...Ch. 10.2 - As part of the design of a high-performance...Ch. 10.3 - Evaluate the following expressions. What is the...Ch. 10.3 - Prob. 8CCCh. 10.4 - This is a continuation of the worksheet you...Ch. 10.5 - Prob. 11CC
Ch. 10.6 - In 1980, the Environmental Protection Agency (EPA)...Ch. 10 - A B C D E F 1 2 45 3 meters 4...Ch. 10 - A B C D E F 1 2 45 3 meters 4...Ch. 10 - A B C D E F 1 2 45 3 meters 4...Ch. 10 - A B C D E F 1 2 45 3 meters 4...Ch. 10 - ICA 10-5 The worksheet shown here was designed to...Ch. 10 - The worksheet provided was designed to calculate...Ch. 10 - Some alternate energy technologies, such as wind...Ch. 10 - The worksheet shown was designed to calculate the...Ch. 10 - The worksheet shown was designed to calculate the...Ch. 10 - Refer to the following worksheet. The following...Ch. 10 - Write the output value that would appear in a cell...Ch. 10 - Write the output value that would appear in a cell...Ch. 10 - Refer to the following worksheet. In all...Ch. 10 - Prob. 14ICACh. 10 - A bioengineer conducts clinical trials on...Ch. 10 - Refer to the Worksheet shown, set up to calculate...Ch. 10 - You are interested in analyzing different implant...Ch. 10 - You have a large stock of several values of...Ch. 10 - We accidentally drop a tomato from the balcony of...Ch. 10 - You are interested in calculating the best place...Ch. 10 - 1. A history major of your acquaintance is...Ch. 10 - Prob. 2RQCh. 10 - 3. A phase diagram for carbon and platinum is...Ch. 10 - 4. A simplified phase diagram for cobalt and...Ch. 10 - 5. You enjoy drinking coffee but are particular...Ch. 10 - 6. In the 1950s, a team at Los Alamos National...Ch. 10 - Use the following phase diagram for questions 7...Ch. 10 - Use the following phase diagram for questions 7...Ch. 10 - Use the following phase diagram for questions 9...Ch. 10 - Use the following phase diagram for questions 9...Ch. 10 - 11. When liquid and vapor coexist in a container...Ch. 10 - 12. The ideal gas law assumes that molecules...Ch. 10 - One of the NAE Grand Challenges for Engineering is...Ch. 10 - 15 Create an Excel worksheet that will allow the...Ch. 10 - Prob. 16RQ
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
?.1 Define the different reference meridians that can be used for the direction ofa line.
Elementary Surveying: An Introduction To Geomatics (15th Edition)
What is an object?
Starting Out With Visual Basic (8th Edition)
(Attributes of Hybrid Vehicles) In this chapter you learned the basics of classes. Now youll begin fleshing out...
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
In Exercises 55 through 60, find the value of the given function where a and b are numeric variables of type Do...
Introduction To Programming Using Visual Basic (11th Edition)
Describe a method that can be used to gather a piece of data such as the users age.
Web Development and Design Foundations with HTML5 (8th Edition)
Male and Female Percentages Design a program that asks the user for the number of males and the number of femal...
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 20 in. PROBLEM 15.206 Rod AB is connected by ball-and-socket joints to collar A and to the 16-in.-diameter disk C. Knowing that disk C rotates counterclockwise at the constant rate ₁ =3 rad/s in the zx plane, determine the velocity of collar A for the position shown. 25 in. B 8 in. Answer: -30 in/s =arrow_forwardB Z 001 2.5 ft PROBLEM 15.236 The arm AB of length 16 ft is used to provide an elevated platform for construction workers. In the position shown, arm AB is being raised at the constant rate de/dt = 0.25 rad/s; simultaneously, the unit is being rotated about the Y axis at the constant rate ₁ =0.15 rad/s. Knowing that 20°, determine the velocity and acceleration of Point B. Answers: 1.371 +3.76)+1.88k ft/s a=1.22 -0.342)-0.410k ft/s² Xarrow_forwardF1 3 5 4 P F2 F2 Ꮎ Ꮎ b P 3 4 5 F1 The electric pole is subject to the forces shown. Force F1 245 N and force F2 = 310 N with an angle = 20.2°. Determine the moment about point P of all forces. Take counterclockwise moments to be positive. = Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 2.50 m b 11.3 m C 13.0 m The moment about point P is 3,414 m. × N- If the moment about point P sums up to be zero. Determine the distance c while all other values remained the same. 1.26 m.arrow_forward
- Z 0.2 m B PROBLEM 15.224 Rod AB is welded to the 0.3-m-radius plate, which rotates at the constant rate ₁ = 6 rad/s. Knowing that collar D moves toward end B of the rod at a constant speed u = 1.3 m, determine, for the position shown, (a) the velocity of D, (b) the acceleration of D. Answers: 1.2 +0.5-1.2k m/s a=-7.21-14.4k m/s² A 0.25 m 0.3 marrow_forwardI am trying to code in MATLAB the equations of motion for malankovich orbitlal elements. But, I am having a problem with the B matrix. Since f matrix is 7x1 and a_d matrix has to be 3x1, the B matrix has to be 7x3. I don't know how that is possible. Can you break down the B matrix for me and let me know what size it is?arrow_forwardI am trying to code the solution to the problem in the image in MATLAB. I wanted to know what is the milankovich constraint equation that is talked about in part b.arrow_forward
- mylabmastering.pearson.com Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... P Pearson MyLab and Mastering Scoresarrow_forwardAir modeled as an ideal gas enters an insulated compressor at a temperature of 300 K and 100 kPa, and leaves at 600 kPa. The mass flowrate of air entering the compressor is 50 kg/hr, and the power consumed by the compressor is 3 kW. (Rair = 0.287 kJ/kg-K, k = 1.4, cp = 1.0045 kJ/kg-K, cv = 0.718 kJ/kg-K) Determine the isentropic exit temperature (Te,s) of the air in [K]. Determine the actual exit temperature (Te) of the air in [K]. Determine the isentropic efficiency of the compressor. (Answer: ηc,s = 93.3%) Determine the rate of entropy generated through the compressor in [kW/K]. (Answer: Ṡgen = 0.000397 kW/K)arrow_forwardmylabmastering.pearson.com Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... P Pearson MyLab and Mastering Scoresarrow_forwardA metal plate of thickness 200 mm with thermal diffusivity 5.6 x10-6 m²/s and thermal conductivity 20 W/mK is initially at a uniform temperature of 325°C. Suddenly, the 2 sides of the plate are exposed to a coolant at 15°C for which the convection heat transfer coefficient is 100 W/m²K. Determine temperatures at the surface of the plate after 3 min using (a) Lumped system analysis (b) Analytical one term approximation (c) One dimensional Semi infinite solid Analyze and discuss the resultsarrow_forwardProblem 3 This problem maps back to learning objectives 1-4 & 8. Consider the particle attached to a spring shown below. The particle has a mass m and the spring has a spring constant k. The mass-spring system makes an angle of 0 with respect to the vertical and the distance between point 0 and the particle can be defined as r. The spring is unstretched when r = l. Ꮎ g m a) How many degrees of freedom is this system and what are they? b) Derive the equation(s) of motion that govern the movement of this system.arrow_forwardChapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... Scores ■Review Determine the maximum constant speed at which the pilot can travel, so that he experiences a maximum acceleration an = 8g = 78.5 m/s². Express your answer to three significant figures and include the appropriate units. μΑ v = Value Units Submit Request Answer Part B ? Determine the normal force he exerts on the seat of the airplane when the plane is traveling at this speed and is at its lowest point. Express your answer to three significant figures and include the appropriate units. о HÅ N = Value Submit Request Answer Provide Feedback ? Units Next >arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Mechanical SPRING DESIGN Strategy and Restrictions in Under 15 Minutes!; Author: Less Boring Lectures;https://www.youtube.com/watch?v=dsWQrzfQt3s;License: Standard Youtube License