PHYSICAL CHEMISTRY-STUDENT SOLN.MAN.
2nd Edition
ISBN: 9781285074788
Author: Ball
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10, Problem 10.4E
State whether the following functions are acceptable wavefunctions over the range given. If they are not, explain why not.
(a)
(b)
(c)
(d) The function that looks like this:
(e) The function that looks like this:
Expert Solution & Answer
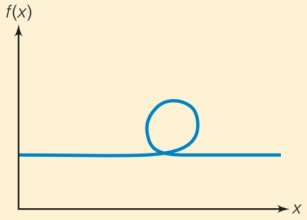
Trending nowThis is a popular solution!
Students have asked these similar questions
Imagine a particle free to move in the x direction. Which of the following
wavefunctions would be acceptable for such a particle? In each case, give your
reasons for accepting or rejecting each function.
(1) Þ(x) = x²;
(iv) y(x) = x
5.
(ii) ¥(x) = ;
(v) (x) = e-* ;
(iii) µ(x) = e-x²;
(vi) p(x) = sinx
Consider a particle of mass m confined to a one-dimensional box of length L and in a state with normalized wavefunction ψn. (a) Without evaluating any integrals, explain why ⟨x⟩ = L/2. (b) Without evaluating any integrals, explain why ⟨px⟩ = 0. (c) Derive an expression for ⟨x2⟩ (the necessary integrals will be found in the Resource section). (d) For a particle in a box the energy is given by En = n2h2/8mL2 and, because the potential energy is zero, all of this energy is kinetic. Use this observation and, without evaluating any integrals, explain why <p2x> = n2h2/4L2.
The ground-state wavefunction for a particle confined to a one dimensional box of length L is
Ψ =(2/L)½ sin (πx/L)
Suppose the box 10.0 nm long. Calculate the probability that the particle is:
(a) between x = 4.95 nm and 5.05 nm (b) between 1.95 nm and 2.05 nm, (c) between x = 9.90 and 10.00 nm, (d) in the right half of the box and (e) in the central third of the box.
Chapter 10 Solutions
PHYSICAL CHEMISTRY-STUDENT SOLN.MAN.
Ch. 10 - State the postulates of quantum mechanics...Ch. 10 - Prob. 10.2ECh. 10 - State whether the following functions are...Ch. 10 - State whether the following functions are...Ch. 10 - Prob. 10.5ECh. 10 - Prob. 10.6ECh. 10 - Evaluate the operations in parts a, b, and f in...Ch. 10 - The following operators and functions are defined:...Ch. 10 - Prob. 10.9ECh. 10 - Indicate which of these expressions yield...
Ch. 10 - Indicate which of these expressions yield an...Ch. 10 - Why is multiplying a function by a constant...Ch. 10 - Prob. 10.13ECh. 10 - Using the original definition of the momentum...Ch. 10 - Under what conditions would the operator described...Ch. 10 - A particle on a ring has a wavefunction =12eim...Ch. 10 - Calculate the uncertainty in position, x, of a...Ch. 10 - For an atom of mercury, an electron in the 1s...Ch. 10 - Classically, a hydrogen atom behaves as if it were...Ch. 10 - The largest known atom, francium, has an atomic...Ch. 10 - How is the Bohr theory of the hydrogen atom...Ch. 10 - Though not strictly equivalent, there is a similar...Ch. 10 - The uncertainty principle is related to the order...Ch. 10 - Prob. 10.24ECh. 10 - Prob. 10.25ECh. 10 - For a particle in a state having the wavefunction...Ch. 10 - Prob. 10.27ECh. 10 - A particle on a ring has a wavefunction =eim,...Ch. 10 - Prob. 10.29ECh. 10 - Prob. 10.30ECh. 10 - Prob. 10.31ECh. 10 - Normalize the following wavefunctions over the...Ch. 10 - Prob. 10.33ECh. 10 - Prob. 10.34ECh. 10 - For an unbound or free particle having mass m in...Ch. 10 - Prob. 10.36ECh. 10 - Prob. 10.37ECh. 10 - Prob. 10.38ECh. 10 - Evaluate the expression for the total energies for...Ch. 10 - Prob. 10.40ECh. 10 - Verify that the following wavefunctions are indeed...Ch. 10 - In exercise 10.41a, the wavefunction is not...Ch. 10 - Prob. 10.43ECh. 10 - Prob. 10.44ECh. 10 - Explain why n=0 is not allowed for a...Ch. 10 - Prob. 10.46ECh. 10 - Prob. 10.47ECh. 10 - Prob. 10.48ECh. 10 - Carotenes are molecules with alternating CC and...Ch. 10 - The electronic spectrum of the molecule butadiene,...Ch. 10 - Prob. 10.51ECh. 10 - Prob. 10.52ECh. 10 - Show that the normalization constants for the...Ch. 10 - Prob. 10.54ECh. 10 - Prob. 10.55ECh. 10 - An official baseball has a mass of 145g. a...Ch. 10 - Is the uncertainty principle consistent with our...Ch. 10 - Prob. 10.58ECh. 10 - Prob. 10.59ECh. 10 - Instead of x=0 to a, assume that the limits on the...Ch. 10 - In a plot of ||2, the maximum maxima in the plot...Ch. 10 - Prob. 10.62ECh. 10 - Prob. 10.63ECh. 10 - The average value of radius in a circular system,...Ch. 10 - Prob. 10.65ECh. 10 - Prob. 10.66ECh. 10 - Prob. 10.67ECh. 10 - Prob. 10.68ECh. 10 - Prob. 10.69ECh. 10 - Assume that for a particle on a ring the operator...Ch. 10 - Mathematically, the uncertainty A in some...Ch. 10 - Prob. 10.72ECh. 10 - Prob. 10.73ECh. 10 - Verify that the wavefunctions in equation 10.20...Ch. 10 - An electron is confined to a box of dimensions...Ch. 10 - a What is the ratio of energy levels having the...Ch. 10 - Consider a one-dimensional particle-in-a-box and a...Ch. 10 - Prob. 10.78ECh. 10 - Prob. 10.79ECh. 10 - Prob. 10.80ECh. 10 - Prob. 10.81ECh. 10 - What are x,y, and z for 111 of a 3-D...Ch. 10 - Prob. 10.83ECh. 10 - Prob. 10.84ECh. 10 - Prob. 10.85ECh. 10 - Prob. 10.86ECh. 10 - Prob. 10.87ECh. 10 - Prob. 10.88ECh. 10 - Substitute (x,t)=eiEt/(x) into the time-dependent...Ch. 10 - Write (x,t)=eiEt/(x) in terms of sine and cosine,...Ch. 10 - Prob. 10.91ECh. 10 - Prob. 10.92ECh. 10 - Prob. 10.93ECh. 10 - Prob. 10.95E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Similar questions
- What is the physical explanation of the difference between a particle having the 3-D rotational wavefunction 3,2 and an identical particle having the wavefunction 3,2?arrow_forwardFor a particle in a state having the wavefunction =2asinxa in the range x=0toa, what is the probability that the particle exists in the following intervals? a x=0to0.02ab x=0.24ato0.26a c x=0.49ato0.51ad x=0.74ato0.76a e x=0.98ato1.00a Plot the probabilities versus x. What does your plot illustrate about the probability?arrow_forwardBased on the trend shown in Figure 11.5, draw the probability distribution of a harmonic oscillator wavefunction that has a very high value of n. Explain how this is consistent with the correspondence principle.arrow_forward
- [p* L₂ da 0 HO H + →arrow_forwardwavefunction iš E7D.5(b) Calculate the probability that a particle will be found between 0.65L and 0.671 in a box of length L for the case where the wavefunction is (i) Y, (ii) y.. You may make the same approximation as in Exercise E7D.5(a).arrow_forwardConsider a fictitious one-dimensional system with one electron.The wave function for the electron, drawn below, isψ (x)= sin x from x = 0 to x = 2π. (a) Sketch the probabilitydensity, ψ2(x), from x = 0 to x = 2π. (b) At what value orvalues of x will there be the greatest probability of finding theelectron? (c) What is the probability that the electron willbe found at x = π? What is such a point in a wave functioncalled?arrow_forward
- Imagine a particle free to move in the x direction. Which of the following wavefunctions would be acceptable for such a particle? In eachcase, give your reasons for accepting or rejecting each function. (i) Ψ(x)=x2; (ii) Ψ(x)=1/x; (iii) Ψ(x)=e-x^2.arrow_forwardIf two wavefunctions, Wa and Wb, are orthonormal and degenerate, then what is true about the linear combinations 1 1 w. +v.) a a and (a) y+ and y- are orthonormal. (b) y+ and y- are no longer eigenfunctions of the Schrödinger equation. (c) V+ and y- have the same energy. (d) V+ and Y- have the same probability density distribution.arrow_forwardConsider the three spherical harmonics (a) Y0,0, (b) Y2,–1, and (c) Y3,+3. (a) For each spherical harmonic, substitute the explicit form of the function taken from Table 7F.1 into the left-hand side of eqn 7F.8 (the Schrödinger equation for a particle on a sphere) and confirm that the function is a solution of the equation; give the corresponding eigenvalue (the energy) and show that it agrees with eqn 7F.10. (b) Likewise, show that each spherical harmonic is an eigenfunction of lˆz = (ℏ/i)(d/dϕ) and give the eigenvalue in each case.arrow_forward
- Write the normalized form of the ground state wavefunction of the harmonic oscillator in terms of the variable y and the parameter α. (a) Write the integral you would need to evaluate to find the mean displacement <y>, and then use a symmetry argument to explain why this integral is equal to 0. (b) Calculate <y2> (the necessary integral will be found in the Resource section). (c) Repeat the process for the first excited state.arrow_forwardE7D.5(b) Calculate the probability that a particle will be found between 0.65L and 0.67L in a box of length L for the case where the wavefunction is (i) ₁, (ii) V₂. You may make the same approximation as in Exercise E7D.5(a). pr E7 po prarrow_forwardCalculate the probability that a particle will be found between 0.49L and 0.51L in a box of length L for (i) ψ1, (ii) ψ2. You may assume that the wavefunction is constant in this range, so the probability is ψ2δx.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Physical Chemistry
Chemistry
ISBN:9781133958437
Author:Ball, David W. (david Warren), BAER, Tomas
Publisher:Wadsworth Cengage Learning,
Introductory Chemistry: A Foundation
Chemistry
ISBN:9781337399425
Author:Steven S. Zumdahl, Donald J. DeCoste
Publisher:Cengage Learning
Quantum Mechanics - Part 1: Crash Course Physics #43; Author: CrashCourse;https://www.youtube.com/watch?v=7kb1VT0J3DE;License: Standard YouTube License, CC-BY