
McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Question
Chapter 9.6, Problem 20WE
To determine
The value of
Expert Solution & Answer
Answer to Problem 20WE
The value of
Explanation of Solution
Given information:
It is given
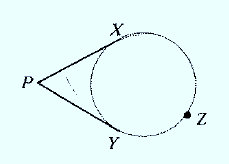
Given
Therefore,
The measure of an
Therefore from given figure
Therefore, the value of
Chapter 9 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 9.1 - Prob. 1CECh. 9.1 - Prob. 2CECh. 9.1 - Prob. 3CECh. 9.1 - Prob. 4CECh. 9.1 - Prob. 5CECh. 9.1 - Prob. 6CECh. 9.1 - Prob. 7CECh. 9.1 - Prob. 8CECh. 9.1 - Prob. 9CECh. 9.1 - Prob. 10CE
Ch. 9.1 - Prob. 11CECh. 9.1 - Prob. 1WECh. 9.1 - Prob. 2WECh. 9.1 - Prob. 3WECh. 9.1 - Prob. 4WECh. 9.1 - Prob. 5WECh. 9.1 - Prob. 6WECh. 9.1 - Prob. 7WECh. 9.1 - Prob. 8WECh. 9.1 - Prob. 9WECh. 9.1 - Prob. 10WECh. 9.1 - Prob. 11WECh. 9.1 - Prob. 12WECh. 9.1 - Prob. 13WECh. 9.1 - Prob. 14WECh. 9.1 - Prob. 15WECh. 9.1 - Prob. 16WECh. 9.1 - Prob. 17WECh. 9.1 - Prob. 18WECh. 9.1 - Prob. 19WECh. 9.1 - Prob. 20WECh. 9.1 - Prob. 1ECh. 9.1 - Prob. 2ECh. 9.1 - Prob. 3ECh. 9.1 - Prob. 4ECh. 9.1 - Prob. 5ECh. 9.2 - Prob. 1CECh. 9.2 - Prob. 2CECh. 9.2 - Prob. 3CECh. 9.2 - Prob. 4CECh. 9.2 - Prob. 5CECh. 9.2 - Prob. 1WECh. 9.2 - Prob. 2WECh. 9.2 - Prob. 3WECh. 9.2 - Prob. 4WECh. 9.2 - Prob. 5WECh. 9.2 - Prob. 6WECh. 9.2 - Prob. 7WECh. 9.2 - Prob. 8WECh. 9.2 - Prob. 9WECh. 9.2 - Prob. 10WECh. 9.2 - Prob. 11WECh. 9.2 - Prob. 12WECh. 9.2 - Prob. 13WECh. 9.2 - Prob. 14WECh. 9.2 - Prob. 15WECh. 9.2 - Prob. 16WECh. 9.2 - Prob. 17WECh. 9.2 - Prob. 18WECh. 9.2 - Prob. 19WECh. 9.2 - Prob. 20WECh. 9.2 - Prob. 21WECh. 9.2 - Prob. 22WECh. 9.2 - Prob. 23WECh. 9.2 - Prob. 1MRECh. 9.2 - Prob. 2MRECh. 9.2 - Prob. 3MRECh. 9.3 - Prob. 1CECh. 9.3 - Prob. 2CECh. 9.3 - Prob. 3CECh. 9.3 - Prob. 4CECh. 9.3 - Prob. 5CECh. 9.3 - Prob. 6CECh. 9.3 - Prob. 7CECh. 9.3 - Prob. 8CECh. 9.3 - Prob. 9CECh. 9.3 - Prob. 10CECh. 9.3 - Prob. 11CECh. 9.3 - Prob. 12CECh. 9.3 - Prob. 13CECh. 9.3 - Prob. 1WECh. 9.3 - Prob. 2WECh. 9.3 - Prob. 3WECh. 9.3 - Prob. 4WECh. 9.3 - Prob. 5WECh. 9.3 - Prob. 6WECh. 9.3 - Prob. 7WECh. 9.3 - Prob. 8WECh. 9.3 - Prob. 9WECh. 9.3 - Prob. 10WECh. 9.3 - Prob. 11WECh. 9.3 - Prob. 12WECh. 9.3 - Prob. 13WECh. 9.3 - Prob. 14WECh. 9.3 - Prob. 15WECh. 9.3 - Prob. 16WECh. 9.3 - Prob. 17WECh. 9.3 - Prob. 18WECh. 9.3 - Prob. 19WECh. 9.3 - Prob. 20WECh. 9.3 - Prob. 21WECh. 9.3 - Prob. 22WECh. 9.3 - Prob. 23WECh. 9.3 - Prob. 24WECh. 9.4 - Prob. 1CECh. 9.4 - Prob. 2CECh. 9.4 - Prob. 3CECh. 9.4 - Prob. 4CECh. 9.4 - Prob. 5CECh. 9.4 - Prob. 6CECh. 9.4 - Prob. 7CECh. 9.4 - Prob. 1WECh. 9.4 - Prob. 2WECh. 9.4 - Prob. 3WECh. 9.4 - Prob. 4WECh. 9.4 - Prob. 5WECh. 9.4 - Prob. 6WECh. 9.4 - Prob. 7WECh. 9.4 - Prob. 8WECh. 9.4 - Prob. 9WECh. 9.4 - Prob. 10WECh. 9.4 - Prob. 11WECh. 9.4 - Prob. 12WECh. 9.4 - Prob. 13WECh. 9.4 - Prob. 14WECh. 9.4 - Prob. 15WECh. 9.4 - Prob. 16WECh. 9.4 - Prob. 17WECh. 9.4 - Prob. 18WECh. 9.4 - Prob. 19WECh. 9.4 - Prob. 20WECh. 9.4 - Prob. 21WECh. 9.4 - Prob. 22WECh. 9.4 - Prob. 23WECh. 9.4 - Prob. 24WECh. 9.4 - Prob. 25WECh. 9.4 - Prob. 26WECh. 9.4 - Prob. 27WECh. 9.4 - Prob. 1ST1Ch. 9.4 - Prob. 2ST1Ch. 9.4 - Prob. 3ST1Ch. 9.4 - Prob. 4ST1Ch. 9.4 - Prob. 5ST1Ch. 9.4 - Prob. 6ST1Ch. 9.5 - Prob. 1CECh. 9.5 - Prob. 2CECh. 9.5 - Prob. 3CECh. 9.5 - Prob. 4CECh. 9.5 - Prob. 5CECh. 9.5 - Prob. 6CECh. 9.5 - Prob. 7CECh. 9.5 - Prob. 8CECh. 9.5 - Prob. 9CECh. 9.5 - Prob. 10CECh. 9.5 - Prob. 11CECh. 9.5 - Prob. 12CECh. 9.5 - Prob. 13CECh. 9.5 - Prob. 14CECh. 9.5 - Prob. 1WECh. 9.5 - Prob. 2WECh. 9.5 - Prob. 3WECh. 9.5 - Prob. 4WECh. 9.5 - Prob. 5WECh. 9.5 - Prob. 6WECh. 9.5 - Prob. 7WECh. 9.5 - Prob. 8WECh. 9.5 - Prob. 9WECh. 9.5 - Prob. 10WECh. 9.5 - Prob. 11WECh. 9.5 - Prob. 12WECh. 9.5 - Prob. 13WECh. 9.5 - Prob. 14WECh. 9.5 - Prob. 15WECh. 9.5 - Prob. 16WECh. 9.5 - Prob. 17WECh. 9.5 - Prob. 18WECh. 9.5 - Prob. 19WECh. 9.5 - Prob. 20WECh. 9.5 - Prob. 21WECh. 9.5 - Prob. 22WECh. 9.5 - Prob. 23WECh. 9.5 - Prob. 24WECh. 9.5 - Prob. 25WECh. 9.5 - Prob. 26WECh. 9.5 - Prob. 27WECh. 9.5 - Prob. 28WECh. 9.5 - Prob. 29WECh. 9.5 - Prob. 1MRECh. 9.5 - Prob. 2MRECh. 9.5 - Prob. 3MRECh. 9.5 - Prob. 4MRECh. 9.5 - Prob. 5MRECh. 9.5 - Prob. 6MRECh. 9.6 - Prob. 1CECh. 9.6 - Prob. 2CECh. 9.6 - Prob. 3CECh. 9.6 - Prob. 4CECh. 9.6 - Prob. 5CECh. 9.6 - Prob. 6CECh. 9.6 - Prob. 7CECh. 9.6 - Prob. 8CECh. 9.6 - Prob. 9CECh. 9.6 - Prob. 10CECh. 9.6 - Prob. 1WECh. 9.6 - Prob. 2WECh. 9.6 - Prob. 3WECh. 9.6 - Prob. 4WECh. 9.6 - Prob. 5WECh. 9.6 - Prob. 6WECh. 9.6 - Prob. 7WECh. 9.6 - Prob. 8WECh. 9.6 - Prob. 9WECh. 9.6 - Prob. 10WECh. 9.6 - Prob. 11WECh. 9.6 - Prob. 12WECh. 9.6 - Prob. 13WECh. 9.6 - Prob. 14WECh. 9.6 - Prob. 15WECh. 9.6 - Prob. 16WECh. 9.6 - Prob. 17WECh. 9.6 - Prob. 18WECh. 9.6 - Prob. 19WECh. 9.6 - Prob. 20WECh. 9.6 - Prob. 21WECh. 9.6 - Prob. 22WECh. 9.6 - Prob. 23WECh. 9.6 - Prob. 24WECh. 9.6 - Prob. 25WECh. 9.6 - Prob. 26WECh. 9.6 - Prob. 27WECh. 9.6 - Prob. 28WECh. 9.6 - Prob. 29WECh. 9.6 - Prob. 30WECh. 9.6 - Prob. 31WECh. 9.6 - Prob. 32WECh. 9.6 - Prob. 1EXCh. 9.6 - Prob. 2EXCh. 9.6 - Prob. 3EXCh. 9.7 - Prob. 1CECh. 9.7 - Prob. 2CECh. 9.7 - Prob. 3CECh. 9.7 - Prob. 4CECh. 9.7 - Prob. 5CECh. 9.7 - Prob. 6CECh. 9.7 - Prob. 7CECh. 9.7 - Prob. 1WECh. 9.7 - Prob. 2WECh. 9.7 - Prob. 3WECh. 9.7 - Prob. 4WECh. 9.7 - Prob. 5WECh. 9.7 - Prob. 6WECh. 9.7 - Prob. 7WECh. 9.7 - Prob. 8WECh. 9.7 - Prob. 9WECh. 9.7 - Prob. 10WECh. 9.7 - Prob. 11WECh. 9.7 - Prob. 12WECh. 9.7 - Prob. 13WECh. 9.7 - Prob. 14WECh. 9.7 - Prob. 15WECh. 9.7 - Prob. 16WECh. 9.7 - Prob. 17WECh. 9.7 - Prob. 18WECh. 9.7 - Prob. 19WECh. 9.7 - Prob. 20WECh. 9.7 - Prob. 21WECh. 9.7 - Prob. 22WECh. 9.7 - Prob. 23WECh. 9.7 - Prob. 24WECh. 9.7 - Prob. 25WECh. 9.7 - Prob. 26WECh. 9.7 - Prob. 27WECh. 9.7 - Prob. 28WECh. 9.7 - Prob. 1ST2Ch. 9.7 - Prob. 2ST2Ch. 9.7 - Prob. 3ST2Ch. 9.7 - Prob. 4ST2Ch. 9.7 - Prob. 5ST2Ch. 9.7 - Prob. 6ST2Ch. 9.7 - Prob. 7ST2Ch. 9.7 - Prob. 8ST2Ch. 9.7 - Prob. 1ECh. 9.7 - Prob. 2ECh. 9.7 - Prob. 3ECh. 9.7 - Prob. 4ECh. 9.7 - Prob. 5ECh. 9 - Prob. 1CRCh. 9 - Prob. 2CRCh. 9 - Prob. 3CRCh. 9 - Prob. 4CRCh. 9 - Prob. 5CRCh. 9 - Prob. 6CRCh. 9 - Prob. 7CRCh. 9 - Prob. 8CRCh. 9 - Prob. 9CRCh. 9 - Prob. 10CRCh. 9 - Prob. 11CRCh. 9 - Prob. 12CRCh. 9 - Prob. 13CRCh. 9 - Prob. 14CRCh. 9 - Prob. 15CRCh. 9 - Prob. 16CRCh. 9 - Prob. 17CRCh. 9 - Prob. 18CRCh. 9 - Prob. 19CRCh. 9 - Prob. 20CRCh. 9 - Prob. 21CRCh. 9 - Prob. 22CRCh. 9 - Prob. 23CRCh. 9 - Prob. 24CRCh. 9 - Prob. 1CTCh. 9 - Prob. 2CTCh. 9 - Prob. 3CTCh. 9 - Prob. 4CTCh. 9 - Prob. 5CTCh. 9 - Prob. 6CTCh. 9 - Prob. 7CTCh. 9 - Prob. 8CTCh. 9 - Prob. 9CTCh. 9 - Prob. 10CTCh. 9 - Prob. 11CTCh. 9 - Prob. 12CTCh. 9 - Prob. 13CTCh. 9 - Prob. 14CTCh. 9 - Prob. 15CTCh. 9 - Prob. 16CTCh. 9 - Prob. 17CTCh. 9 - Prob. 18CTCh. 9 - Prob. 1CURCh. 9 - Prob. 2CURCh. 9 - Prob. 3CURCh. 9 - Prob. 4CURCh. 9 - Prob. 5CURCh. 9 - Prob. 6CURCh. 9 - Prob. 7CURCh. 9 - Prob. 8CURCh. 9 - Prob. 9CURCh. 9 - Prob. 10CURCh. 9 - Prob. 11CURCh. 9 - Prob. 12CURCh. 9 - Prob. 13CURCh. 9 - Prob. 14CURCh. 9 - Prob. 15CURCh. 9 - Prob. 16CURCh. 9 - Prob. 17CURCh. 9 - Prob. 18CURCh. 9 - Prob. 19CURCh. 9 - Prob. 20CURCh. 9 - Prob. 21CURCh. 9 - Prob. 22CURCh. 9 - Prob. 23CURCh. 9 - Prob. 24CURCh. 9 - Prob. 25CURCh. 9 - Prob. 26CURCh. 9 - Prob. 27CURCh. 9 - Prob. 28CURCh. 9 - Prob. 29CURCh. 9 - Prob. 30CUR
Additional Math Textbook Solutions
Find more solutions based on key concepts
The given sentence “A null or empty set is the symbol (ϕ,λ) ” with the correct term.
Pre-Algebra Student Edition
CHECK POINT 1 Find a counterexample to show that the statement The product of two two-digit numbers is a three-...
Thinking Mathematically (6th Edition)
Using the definition, calculate the derivatives of the functions in Exercises 1–6. Then find the values of the ...
University Calculus: Early Transcendentals (4th Edition)
Draining a tank An inverted conical water tank with a height of 12 ft and a radius of 6 ft is drained through a...
Calculus: Early Transcendentals (2nd Edition)
4. Correlation and Causation What is meant by the statement that “correlation does imply causation”?
Elementary Statistics
Read about basic ideas of statistics in Common Core Standards for grades 3-5, and discuss why students at these...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Can you cut the 12 glass triangles from a sheet of glass that is 4 feet by 8 feet? If so, how can it be done?arrow_forwardCan you cut 12 glass triangles from a sheet of glass that is 4 feet by 8 feet? If so, draw a diagram of how it can be done.arrow_forwardIn triangle with sides of lengths a, b and c the angle a lays opposite to a. Prove the following inequality sin a 2√bc C α b a Warrow_forward
- Find the values of x, y, and z. Round to the nearest tenth, if necessary. 8, 23arrow_forward11 In the Pharlemina's Favorite quilt pattern below, vega-pxe-frame describe a motion that will take part (a) green to part (b) blue. Part (a) Part (b)arrow_forward5. 156 m/WXY = 59° 63 E 7. B E 101 C mFE = 6. 68° 8. C 17arrow_forward
- 1/6/25, 3:55 PM Question: 14 Similar right triangles EFG and HIJ are shown. re of 120 √65 adjacent E hypotenuse adjaca H hypotenuse Item Bank | DnA Er:nollesup .es/prist Sisupe ed 12um jerit out i al F 4 G I oppe J 18009 90 ODPO ysma brs & eaus ps sd jon yem What is the value of tan J? ed on yem O broppo 4 ○ A. √65 Qx oppoEF Adj art saused taupe ed for yem 4 ○ B. √65 29 asipnisht riod 916 zelprisht rad √65 4 O ○ C. 4 √65 O D. VIS 9 OD elimiz 916 aelonsider saused supsarrow_forwardFind all anglesarrow_forwardFind U V . 10 U V T 64° Write your answer as an integer or as a decimal rounded to the nearest tenth. U V = Entregararrow_forward
- Find the area of a square whose diagonal is 10arrow_forwardDecomposition geometry: Mary is making a decorative yard space with dimensions as shaded in green (ΔOAB).Mary would like to cover the yard space with artificial turf (plastic grass-like rug). Mary reasoned that she could draw a rectangle around the figure so that the point O was at a vertex of the rectangle and that points A and B were on sides of the rectangle. Then she reasoned that the three smaller triangles resulting could be subtracted from the area of the rectangle. Mary determined that she would need 28 square meters of artificial turf to cover the green shaded yard space pictured exactly.arrow_forward7. 11 m 12.7 m 14 m S V=B₁+ B2(h) 9.5 m 16 m h+s 2 na 62-19 = 37 +, M h² = Bu-29arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Implicit Differentiation Explained - Product Rule, Quotient & Chain Rule - Calculus; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=LGY-DjFsALc;License: Standard YouTube License, CC-BY