Chapter 9.1, Problem 20WE

a)

To determine

To find:Perpendicular bisectors of two chords $\overline{AB}$ and $\overline{BC}$ as shown in given circle. Also to find point of intersection of these two bisectors.

Explanation of Solution

Required perpendicular bisectors are shown in below figure, so they both intersect at the center of the circle at O.

  

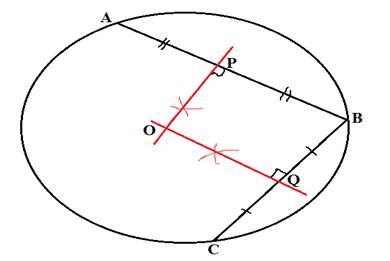
Giveninformation: A circle in which two chords $\overline{AB}$ and $\overline{BC}$ are given.

Procedure:To draw perpendicular bisector of a line, mark two arcs from its two end points on both sides of line, filling more than half distance of this line. And then join these intersecting points, so that the resulting line is the required perpendicular bisector of given line.

Calculation:Using the same concept, draw the perpendicular bisectors of chords $\overline{AB}$ and $\overline{BC}$ so that both intersect each other at point O that is actually the center of the circle. It is because of the property of circle that any perpendicular bisector to a chord, always passes from the center of the circle.

Conclusion:So, the intersecting point of these two perpendicular bisectors appear to be at the center of the circle.

b)

To determine

To find:An argument that justify the answer of part (a).

Answer to Problem 20WE

Argument is the property of circle that,” Any perpendicular from center of a circle to its chord, always bisects the chord.”

Explanation of Solution

Giveninformation: A circle in which two chords $\overline{AB}$ and $\overline{BC}$ are given.

Concept used:In a circle, any perpendicular drawn from its center to a chord always bisects the chord. The same concept is used in drawing perpendicular bisectors of given chord , so that their intersecting point is the center of the circle.

Calculation:Once drawing is done, it measures the distance of intersecting point to the perpendicular bisectors from the end points of the chord are equal, i.e.,

  $OA=OB=OC$

So that these three are the radii of this circle and hence point O is the center of the circle by the definition of circle.

Conclusion:So,the above argument justifies that this intersecting point O is surely the center of the circle given.