Chapter 9.1, Problem 5E

To determine

To describe: Koenigsberg bridge problem.

Answer to Problem 5E

It is impossible to walk along 7 bridges in a Koenigsberg problem because there are more than 2 odd vertices which cannot be traced without backtracking.

Explanation of Solution

Given:

Koenigsberg bridge problem

Calculation:

A point is called a vertex.

A line is called an edge.

The number edges that lead to a vertex is called the degree of the vertex.

A route around a graph that visits every vertex once is called a simple path.

A route around a graph that visits every edge once is called an Euler path.

In an Euler path, the number of vertices of odd degree must be either zero or two.

For the Koenigsberg problem, consider the simplified figure of the bridge in the form of a graph:

  

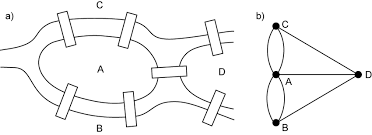
Vertices B, C and D have degree 3 and vertex A has degree 5, so this graph has four vertices of odd degree. So, it does not have an Euler path.

Conclusion:

Therefore, the Koenigsberg problem is impossible to solve without backtracking.