McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Question
Chapter 9.2, Problem 21WE
a)
To determine
To find: the number of planes that can be drawn tangent to each of the spheres.
a)
Expert Solution
Answer to Problem 21WE
There are infinite numbers of planes that are tangent to each of the spheres.
Explanation of Solution
Given Information:
Given figure,
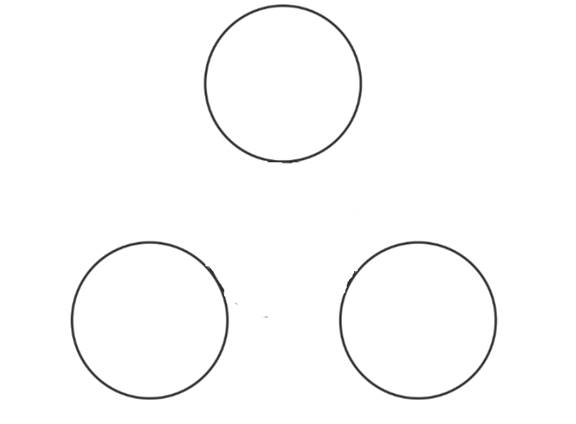
Calculation:
Consider three spheres as shown in the figure below.
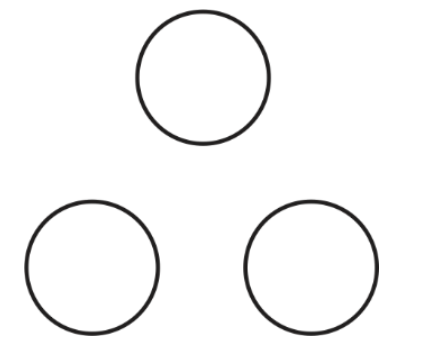
It is required to find the number of planes that can be drawn tangent to each of the spheres.
A sphere is a locus of points in a space which are equidistant from a fixed point.
There are infinite numbers of points on the surface of a sphere.
Through each of these points, a plane can be drawn tangent to the surface of a sphere.
Therefore, there are infinite numbers of planes that are tangent to each of the spheres.
b)
To determine
To find: the number of spheres that can be drawn tangent to all three spheres.
b)
Expert Solution
Answer to Problem 21WE
There can be only one such sphere which lies at the center of three spheres.
Explanation of Solution
Given Information:
Given figure,
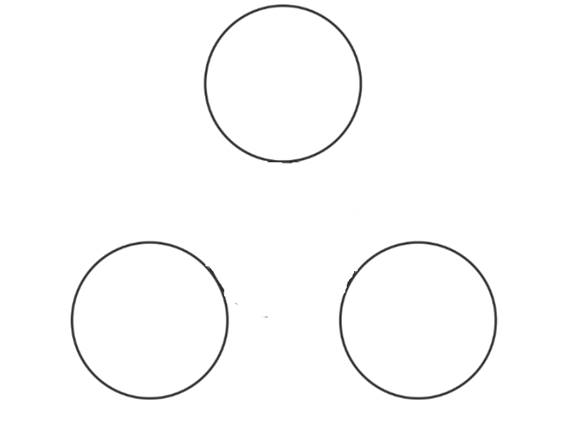
Calculation:
It is required to find the number of spheres which are tangent to each of the spheres.
The above figure shows three spheres, two in a row and then one directly above this row.
The three spheres seem congruent to each other.
It is required to draw spheres which are tangent to all the three given spheres.
There can be only one such sphere which lies at the center of three spheres.
The figure is shown below:
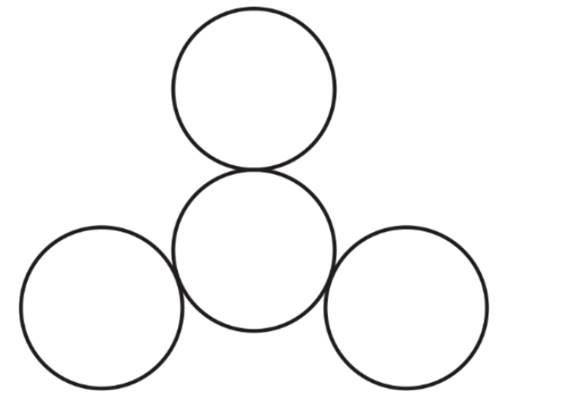
Chapter 9 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 9.1 - Prob. 1CECh. 9.1 - Prob. 2CECh. 9.1 - Prob. 3CECh. 9.1 - Prob. 4CECh. 9.1 - Prob. 5CECh. 9.1 - Prob. 6CECh. 9.1 - Prob. 7CECh. 9.1 - Prob. 8CECh. 9.1 - Prob. 9CECh. 9.1 - Prob. 10CE
Ch. 9.1 - Prob. 11CECh. 9.1 - Prob. 1WECh. 9.1 - Prob. 2WECh. 9.1 - Prob. 3WECh. 9.1 - Prob. 4WECh. 9.1 - Prob. 5WECh. 9.1 - Prob. 6WECh. 9.1 - Prob. 7WECh. 9.1 - Prob. 8WECh. 9.1 - Prob. 9WECh. 9.1 - Prob. 10WECh. 9.1 - Prob. 11WECh. 9.1 - Prob. 12WECh. 9.1 - Prob. 13WECh. 9.1 - Prob. 14WECh. 9.1 - Prob. 15WECh. 9.1 - Prob. 16WECh. 9.1 - Prob. 17WECh. 9.1 - Prob. 18WECh. 9.1 - Prob. 19WECh. 9.1 - Prob. 20WECh. 9.1 - Prob. 1ECh. 9.1 - Prob. 2ECh. 9.1 - Prob. 3ECh. 9.1 - Prob. 4ECh. 9.1 - Prob. 5ECh. 9.2 - Prob. 1CECh. 9.2 - Prob. 2CECh. 9.2 - Prob. 3CECh. 9.2 - Prob. 4CECh. 9.2 - Prob. 5CECh. 9.2 - Prob. 1WECh. 9.2 - Prob. 2WECh. 9.2 - Prob. 3WECh. 9.2 - Prob. 4WECh. 9.2 - Prob. 5WECh. 9.2 - Prob. 6WECh. 9.2 - Prob. 7WECh. 9.2 - Prob. 8WECh. 9.2 - Prob. 9WECh. 9.2 - Prob. 10WECh. 9.2 - Prob. 11WECh. 9.2 - Prob. 12WECh. 9.2 - Prob. 13WECh. 9.2 - Prob. 14WECh. 9.2 - Prob. 15WECh. 9.2 - Prob. 16WECh. 9.2 - Prob. 17WECh. 9.2 - Prob. 18WECh. 9.2 - Prob. 19WECh. 9.2 - Prob. 20WECh. 9.2 - Prob. 21WECh. 9.2 - Prob. 22WECh. 9.2 - Prob. 23WECh. 9.2 - Prob. 1MRECh. 9.2 - Prob. 2MRECh. 9.2 - Prob. 3MRECh. 9.3 - Prob. 1CECh. 9.3 - Prob. 2CECh. 9.3 - Prob. 3CECh. 9.3 - Prob. 4CECh. 9.3 - Prob. 5CECh. 9.3 - Prob. 6CECh. 9.3 - Prob. 7CECh. 9.3 - Prob. 8CECh. 9.3 - Prob. 9CECh. 9.3 - Prob. 10CECh. 9.3 - Prob. 11CECh. 9.3 - Prob. 12CECh. 9.3 - Prob. 13CECh. 9.3 - Prob. 1WECh. 9.3 - Prob. 2WECh. 9.3 - Prob. 3WECh. 9.3 - Prob. 4WECh. 9.3 - Prob. 5WECh. 9.3 - Prob. 6WECh. 9.3 - Prob. 7WECh. 9.3 - Prob. 8WECh. 9.3 - Prob. 9WECh. 9.3 - Prob. 10WECh. 9.3 - Prob. 11WECh. 9.3 - Prob. 12WECh. 9.3 - Prob. 13WECh. 9.3 - Prob. 14WECh. 9.3 - Prob. 15WECh. 9.3 - Prob. 16WECh. 9.3 - Prob. 17WECh. 9.3 - Prob. 18WECh. 9.3 - Prob. 19WECh. 9.3 - Prob. 20WECh. 9.3 - Prob. 21WECh. 9.3 - Prob. 22WECh. 9.3 - Prob. 23WECh. 9.3 - Prob. 24WECh. 9.4 - Prob. 1CECh. 9.4 - Prob. 2CECh. 9.4 - Prob. 3CECh. 9.4 - Prob. 4CECh. 9.4 - Prob. 5CECh. 9.4 - Prob. 6CECh. 9.4 - Prob. 7CECh. 9.4 - Prob. 1WECh. 9.4 - Prob. 2WECh. 9.4 - Prob. 3WECh. 9.4 - Prob. 4WECh. 9.4 - Prob. 5WECh. 9.4 - Prob. 6WECh. 9.4 - Prob. 7WECh. 9.4 - Prob. 8WECh. 9.4 - Prob. 9WECh. 9.4 - Prob. 10WECh. 9.4 - Prob. 11WECh. 9.4 - Prob. 12WECh. 9.4 - Prob. 13WECh. 9.4 - Prob. 14WECh. 9.4 - Prob. 15WECh. 9.4 - Prob. 16WECh. 9.4 - Prob. 17WECh. 9.4 - Prob. 18WECh. 9.4 - Prob. 19WECh. 9.4 - Prob. 20WECh. 9.4 - Prob. 21WECh. 9.4 - Prob. 22WECh. 9.4 - Prob. 23WECh. 9.4 - Prob. 24WECh. 9.4 - Prob. 25WECh. 9.4 - Prob. 26WECh. 9.4 - Prob. 27WECh. 9.4 - Prob. 1ST1Ch. 9.4 - Prob. 2ST1Ch. 9.4 - Prob. 3ST1Ch. 9.4 - Prob. 4ST1Ch. 9.4 - Prob. 5ST1Ch. 9.4 - Prob. 6ST1Ch. 9.5 - Prob. 1CECh. 9.5 - Prob. 2CECh. 9.5 - Prob. 3CECh. 9.5 - Prob. 4CECh. 9.5 - Prob. 5CECh. 9.5 - Prob. 6CECh. 9.5 - Prob. 7CECh. 9.5 - Prob. 8CECh. 9.5 - Prob. 9CECh. 9.5 - Prob. 10CECh. 9.5 - Prob. 11CECh. 9.5 - Prob. 12CECh. 9.5 - Prob. 13CECh. 9.5 - Prob. 14CECh. 9.5 - Prob. 1WECh. 9.5 - Prob. 2WECh. 9.5 - Prob. 3WECh. 9.5 - Prob. 4WECh. 9.5 - Prob. 5WECh. 9.5 - Prob. 6WECh. 9.5 - Prob. 7WECh. 9.5 - Prob. 8WECh. 9.5 - Prob. 9WECh. 9.5 - Prob. 10WECh. 9.5 - Prob. 11WECh. 9.5 - Prob. 12WECh. 9.5 - Prob. 13WECh. 9.5 - Prob. 14WECh. 9.5 - Prob. 15WECh. 9.5 - Prob. 16WECh. 9.5 - Prob. 17WECh. 9.5 - Prob. 18WECh. 9.5 - Prob. 19WECh. 9.5 - Prob. 20WECh. 9.5 - Prob. 21WECh. 9.5 - Prob. 22WECh. 9.5 - Prob. 23WECh. 9.5 - Prob. 24WECh. 9.5 - Prob. 25WECh. 9.5 - Prob. 26WECh. 9.5 - Prob. 27WECh. 9.5 - Prob. 28WECh. 9.5 - Prob. 29WECh. 9.5 - Prob. 1MRECh. 9.5 - Prob. 2MRECh. 9.5 - Prob. 3MRECh. 9.5 - Prob. 4MRECh. 9.5 - Prob. 5MRECh. 9.5 - Prob. 6MRECh. 9.6 - Prob. 1CECh. 9.6 - Prob. 2CECh. 9.6 - Prob. 3CECh. 9.6 - Prob. 4CECh. 9.6 - Prob. 5CECh. 9.6 - Prob. 6CECh. 9.6 - Prob. 7CECh. 9.6 - Prob. 8CECh. 9.6 - Prob. 9CECh. 9.6 - Prob. 10CECh. 9.6 - Prob. 1WECh. 9.6 - Prob. 2WECh. 9.6 - Prob. 3WECh. 9.6 - Prob. 4WECh. 9.6 - Prob. 5WECh. 9.6 - Prob. 6WECh. 9.6 - Prob. 7WECh. 9.6 - Prob. 8WECh. 9.6 - Prob. 9WECh. 9.6 - Prob. 10WECh. 9.6 - Prob. 11WECh. 9.6 - Prob. 12WECh. 9.6 - Prob. 13WECh. 9.6 - Prob. 14WECh. 9.6 - Prob. 15WECh. 9.6 - Prob. 16WECh. 9.6 - Prob. 17WECh. 9.6 - Prob. 18WECh. 9.6 - Prob. 19WECh. 9.6 - Prob. 20WECh. 9.6 - Prob. 21WECh. 9.6 - Prob. 22WECh. 9.6 - Prob. 23WECh. 9.6 - Prob. 24WECh. 9.6 - Prob. 25WECh. 9.6 - Prob. 26WECh. 9.6 - Prob. 27WECh. 9.6 - Prob. 28WECh. 9.6 - Prob. 29WECh. 9.6 - Prob. 30WECh. 9.6 - Prob. 31WECh. 9.6 - Prob. 32WECh. 9.6 - Prob. 1EXCh. 9.6 - Prob. 2EXCh. 9.6 - Prob. 3EXCh. 9.7 - Prob. 1CECh. 9.7 - Prob. 2CECh. 9.7 - Prob. 3CECh. 9.7 - Prob. 4CECh. 9.7 - Prob. 5CECh. 9.7 - Prob. 6CECh. 9.7 - Prob. 7CECh. 9.7 - Prob. 1WECh. 9.7 - Prob. 2WECh. 9.7 - Prob. 3WECh. 9.7 - Prob. 4WECh. 9.7 - Prob. 5WECh. 9.7 - Prob. 6WECh. 9.7 - Prob. 7WECh. 9.7 - Prob. 8WECh. 9.7 - Prob. 9WECh. 9.7 - Prob. 10WECh. 9.7 - Prob. 11WECh. 9.7 - Prob. 12WECh. 9.7 - Prob. 13WECh. 9.7 - Prob. 14WECh. 9.7 - Prob. 15WECh. 9.7 - Prob. 16WECh. 9.7 - Prob. 17WECh. 9.7 - Prob. 18WECh. 9.7 - Prob. 19WECh. 9.7 - Prob. 20WECh. 9.7 - Prob. 21WECh. 9.7 - Prob. 22WECh. 9.7 - Prob. 23WECh. 9.7 - Prob. 24WECh. 9.7 - Prob. 25WECh. 9.7 - Prob. 26WECh. 9.7 - Prob. 27WECh. 9.7 - Prob. 28WECh. 9.7 - Prob. 1ST2Ch. 9.7 - Prob. 2ST2Ch. 9.7 - Prob. 3ST2Ch. 9.7 - Prob. 4ST2Ch. 9.7 - Prob. 5ST2Ch. 9.7 - Prob. 6ST2Ch. 9.7 - Prob. 7ST2Ch. 9.7 - Prob. 8ST2Ch. 9.7 - Prob. 1ECh. 9.7 - Prob. 2ECh. 9.7 - Prob. 3ECh. 9.7 - Prob. 4ECh. 9.7 - Prob. 5ECh. 9 - Prob. 1CRCh. 9 - Prob. 2CRCh. 9 - Prob. 3CRCh. 9 - Prob. 4CRCh. 9 - Prob. 5CRCh. 9 - Prob. 6CRCh. 9 - Prob. 7CRCh. 9 - Prob. 8CRCh. 9 - Prob. 9CRCh. 9 - Prob. 10CRCh. 9 - Prob. 11CRCh. 9 - Prob. 12CRCh. 9 - Prob. 13CRCh. 9 - Prob. 14CRCh. 9 - Prob. 15CRCh. 9 - Prob. 16CRCh. 9 - Prob. 17CRCh. 9 - Prob. 18CRCh. 9 - Prob. 19CRCh. 9 - Prob. 20CRCh. 9 - Prob. 21CRCh. 9 - Prob. 22CRCh. 9 - Prob. 23CRCh. 9 - Prob. 24CRCh. 9 - Prob. 1CTCh. 9 - Prob. 2CTCh. 9 - Prob. 3CTCh. 9 - Prob. 4CTCh. 9 - Prob. 5CTCh. 9 - Prob. 6CTCh. 9 - Prob. 7CTCh. 9 - Prob. 8CTCh. 9 - Prob. 9CTCh. 9 - Prob. 10CTCh. 9 - Prob. 11CTCh. 9 - Prob. 12CTCh. 9 - Prob. 13CTCh. 9 - Prob. 14CTCh. 9 - Prob. 15CTCh. 9 - Prob. 16CTCh. 9 - Prob. 17CTCh. 9 - Prob. 18CTCh. 9 - Prob. 1CURCh. 9 - Prob. 2CURCh. 9 - Prob. 3CURCh. 9 - Prob. 4CURCh. 9 - Prob. 5CURCh. 9 - Prob. 6CURCh. 9 - Prob. 7CURCh. 9 - Prob. 8CURCh. 9 - Prob. 9CURCh. 9 - Prob. 10CURCh. 9 - Prob. 11CURCh. 9 - Prob. 12CURCh. 9 - Prob. 13CURCh. 9 - Prob. 14CURCh. 9 - Prob. 15CURCh. 9 - Prob. 16CURCh. 9 - Prob. 17CURCh. 9 - Prob. 18CURCh. 9 - Prob. 19CURCh. 9 - Prob. 20CURCh. 9 - Prob. 21CURCh. 9 - Prob. 22CURCh. 9 - Prob. 23CURCh. 9 - Prob. 24CURCh. 9 - Prob. 25CURCh. 9 - Prob. 26CURCh. 9 - Prob. 27CURCh. 9 - Prob. 28CURCh. 9 - Prob. 29CURCh. 9 - Prob. 30CUR
Additional Math Textbook Solutions
Find more solutions based on key concepts
The lateral and surface area of the prism.
Pre-Algebra Student Edition
Replace the polar equations in Exercises 27–52 with equivalent Cartesian equations. Then describe or identify t...
University Calculus: Early Transcendentals (4th Edition)
Testing Hypotheses. In Exercises 13-24, assume that a simple random sample has been selected and test the given...
Elementary Statistics (13th Edition)
3. Voluntary Response Sample What is a voluntary response sample, and why is such a sample generally not suitab...
Elementary Statistics
A linear equation is solved by using the intersection of graphs method. Find the solution by interpreting the g...
College Algebra with Modeling & Visualization (5th Edition)
Knowledge Booster
Similar questions
- Classwork for Geometry 1st X S Savvas Realize * MARYIA DASHUTSINA-Ba → CA savvasrealize.com/dashboard/classes/49ec9fc00d8f48ec9a4b05b30c9ee0ba A > SIS © = =Wauconda Middle S... 31 WMS 8th Grade Tea... SIS Grades and Attenda.... esc GEOMETRY 1ST < Study Guide T6 K 18 L 63° 9 N M Quadrilateral JKLM is a parallelogram. What is the m ZKJN? mZKJN = Review Progress acerarrow_forwardWhy is this proof incorrect? State what statement and/or reason is incorrect and why. Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: Angle 3 is congruent to angle 5 Why is this proof incorrect? Statements Reasons 1. Overline OR is congruent to overline OQ, angle N is congruent to angle P 1. Given 2. Overline ON is congruent to overline OP 2. Converse of the Isosceles Triangle Theorem 3. Triangle ONR is congruent to triangle OPQ 3. SAS 4. Angle 3 is congruent to angle 5 4. CPCTCarrow_forwardGiven: AABE ~ ACDE. Prove: AC bisects BD. Note: quadrilateral properties are not permitted in this proof. Step Statement Reason AABE ACDE Given 2 ZDEC ZAEB Vertical angles are congruent try Type of Statement A E B D Carrow_forward
- 2) Based on the given information and the diagram, a. Which congruence statements can be proven? Select all that apply.Given: Overline OR is congruent to overline OQ, angle N is congruent to angle PProve: angle 3 is congruent to angle 5A. Overline ON is congruent to overline OPB. Angle 1 is congruent to angle 2C. Overline ON is congruent to overline OR and overline OP is congruent to overine OQD. angle 1 is congruent to angle 3 and angle 2 is congruent to angle 5There are more than one correct answerarrow_forwardnt/Ray Skew Lines/ J K # H L 艹 G C D E F Diagrams m Three Points th a Protractor Answer Attempt 3 out of 3 el 1 is congruent to Submit Answer 103 Log Out REE Young the → C # $arrow_forward4:54 PM Thu Jan 16 cdn.assess.prod.mheducation.com Question 3 The angle bisectors of APQR are PZ, QZ, and RZ. They meet at a single point Z. (In other words, Z is the incenter of APQR.) Suppose YZ = 22, QZ = 23, mz WPY 38°, and mzXQZ = 54°. Find the following measures. Note that the figure is not drawn to scale. P W Z X R Y mzXQW WZ = = 0 mz XRZ = 0°arrow_forward
- Ja дх dx dx Q3: Define the linear functional J: H()-R by تاریخ (v) = ½a(v, v) - (v) == Let u be the unique weak solution to a(u,v) = L(v) in H₁(2) and suppose that a(...) is a symmetric bilinear form on H() prove that a Buy v) = 1- u is minimizer. 2- u is unique. 3- The minimizer J(u,) can be rewritten under J(u)=u' Au-ub, algebraic form Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer only 1-show that thelation to -Auf in N, u = 0 on a satisfies the stability Vulf and show that V(u-u,)||² = ||vu||2 - ||vu||2 lu-ulls Chu||2 2- Prove that Where =1 ||ul|= a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinear form a(u, v) = (Au, Av) + (Vu, Vv) + (Vu, v) + (u, v) Show that a(u, v) continues and V- elliptic on H(2) (3) (0.0), (3.0)arrow_forwardQ1: A) fill the following: 1- The number of triangular in a triangular region with 5 nodes is quadrilateral with n=5 and m=6 nodés is 2- The complex shape function in 1-D 3- dim(P4(K))=- (7M --- and in the and multiplex shape function in 2-D is 4- The trial space and test space for problem -Auf, u = go on and B) Define the energy norm and prove that the solution u, defined by Galerkin orthogonal satisfies the best approximation. Q2: A) Find the varitional form for the problem 1330 (b(x)) - x²=0, 0arrow_forwardcould you help?arrow_forward(ii)arrow_forwardA convex polygon is said to be regular if all of its sides have the same length and all angles between sides are the same. Let Pr denote the regular convex n-sided polygon. Thus, P3 is the equilateral triangle, P₁ is the square, P is the pentagon etc. Compute a formula for the size of any internal angle of Pn.arrow_forward+ Recall that a map, f: R2 R², is an isometry if |P-Q| = |ƒ(P) — ƒ (Q) for all pairs of points P and Q in R². Thus, f is a distance preserving map. Show that an isometry, f: R² → R² also preserves angles. In other words if two line segments meeting at a point determine an angle a, their image line segments meeting at the image of that point also determine the angle a.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning