McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 9.5, Problem 24WE
a.
To determine
To find:The reason thatthe numbered
a.
Expert Solution
Answer to Problem 24WE
Numbered angles are congruent because their corresponding arcs are also congruent.
Explanation of Solution
Giveninformation: A regular polygon with 7 sides is given as shown in below figure,
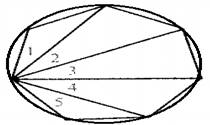
Concept used:Use following properties of a
(i) By theorem 9.4, congruent chords have congruent arcs.
(ii) In a circle, congruent arcs subtend congruent inscribed angles on their remaining arcs.
To prove: In given figure, all number angles are congruent.
Key steps of proof of case III:
- Circumscribe a circle along given regular polygon with 7 sides.
- Thus, congruent sides of regular polygon are congruent chords of this circle.
- By above (i) concept, their corresponding arcs are also congruent.
- Now as these congruent arcs make numbered inscribed angles, by above concept (ii), these numbered angles will also be congruent.
Conclusion: Thus,It concludes that all numbered angles are congruent as their corresponding arcs of circumscribed circle are also congruent.
b.
To determine
To find:If angles inscribed by arcs of a regular polygon are congruent, irrespective of its total sides in it.
b.
Expert Solution
Answer to Problem 24WE
In a regular polygon of any number of sides, the inscribed angles by its arcs are always congruent.
Explanation of Solution
Giveninformation: A regular polygon with 7 sides is given as shown in below figure,
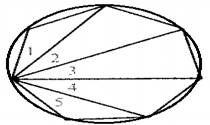
Concept used:Use following properties of a circle,
(i) By theorem 9.4, congruent chords have congruent arcs.
(ii) In a circle, congruent arcs subtend congruent inscribed angles on their remaining arcs.
To prove: If result of part (a) is applicable to a regular polygon with any number of its sides.
Key steps of proof of case III:
- Circumscribe a circle along a regular polygon with any number of sides.
- Thus, congruent sides of regular polygon are congruent chords of this circle.
- By above (i) concept, their corresponding arcs are also congruent.
- Now as these congruent arcs make numbered inscribed angles, by above concept (ii), these numbered angles will also be congruent.
Conclusion: Thus, It concludes that all numbered angles are congruent as their corresponding arcs of circumscribed circle are also congruent. And it does not depend on number of sides of the regular polygon.
Chapter 9 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 9.1 - Prob. 1CECh. 9.1 - Prob. 2CECh. 9.1 - Prob. 3CECh. 9.1 - Prob. 4CECh. 9.1 - Prob. 5CECh. 9.1 - Prob. 6CECh. 9.1 - Prob. 7CECh. 9.1 - Prob. 8CECh. 9.1 - Prob. 9CECh. 9.1 - Prob. 10CE
Ch. 9.1 - Prob. 11CECh. 9.1 - Prob. 1WECh. 9.1 - Prob. 2WECh. 9.1 - Prob. 3WECh. 9.1 - Prob. 4WECh. 9.1 - Prob. 5WECh. 9.1 - Prob. 6WECh. 9.1 - Prob. 7WECh. 9.1 - Prob. 8WECh. 9.1 - Prob. 9WECh. 9.1 - Prob. 10WECh. 9.1 - Prob. 11WECh. 9.1 - Prob. 12WECh. 9.1 - Prob. 13WECh. 9.1 - Prob. 14WECh. 9.1 - Prob. 15WECh. 9.1 - Prob. 16WECh. 9.1 - Prob. 17WECh. 9.1 - Prob. 18WECh. 9.1 - Prob. 19WECh. 9.1 - Prob. 20WECh. 9.1 - Prob. 1ECh. 9.1 - Prob. 2ECh. 9.1 - Prob. 3ECh. 9.1 - Prob. 4ECh. 9.1 - Prob. 5ECh. 9.2 - Prob. 1CECh. 9.2 - Prob. 2CECh. 9.2 - Prob. 3CECh. 9.2 - Prob. 4CECh. 9.2 - Prob. 5CECh. 9.2 - Prob. 1WECh. 9.2 - Prob. 2WECh. 9.2 - Prob. 3WECh. 9.2 - Prob. 4WECh. 9.2 - Prob. 5WECh. 9.2 - Prob. 6WECh. 9.2 - Prob. 7WECh. 9.2 - Prob. 8WECh. 9.2 - Prob. 9WECh. 9.2 - Prob. 10WECh. 9.2 - Prob. 11WECh. 9.2 - Prob. 12WECh. 9.2 - Prob. 13WECh. 9.2 - Prob. 14WECh. 9.2 - Prob. 15WECh. 9.2 - Prob. 16WECh. 9.2 - Prob. 17WECh. 9.2 - Prob. 18WECh. 9.2 - Prob. 19WECh. 9.2 - Prob. 20WECh. 9.2 - Prob. 21WECh. 9.2 - Prob. 22WECh. 9.2 - Prob. 23WECh. 9.2 - Prob. 1MRECh. 9.2 - Prob. 2MRECh. 9.2 - Prob. 3MRECh. 9.3 - Prob. 1CECh. 9.3 - Prob. 2CECh. 9.3 - Prob. 3CECh. 9.3 - Prob. 4CECh. 9.3 - Prob. 5CECh. 9.3 - Prob. 6CECh. 9.3 - Prob. 7CECh. 9.3 - Prob. 8CECh. 9.3 - Prob. 9CECh. 9.3 - Prob. 10CECh. 9.3 - Prob. 11CECh. 9.3 - Prob. 12CECh. 9.3 - Prob. 13CECh. 9.3 - Prob. 1WECh. 9.3 - Prob. 2WECh. 9.3 - Prob. 3WECh. 9.3 - Prob. 4WECh. 9.3 - Prob. 5WECh. 9.3 - Prob. 6WECh. 9.3 - Prob. 7WECh. 9.3 - Prob. 8WECh. 9.3 - Prob. 9WECh. 9.3 - Prob. 10WECh. 9.3 - Prob. 11WECh. 9.3 - Prob. 12WECh. 9.3 - Prob. 13WECh. 9.3 - Prob. 14WECh. 9.3 - Prob. 15WECh. 9.3 - Prob. 16WECh. 9.3 - Prob. 17WECh. 9.3 - Prob. 18WECh. 9.3 - Prob. 19WECh. 9.3 - Prob. 20WECh. 9.3 - Prob. 21WECh. 9.3 - Prob. 22WECh. 9.3 - Prob. 23WECh. 9.3 - Prob. 24WECh. 9.4 - Prob. 1CECh. 9.4 - Prob. 2CECh. 9.4 - Prob. 3CECh. 9.4 - Prob. 4CECh. 9.4 - Prob. 5CECh. 9.4 - Prob. 6CECh. 9.4 - Prob. 7CECh. 9.4 - Prob. 1WECh. 9.4 - Prob. 2WECh. 9.4 - Prob. 3WECh. 9.4 - Prob. 4WECh. 9.4 - Prob. 5WECh. 9.4 - Prob. 6WECh. 9.4 - Prob. 7WECh. 9.4 - Prob. 8WECh. 9.4 - Prob. 9WECh. 9.4 - Prob. 10WECh. 9.4 - Prob. 11WECh. 9.4 - Prob. 12WECh. 9.4 - Prob. 13WECh. 9.4 - Prob. 14WECh. 9.4 - Prob. 15WECh. 9.4 - Prob. 16WECh. 9.4 - Prob. 17WECh. 9.4 - Prob. 18WECh. 9.4 - Prob. 19WECh. 9.4 - Prob. 20WECh. 9.4 - Prob. 21WECh. 9.4 - Prob. 22WECh. 9.4 - Prob. 23WECh. 9.4 - Prob. 24WECh. 9.4 - Prob. 25WECh. 9.4 - Prob. 26WECh. 9.4 - Prob. 27WECh. 9.4 - Prob. 1ST1Ch. 9.4 - Prob. 2ST1Ch. 9.4 - Prob. 3ST1Ch. 9.4 - Prob. 4ST1Ch. 9.4 - Prob. 5ST1Ch. 9.4 - Prob. 6ST1Ch. 9.5 - Prob. 1CECh. 9.5 - Prob. 2CECh. 9.5 - Prob. 3CECh. 9.5 - Prob. 4CECh. 9.5 - Prob. 5CECh. 9.5 - Prob. 6CECh. 9.5 - Prob. 7CECh. 9.5 - Prob. 8CECh. 9.5 - Prob. 9CECh. 9.5 - Prob. 10CECh. 9.5 - Prob. 11CECh. 9.5 - Prob. 12CECh. 9.5 - Prob. 13CECh. 9.5 - Prob. 14CECh. 9.5 - Prob. 1WECh. 9.5 - Prob. 2WECh. 9.5 - Prob. 3WECh. 9.5 - Prob. 4WECh. 9.5 - Prob. 5WECh. 9.5 - Prob. 6WECh. 9.5 - Prob. 7WECh. 9.5 - Prob. 8WECh. 9.5 - Prob. 9WECh. 9.5 - Prob. 10WECh. 9.5 - Prob. 11WECh. 9.5 - Prob. 12WECh. 9.5 - Prob. 13WECh. 9.5 - Prob. 14WECh. 9.5 - Prob. 15WECh. 9.5 - Prob. 16WECh. 9.5 - Prob. 17WECh. 9.5 - Prob. 18WECh. 9.5 - Prob. 19WECh. 9.5 - Prob. 20WECh. 9.5 - Prob. 21WECh. 9.5 - Prob. 22WECh. 9.5 - Prob. 23WECh. 9.5 - Prob. 24WECh. 9.5 - Prob. 25WECh. 9.5 - Prob. 26WECh. 9.5 - Prob. 27WECh. 9.5 - Prob. 28WECh. 9.5 - Prob. 29WECh. 9.5 - Prob. 1MRECh. 9.5 - Prob. 2MRECh. 9.5 - Prob. 3MRECh. 9.5 - Prob. 4MRECh. 9.5 - Prob. 5MRECh. 9.5 - Prob. 6MRECh. 9.6 - Prob. 1CECh. 9.6 - Prob. 2CECh. 9.6 - Prob. 3CECh. 9.6 - Prob. 4CECh. 9.6 - Prob. 5CECh. 9.6 - Prob. 6CECh. 9.6 - Prob. 7CECh. 9.6 - Prob. 8CECh. 9.6 - Prob. 9CECh. 9.6 - Prob. 10CECh. 9.6 - Prob. 1WECh. 9.6 - Prob. 2WECh. 9.6 - Prob. 3WECh. 9.6 - Prob. 4WECh. 9.6 - Prob. 5WECh. 9.6 - Prob. 6WECh. 9.6 - Prob. 7WECh. 9.6 - Prob. 8WECh. 9.6 - Prob. 9WECh. 9.6 - Prob. 10WECh. 9.6 - Prob. 11WECh. 9.6 - Prob. 12WECh. 9.6 - Prob. 13WECh. 9.6 - Prob. 14WECh. 9.6 - Prob. 15WECh. 9.6 - Prob. 16WECh. 9.6 - Prob. 17WECh. 9.6 - Prob. 18WECh. 9.6 - Prob. 19WECh. 9.6 - Prob. 20WECh. 9.6 - Prob. 21WECh. 9.6 - Prob. 22WECh. 9.6 - Prob. 23WECh. 9.6 - Prob. 24WECh. 9.6 - Prob. 25WECh. 9.6 - Prob. 26WECh. 9.6 - Prob. 27WECh. 9.6 - Prob. 28WECh. 9.6 - Prob. 29WECh. 9.6 - Prob. 30WECh. 9.6 - Prob. 31WECh. 9.6 - Prob. 32WECh. 9.6 - Prob. 1EXCh. 9.6 - Prob. 2EXCh. 9.6 - Prob. 3EXCh. 9.7 - Prob. 1CECh. 9.7 - Prob. 2CECh. 9.7 - Prob. 3CECh. 9.7 - Prob. 4CECh. 9.7 - Prob. 5CECh. 9.7 - Prob. 6CECh. 9.7 - Prob. 7CECh. 9.7 - Prob. 1WECh. 9.7 - Prob. 2WECh. 9.7 - Prob. 3WECh. 9.7 - Prob. 4WECh. 9.7 - Prob. 5WECh. 9.7 - Prob. 6WECh. 9.7 - Prob. 7WECh. 9.7 - Prob. 8WECh. 9.7 - Prob. 9WECh. 9.7 - Prob. 10WECh. 9.7 - Prob. 11WECh. 9.7 - Prob. 12WECh. 9.7 - Prob. 13WECh. 9.7 - Prob. 14WECh. 9.7 - Prob. 15WECh. 9.7 - Prob. 16WECh. 9.7 - Prob. 17WECh. 9.7 - Prob. 18WECh. 9.7 - Prob. 19WECh. 9.7 - Prob. 20WECh. 9.7 - Prob. 21WECh. 9.7 - Prob. 22WECh. 9.7 - Prob. 23WECh. 9.7 - Prob. 24WECh. 9.7 - Prob. 25WECh. 9.7 - Prob. 26WECh. 9.7 - Prob. 27WECh. 9.7 - Prob. 28WECh. 9.7 - Prob. 1ST2Ch. 9.7 - Prob. 2ST2Ch. 9.7 - Prob. 3ST2Ch. 9.7 - Prob. 4ST2Ch. 9.7 - Prob. 5ST2Ch. 9.7 - Prob. 6ST2Ch. 9.7 - Prob. 7ST2Ch. 9.7 - Prob. 8ST2Ch. 9.7 - Prob. 1ECh. 9.7 - Prob. 2ECh. 9.7 - Prob. 3ECh. 9.7 - Prob. 4ECh. 9.7 - Prob. 5ECh. 9 - Prob. 1CRCh. 9 - Prob. 2CRCh. 9 - Prob. 3CRCh. 9 - Prob. 4CRCh. 9 - Prob. 5CRCh. 9 - Prob. 6CRCh. 9 - Prob. 7CRCh. 9 - Prob. 8CRCh. 9 - Prob. 9CRCh. 9 - Prob. 10CRCh. 9 - Prob. 11CRCh. 9 - Prob. 12CRCh. 9 - Prob. 13CRCh. 9 - Prob. 14CRCh. 9 - Prob. 15CRCh. 9 - Prob. 16CRCh. 9 - Prob. 17CRCh. 9 - Prob. 18CRCh. 9 - Prob. 19CRCh. 9 - Prob. 20CRCh. 9 - Prob. 21CRCh. 9 - Prob. 22CRCh. 9 - Prob. 23CRCh. 9 - Prob. 24CRCh. 9 - Prob. 1CTCh. 9 - Prob. 2CTCh. 9 - Prob. 3CTCh. 9 - Prob. 4CTCh. 9 - Prob. 5CTCh. 9 - Prob. 6CTCh. 9 - Prob. 7CTCh. 9 - Prob. 8CTCh. 9 - Prob. 9CTCh. 9 - Prob. 10CTCh. 9 - Prob. 11CTCh. 9 - Prob. 12CTCh. 9 - Prob. 13CTCh. 9 - Prob. 14CTCh. 9 - Prob. 15CTCh. 9 - Prob. 16CTCh. 9 - Prob. 17CTCh. 9 - Prob. 18CTCh. 9 - Prob. 1CURCh. 9 - Prob. 2CURCh. 9 - Prob. 3CURCh. 9 - Prob. 4CURCh. 9 - Prob. 5CURCh. 9 - Prob. 6CURCh. 9 - Prob. 7CURCh. 9 - Prob. 8CURCh. 9 - Prob. 9CURCh. 9 - Prob. 10CURCh. 9 - Prob. 11CURCh. 9 - Prob. 12CURCh. 9 - Prob. 13CURCh. 9 - Prob. 14CURCh. 9 - Prob. 15CURCh. 9 - Prob. 16CURCh. 9 - Prob. 17CURCh. 9 - Prob. 18CURCh. 9 - Prob. 19CURCh. 9 - Prob. 20CURCh. 9 - Prob. 21CURCh. 9 - Prob. 22CURCh. 9 - Prob. 23CURCh. 9 - Prob. 24CURCh. 9 - Prob. 25CURCh. 9 - Prob. 26CURCh. 9 - Prob. 27CURCh. 9 - Prob. 28CURCh. 9 - Prob. 29CURCh. 9 - Prob. 30CUR
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Exercises 11-20, express each decimal as a percent.
11. 0.59
Thinking Mathematically (6th Edition)
In track, the second lane from the inside of the track is longer than the inside lane. Use this information to ...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
1. combination of numbers, variables, and operation symbols is called an algebraic______.
Algebra and Trigonometry (6th Edition)
Interpreting a P-Value In Exercises 3–8, the P-value for a hypothesis test is shown. Use the P-value to decide ...
Elementary Statistics: Picturing the World (7th Edition)
Find the point-slope form of the line passing through the given points. Use the first point as (x1, .y1). Plot ...
College Algebra with Modeling & Visualization (5th Edition)
For years, telephone area codes in the United States and Canada consisted of a sequence of three digits. The fi...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Please help me answer this question!. Please handwrite it. I don't require AI answers. Thanks for your time!.arrow_forward1 What is the area of triangle ABC? 12 60° 60° A D B A 6√√3 square units B 18√3 square units 36√3 square units D 72√3 square unitsarrow_forwardPar quel quadrilatère est-elle représentée sur ce besoin en perspective cavalièrearrow_forward
- -10 M 10 y 5 P -5 R 5 -5 Ο 10 N -10 Οarrow_forwardDescribe enlargement on map gridarrow_forward◆ Switch To Light Mode HOMEWORK: 18, 19, 24, 27, 29 ***Please refer to the HOMEWORK sheet from Thursday, 9/14, for the problems ****Please text or email me if you have any questions 18. Figure 5-35 is a map of downtown Royalton, showing the Royalton River running through the downtown area and the three islands (A, B, and C) connected to each other and both banks by eight bridges. The Down- town Athletic Club wants to design the route for a marathon through the downtown area. Draw a graph that models the layout of Royalton. FIGURE 5-35 North Royalton Royalton River South Royption 19. A night watchman must walk the streets of the Green Hills subdivision shown in Fig. 5-36. The night watch- man needs to walk only once along each block. Draw a graph that models this situation.arrow_forward
- Solve this question and check if my answer provided is correctarrow_forwardProof: LN⎯⎯⎯⎯⎯LN¯ divides quadrilateral KLMN into two triangles. The sum of the angle measures in each triangle is ˚, so the sum of the angle measures for both triangles is ˚. So, m∠K+m∠L+m∠M+m∠N=m∠K+m∠L+m∠M+m∠N=˚. Because ∠K≅∠M∠K≅∠M and ∠N≅∠L, m∠K=m∠M∠N≅∠L, m∠K=m∠M and m∠N=m∠Lm∠N=m∠L by the definition of congruence. By the Substitution Property of Equality, m∠K+m∠L+m∠K+m∠L=m∠K+m∠L+m∠K+m∠L=°,°, so (m∠K)+ m∠K+ (m∠L)= m∠L= ˚. Dividing each side by gives m∠K+m∠L=m∠K+m∠L= °.°. The consecutive angles are supplementary, so KN⎯⎯⎯⎯⎯⎯∥LM⎯⎯⎯⎯⎯⎯KN¯∥LM¯ by the Converse of the Consecutive Interior Angles Theorem. Likewise, (m∠K)+m∠K+ (m∠N)=m∠N= ˚, or m∠K+m∠N=m∠K+m∠N= ˚. So these consecutive angles are supplementary and KL⎯⎯⎯⎯⎯∥NM⎯⎯⎯⎯⎯⎯KL¯∥NM¯ by the Converse of the Consecutive Interior Angles Theorem. Opposite sides are parallel, so quadrilateral KLMN is a parallelogram.arrow_forwardQuadrilateral BCDE is similar to quadrilateral FGHI. Find the measure of side FG. Round your answer to the nearest tenth if necessary. BCDEFGHI2737.55arrow_forward
- An angle measures 70.6° more than the measure of its supplementary angle. What is the measure of each angle?arrow_forwardName: Date: Per: Unit 7: Geometry Homework 4: Parallel Lines & Transversals **This is a 2-page document! ** Directions: Classify each angle pair and indicate whether they are congruent or supplementary. 1 1.23 and 25 2. 24 and 28 3. 22 and 25 4. 22 and 28 5. 21 and 27 6. 22 and 26 Directions: Find each angle measure. 7. Given: wvm25-149 m21- 8. Given: mn: m1=74 mz2- m22- m.23- m23- mz4= V mz4= m25= m26- m26= m27- m27 m28- m48= 9. Given: a || b: m28 125 m2- 10. Given: xy: m22-22 m21- = mz2- m43- m3- mZA m24-> m. 5- m25- m26- m.26=> m2]=> m27= m28- 11. Given: rm2-29: m15-65 m2=> m29-> m3- m. 10- mc4= m25= m212- m.46- m213- mat- m214- m28- & Gina when (N) Things ALICE 2017arrow_forwardMatch each statement to the set of shapes that best describes them. 1. Similar triangles by SSS 2. Similar triangles by SAS 3. Similar triangles by AA 4. The triangles are not similar > U E 35° 89° S F 89° J 35° 94° G 52° 90° E K 52° Iarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Maths - Geometry - What is an Angle - English; Author: Bodhaguru;https://www.youtube.com/watch?v=bsuDcCjFq6c;License: Standard YouTube License, CC-BY
What is an Angle? | Different Types of Angles | Geometry | Math | LetsTute; Author: Let'stute;https://www.youtube.com/watch?v=aGejx2fRCHU;License: Standard Youtube License