Vector Mechanics for Engineers: Statics and Dynamics
11th Edition
ISBN: 9780073398242
Author: Ferdinand P. Beer, E. Russell Johnston Jr., David Mazurek, Phillip J. Cornwell, Brian Self
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 9.5, Problem 9.147P
The figure shown is formed of
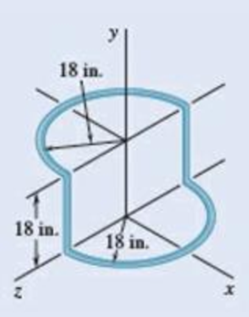
Fig. P9.147
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Problem 09.086 - Orientation of the principal axes and the corresponding moments of inertia
For the area indicated, determine the orientation of the principal axes at the origin and the corresponding values of the moments of
inertia when b= 76 mm and h = 56 mm.
b
The value of mis
The value of 0m2 is
The value of Imax is
The value of I min is
180
270
1.429
7292
×
h
x
106 mm4.
106 mm4
A farmer constructs a trough by welding a rectangular piece of 2-mm-thick sheet steel to half of a steel drum. Knowing that the density of steel is 7850 kg/m3 and that the thickness of the walls of the drum is 1.8 mm, determine the mass moment of inertia of the trough with respect to each of the coordinate axes. Neglect the mass of the welds.
Please help me answer the following, thanks.
Chapter 9 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
Ch. 9.1 - 9.1 through 9.4 Determine by direct integration...Ch. 9.1 - 9.1 through 9.4 Determine by direct integration...Ch. 9.1 - Prob. 9.3PCh. 9.1 - Prob. 9.4PCh. 9.1 - 9.5 through 9.8 Determine by direct integration...Ch. 9.1 - 9.5 through 9.8 Determine by direct integration...Ch. 9.1 - Prob. 9.7PCh. 9.1 - Prob. 9.8PCh. 9.1 - 9.9 through 9.11 Determine by direct integration...Ch. 9.1 - Prob. 9.10P
Ch. 9.1 - Prob. 9.11PCh. 9.1 - Prob. 9.12PCh. 9.1 - Prob. 9.13PCh. 9.1 - 9.12 through 9.14 Determine by direct integration...Ch. 9.1 - Prob. 9.15PCh. 9.1 - Prob. 9.16PCh. 9.1 - Prob. 9.17PCh. 9.1 - Prob. 9.18PCh. 9.1 - Prob. 9.19PCh. 9.1 - Prob. 9.20PCh. 9.1 - Prob. 9.21PCh. 9.1 - Prob. 9.22PCh. 9.1 - Prob. 9.23PCh. 9.1 - 9.23 and 9.24 Determine the polar moment of...Ch. 9.1 - Prob. 9.25PCh. 9.1 - Prob. 9.26PCh. 9.1 - Prob. 9.27PCh. 9.1 - Prob. 9.28PCh. 9.1 - Prob. 9.29PCh. 9.1 - Prove that the centroidal polar moment of inertia...Ch. 9.2 - Prob. 9.31PCh. 9.2 - Prob. 9.32PCh. 9.2 - Prob. 9.33PCh. 9.2 - Prob. 9.34PCh. 9.2 - Prob. 9.35PCh. 9.2 - Prob. 9.36PCh. 9.2 - Prob. 9.37PCh. 9.2 - Prob. 9.38PCh. 9.2 - Prob. 9.39PCh. 9.2 - Prob. 9.40PCh. 9.2 - Prob. 9.41PCh. 9.2 - 9.41 through 9.44 Determine the moments of inertia...Ch. 9.2 - Prob. 9.43PCh. 9.2 - Prob. 9.44PCh. 9.2 - 9.45 and 9.46 Determine the polar moment of...Ch. 9.2 - Prob. 9.46PCh. 9.2 - Prob. 9.47PCh. 9.2 - 9.47 and 9.48 Determine the polar moment of...Ch. 9.2 - 9.49 Two channels and two plates are used to form...Ch. 9.2 - Prob. 9.50PCh. 9.2 - Prob. 9.51PCh. 9.2 - Two 20-mm steel plates are welded to a rolled S...Ch. 9.2 - A channel and a plate are welded together as shown...Ch. 9.2 - Prob. 9.54PCh. 9.2 - Two L76 76 6.4-mm angles are welded to a C250 ...Ch. 9.2 - Prob. 9.56PCh. 9.2 - Prob. 9.57PCh. 9.2 - 9.57 and 9.58 The panel shown forms the end of a...Ch. 9.2 - Prob. 9.59PCh. 9.2 - 9.60 The panel shown forms the end of a trough...Ch. 9.2 - Prob. 9.61PCh. 9.2 - Prob. 9.62PCh. 9.2 - Prob. 9.63PCh. 9.2 - Prob. 9.64PCh. 9.2 - Prob. 9.65PCh. 9.2 - Prob. 9.66PCh. 9.3 - 9.67 through 9.70 Determine by direct integration...Ch. 9.3 - Prob. 9.68PCh. 9.3 - Prob. 9.69PCh. 9.3 - Prob. 9.70PCh. 9.3 - Prob. 9.71PCh. 9.3 - Prob. 9.72PCh. 9.3 - Prob. 9.73PCh. 9.3 - 9.71 through 9.74 Using the parallel-axis theorem,...Ch. 9.3 - Prob. 9.75PCh. 9.3 - 9.75 through 9.78 Using the parallel-axis theorem,...Ch. 9.3 - Prob. 9.77PCh. 9.3 - Prob. 9.78PCh. 9.3 - Determine for the quarter ellipse of Prob. 9.67...Ch. 9.3 - Determine the moments of inertia and the product...Ch. 9.3 - Determine the moments of inertia and the product...Ch. 9.3 - 9.75 through 9.78 Using the parallel-axis theorem,...Ch. 9.3 - Determine the moments of inertia and the product...Ch. 9.3 - Determine the moments of inertia and the product...Ch. 9.3 - Prob. 9.85PCh. 9.3 - 9.86 through 9.88 For the area indicated,...Ch. 9.3 - Prob. 9.87PCh. 9.3 - Prob. 9.88PCh. 9.3 - Prob. 9.89PCh. 9.3 - 9.89 and 9.90 For the angle cross section...Ch. 9.4 - Using Mohrs circle, determine for the quarter...Ch. 9.4 - Using Mohrs circle, determine the moments of...Ch. 9.4 - Prob. 9.93PCh. 9.4 - Using Mohrs circle, determine the moments of...Ch. 9.4 - Using Mohrs circle, determine the moments of...Ch. 9.4 - Using Mohrs circle, determine the moments of...Ch. 9.4 - For the quarter ellipse of Prob. 9.67, use Mohrs...Ch. 9.4 - 9.98 though 9.102 Using Mohrs circle, determine...Ch. 9.4 - Prob. 9.99PCh. 9.4 - 9.98 though 9.102 Using Mohrs circle, determine...Ch. 9.4 - Prob. 9.101PCh. 9.4 - Prob. 9.102PCh. 9.4 - Prob. 9.103PCh. 9.4 - 9.104 and 9.105 Using Mohrs circle, determine the...Ch. 9.4 - 9.104 and 9.105 Using Mohrs circle, determine the...Ch. 9.4 - For a given area, the moments of inertia with...Ch. 9.4 - it is known that for a given area Iy = 48 106 mm4...Ch. 9.4 - Prob. 9.108PCh. 9.4 - Prob. 9.109PCh. 9.4 - Prob. 9.110PCh. 9.5 - A thin plate with a mass m is cut in the shape of...Ch. 9.5 - A ring with a mass m is cut from a thin uniform...Ch. 9.5 - Prob. 9.113PCh. 9.5 - The parabolic spandrel shown was cut from a thin,...Ch. 9.5 - Prob. 9.115PCh. 9.5 - Fig. P9.115 and P9.116 9.116 A piece of thin,...Ch. 9.5 - 9.117 A thin plate with a mass m has the...Ch. 9.5 - Prob. 9.118PCh. 9.5 - 9.119 Determine by direct integration the mass...Ch. 9.5 - The area shown is revolved about the x axis to...Ch. 9.5 - 9.121 The area shown is revolved about the x axis...Ch. 9.5 - Prob. 9.122PCh. 9.5 - Prob. 9.123PCh. 9.5 - Prob. 9.124PCh. 9.5 - Prob. 9.125PCh. 9.5 - Prob. 9.126PCh. 9.5 - Prob. 9.127PCh. 9.5 - Prob. 9.128PCh. 9.5 - Prob. 9.129PCh. 9.5 - Prob. 9.130PCh. 9.5 - Prob. 9.131PCh. 9.5 - The cups and the arms of an anemometer are...Ch. 9.5 - Prob. 9.133PCh. 9.5 - Determine the mass moment of inertia of the 0.9-lb...Ch. 9.5 - Prob. 9.135PCh. 9.5 - Prob. 9.136PCh. 9.5 - Prob. 9.137PCh. 9.5 - A section of sheet steel 0.03 in. thick is cut and...Ch. 9.5 - Prob. 9.139PCh. 9.5 - A farmer constructs a trough by welding a...Ch. 9.5 - The machine element shown is fabricated from...Ch. 9.5 - Determine the mass moments of inertia and the...Ch. 9.5 - Determine the mass moment of inertia of the steel...Ch. 9.5 - Prob. 9.144PCh. 9.5 - Determine the mass moment of inertia of the steel...Ch. 9.5 - Aluminum wire with a weight per unit length of...Ch. 9.5 - The figure shown is formed of 18-in.-diameter...Ch. 9.5 - A homogeneous wire with a mass per unit length of...Ch. 9.6 - Determine the mass products of inertia Ixy, Iyz,...Ch. 9.6 - Determine the mass products of inertia Ixy, Iyz,...Ch. 9.6 - Prob. 9.151PCh. 9.6 - Determine the mass products of inertia Ixy, Iyz,...Ch. 9.6 - 9.153 through 9.156 A section of sheet steel 2 mm...Ch. 9.6 - Prob. 9.154PCh. 9.6 - Prob. 9.155PCh. 9.6 - 9.153 through 9.156 A section of sheet steel 2 mm...Ch. 9.6 - Prob. 9.157PCh. 9.6 - Prob. 9.158PCh. 9.6 - Prob. 9.159PCh. 9.6 - Prob. 9.160PCh. 9.6 - Prob. 9.161PCh. 9.6 - For the homogeneous tetrahedron of mass m shown,...Ch. 9.6 - Prob. 9.163PCh. 9.6 - Prob. 9.164PCh. 9.6 - Prob. 9.165PCh. 9.6 - Determine the mass moment of inertia of the steel...Ch. 9.6 - Prob. 9.167PCh. 9.6 - Prob. 9.168PCh. 9.6 - Prob. 9.169PCh. 9.6 - 9.170 through 9.172 For the wire figure of the...Ch. 9.6 - Prob. 9.171PCh. 9.6 - Prob. 9.172PCh. 9.6 - Prob. 9.173PCh. 9.6 - Prob. 9.174PCh. 9.6 - Prob. 9.175PCh. 9.6 - Prob. 9.176PCh. 9.6 - Prob. 9.177PCh. 9.6 - Prob. 9.178PCh. 9.6 - Prob. 9.179PCh. 9.6 - Prob. 9.180PCh. 9.6 - Prob. 9.181PCh. 9.6 - Prob. 9.182PCh. 9.6 - Prob. 9.183PCh. 9.6 - Prob. 9.184PCh. 9 - Determine by direct integration the moments of...Ch. 9 - Determine the moment of inertia and the radius of...Ch. 9 - Prob. 9.187RPCh. 9 - Prob. 9.188RPCh. 9 - Prob. 9.189RPCh. 9 - Two L4 4 12-in. angles are welded to a steel...Ch. 9 - Prob. 9.191RPCh. 9 - Prob. 9.192RPCh. 9 - Prob. 9.193RPCh. 9 - Prob. 9.194RPCh. 9 - Prob. 9.195RPCh. 9 - Determine the mass moment of inertia of the steel...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- B.33 Determine the mass moment of inertia of the steel machine element shown with respect to the axis. (The density of steel is 7850 kg/m³.) 50 mm 50 in 240 mi 360 im 100 mm Fig. PB.32 and PB.33 200 mmarrow_forwardA 2-mm thick piece of sheet steel is cut and bent into the machine component shown. Knowing that the density of steel is 7850 kg/m3 , determine the mass moment of inertia of the component with respect to each of the coordinate axes.arrow_forwardA section of sheet steel 2 mm thick is cut and bent into the machine component shown. Knowing that the density of steel is 7850 kg/m3 , determine the mass products of inertia Ixy, Iyz, and Izx of the component.arrow_forward
- 1.3 cm 1.0 cm -0.5 cm 3.8 cm 0.5 cm AI B 3.6 cm PROBLEM 9.44 Determine the moments of inertia I, and I, of the area shown with respect to centroidal axes respectively parallel and perpendicular to side AB.arrow_forwardTwo steel plates are welded to a rolled W section as indicated. Knowing that the centroidal moments of inertia Ix and Iy of the combined section are equal, determine (a) the distance a, (b) the moments of inertia with respect to the centroidal x and y axes.arrow_forwardh Determine the moment of inertia and radius of gyration of the composite shape with respect to the x- and y-axes knowing that b=4 cm, h = 5 cm, T₁ = 2 cm, and r₁ = 1.333 cm. For the x-axis L₂ = b For the y axis I₂ = k₂ = ky =arrow_forward
- Considering L = 50 + a + 2·b + c {mm}, determine the centroidal coordinate Ycg (location of the x´ axis of the centroid) and the moment of inertia is relative to the X´ axis (IX' , ). Assume a minimum precision of 6 significant figures and present the results of the moments of inertia in scientific notation (1.23456·10n ). (Knowing that a=7, b=1, and c=1.) Ycg = IX, =arrow_forwardB.20 A portion of an 8-in.-long steel rod of diameter 1.50 in. is turned to form the conical section shown. Knowing that the turning process reduces the moment of inertia of the rod with respect to the x axis by 20 percent, de- termine the height h of the cone. Fig. PB.20arrow_forwardIt is known that for a given area Iy = 48 x 106 mm4 and Ixy = -20 x 106 mm4, where the x and y axes are rectangular centroidal axes. If the axis corresponding to the maximum product of inertia is obtained by rotating the x axis 67.5° counterclockwise about C , use Mohr’s circle to determine (a) the moment of inertia Ix of the area, (b) the principal centroidal moments of inertia.arrow_forward
- For items 4 and 5. A thin rectangular plate is welded on the center of the top of a circular cylinder. The mass of the cylinder is 5kg and the mass of the triangular plate is 2kg. Note that the x-axis is located on the centroidal x-axis of the triangular plate. 30cm 26cm 0.1725 m diam. d=7cm X 10cm 4. Which of the following is closest to the moment of inertia of the composite object about the x- axis? 0.208 kg-m^2 5. Which of the following is closest to the radius of gyration of the composite object about the x- axis?arrow_forwardFig. PB.15 B.15 A thin steel wire is bent into the shape shown. Dennting the mass per unit length of the wire by m', determine by direct integration the mo- ment of inertia of the wire with respect to each of the coordinate aves. y=(23_123)32arrow_forward100 mm Problem (3) A 3-mm thick piece of aluminum sheet metal is cut and bent into the machine component shown. The density of aluminum is 2770 kg/m³. Determine the mass moment of inertia of the component with respect to the y-axis. 180 mm 160 mm 240 mm 160 mmarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
moment of inertia; Author: NCERT OFFICIAL;https://www.youtube.com/watch?v=A4KhJYrt4-s;License: Standard YouTube License, CC-BY