Chapter 9.3, Problem 68E

(a)

To determine

To Explain: the state appropriate hypothesis for the retailer’s test.

Answer to Problem 68E

  $H_0:\mu <50$

  $H_1:\mu >50$

Explanation of Solution

Given:

Claim is that mean is bigger than 50%

The null hypothesis statement is that the population value is equal to the value given in the claim:

  $H_0:\mu <50$

The claim is either the null hypothesis or the alternative hypothesis. The null hypothesis statement is that the population mean is equal to the value given in the claim. If the null hypothesis is the claim, then the alternative hypothesis statement is the opposite of the null hypothesis.

  $H_1:\mu >50$

  $\mu$ is the mean percent of purchases for which an alternative supplied offered lower prices.

(b)

To determine

To find: the condition for performing the test in part (a) are met.

Answer to Problem 68E

Large sample condition is not satisfied.

Explanation of Solution

Given:

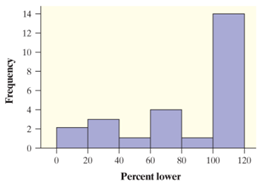
The three conditions are Random, independent (10% condition), Normal/ Large sample.

Random: Satisfied, because the sample is a random sample.

Independent: Satisfied, because sample of 25 invoices is less than 10% of the population of all invoices

Normal/ Large sample: Not satisfied, because the sample of 25 invoices is small and the distribution is skewed (as the highest bar in the histogram is to the right in the histogram).

Since the Normal/Large sample condition is not satisfied it is not suitable to perform a hypothesis test for the population mean.