Concept explainers
Videos
(a)
To Explain: the P-value.
(a)
Answer to Problem R9.7RE
There is a 0.0384
Explanation of Solution
Given:
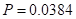
Given claim: Roulette wheel is fair and therefore the ball lends in a read slot 18 times out of 38 on average.
The claim is either the null hypothesis or the alternative hypothesis. The null hypotheses statement is that the population mean is equal to the value given in the claim. If the null hypothesis is the claim then the alternative hypothesis statement is the opposite of null hypothesis.
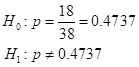
The P-value is the probability of getting the value of the test statistic or a value more extreme, when the null hypothesis is true.
There is a 0.0384 probability that get 31 successes among 50 trials or more extreme, when the roulette wheel is fair.
(b)
To Explain: the conclusion would make at the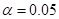 
level.
(b)
Answer to Problem R9.7RE
There is enough convincing proof that the American roulette wheel is not fair.
Explanation of Solution
Given:
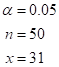
Given claim is that the proportion is 18 out of every 38
Formula used:
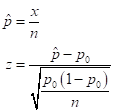
Calculation:
The claim is either the null hypothesis or the alternative hypothesis. The null hypotheses statement is that the population mean is equal to the value given in the claim. If the null hypothesis is the claim then the alternative hypothesis statement is the opposite of null hypothesis.
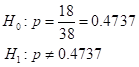
Conditions
The three conditions are: Random, independent, Normal (large counts)
Random: Satisfied, because it is safe to assume that the different spins of the wheel are random.
Independent: satisfied, the reason is that the sample of 50 spins is less than 10% of the population of all spins (assuming that there are more than 500 spins with the roulette wheel).
Normal: Satisfied, because
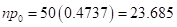and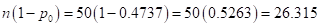 
are both at least 10.
Since all condition are satisfied, it is suitable to use a hypothesis test for the population proportion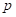
Hypothesis test
The sample proportion is
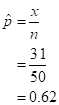
The test- statistic is
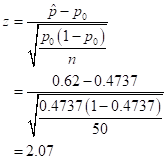
The P-value is the probability of getting the value of the test statistic, or a value more extreme, when the null hypothesis is true. Find the P-value using the normal probability table
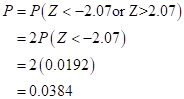
If the P-value is lesser than the significance level
then reject the null hypothesis:
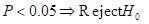
There is enough convincing proof that the American roulette wheel is not fair.
(c)
To Explain: the responses on the basis of given data.
(c)
Answer to Problem R9.7RE
Researcher is correct
Explanation of Solution
Given:
99% confidence level: (0.44, 0.80)
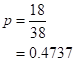
The Researcher is correct.
A 99% confidence interval associates with a significance test at the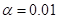 
level.
A 95% confidence interval associates with a significance test at the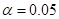 
level.
The significance test at the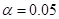 
level and therefore the associating 95% confidence interval, would lead to the opposite conclusion. Thus the there is not enough convincing evidence.
Chapter 9 Solutions
PRACTICE OF STATISTICS F/AP EXAM
Additional Math Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Algebra and Trigonometry (6th Edition)
Elementary Statistics (13th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Precalculus
Elementary Statistics: Picturing the World (7th Edition)
- 1 for all k, and set o (ii) Let X1, X2, that P(Xkb) = x > 0. Xn be independent random variables with mean 0, suppose = and Var Xk. Then, for 0x) ≤2 exp-tx+121 Στ k=1arrow_forwardLemma 1.1 Suppose that g is a non-negative, non-decreasing function such that E g(X) 0. Then, E g(|X|) P(|X|> x) ≤ g(x)arrow_forwardProof of this Theorem Theorem 1.2 (i) Suppose that P(|X| ≤ b) = 1 for some b > 0, that E X = 0, and set Var X = o². Then, for 0 0, P(X > x) ≤ e−1x+1²², P(|X|> x) ≤ 2e−x+1² 0²arrow_forward
- State and prove the Morton's inequality Theorem 1.1 (Markov's inequality) Suppose that E|X|" 0, and let x > 0. Then, E|X|" P(|X|> x) ≤ x"arrow_forward(iii) If, in addition, X1, X2, ... Xn are identically distributed, then P(S|>x) ≤2 exp{-tx+nt²o}}.arrow_forward5. State space models Consider the model T₁ = Tt−1 + €t S₁ = 0.8S-4+ Nt Y₁ = T₁ + S₁ + V₂ where (+) Y₁,..., Y. ~ WN(0,σ²), nt ~ WN(0,σ2), and (V) ~ WN(0,0). We observe data a. Write the model in the standard (matrix) form of a linear Gaussian state space model. b. Does lim+++∞ Var (St - St|n) exist? If so, what is its value? c. Does lim∞ Var(T₁ — Ît\n) exist? If so, what is its value?arrow_forward
- Let X represent the full height of a certain species of tree. Assume that X has a normal probability distribution with mean 203.8 ft and standard deviation 43.8 ft. You intend to measure a random sample of n = 211trees. The bell curve below represents the distribution of these sample means. The scale on the horizontal axis (each tick mark) is one standard error of the sampling distribution. Complete the indicated boxes, correct to two decimal places. Image attached. I filled in the yellow boxes and am not sure why they are wrong. There are 3 yellow boxes filled in with values 206.82; 209.84; 212.86.arrow_forwardCould you please answer this question using excel.Thanksarrow_forwardQuestions An insurance company's cumulative incurred claims for the last 5 accident years are given in the following table: Development Year Accident Year 0 2018 1 2 3 4 245 267 274 289 292 2019 255 276 288 294 2020 265 283 292 2021 263 278 2022 271 It can be assumed that claims are fully run off after 4 years. The premiums received for each year are: Accident Year Premium 2018 306 2019 312 2020 318 2021 326 2022 330 You do not need to make any allowance for inflation. 1. (a) Calculate the reserve at the end of 2022 using the basic chain ladder method. (b) Calculate the reserve at the end of 2022 using the Bornhuetter-Ferguson method. 2. Comment on the differences in the reserves produced by the methods in Part 1.arrow_forward
- Calculate the correlation coefficient r, letting Row 1 represent the x-values and Row 2 the y-values. Then calculate it again, letting Row 2 represent the x-values and Row 1 the y-values. What effect does switching the variables have on r? Row 1 Row 2 13 149 25 36 41 60 62 78 S 205 122 195 173 133 197 24 Calculate the correlation coefficient r, letting Row 1 represent the x-values and Row 2 the y-values. r=0.164 (Round to three decimal places as needed.) S 24arrow_forwardThe number of initial public offerings of stock issued in a 10-year period and the total proceeds of these offerings (in millions) are shown in the table. The equation of the regression line is y = 47.109x+18,628.54. Complete parts a and b. 455 679 499 496 378 68 157 58 200 17,942|29,215 43,338 30,221 67,266 67,461 22,066 11,190 30,707| 27,569 Issues, x Proceeds, 421 y (a) Find the coefficient of determination and interpret the result. (Round to three decimal places as needed.)arrow_forwardQuestions An insurance company's cumulative incurred claims for the last 5 accident years are given in the following table: Development Year Accident Year 0 2018 1 2 3 4 245 267 274 289 292 2019 255 276 288 294 2020 265 283 292 2021 263 278 2022 271 It can be assumed that claims are fully run off after 4 years. The premiums received for each year are: Accident Year Premium 2018 306 2019 312 2020 318 2021 326 2022 330 You do not need to make any allowance for inflation. 1. (a) Calculate the reserve at the end of 2022 using the basic chain ladder method. (b) Calculate the reserve at the end of 2022 using the Bornhuetter-Ferguson method. 2. Comment on the differences in the reserves produced by the methods in Part 1.arrow_forward
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman