
Determine expressions for vC(t) and iL(t) in Fig. 9.59 for the time windows (a) 0 < t <2 μs and (b) t > 2 μs.
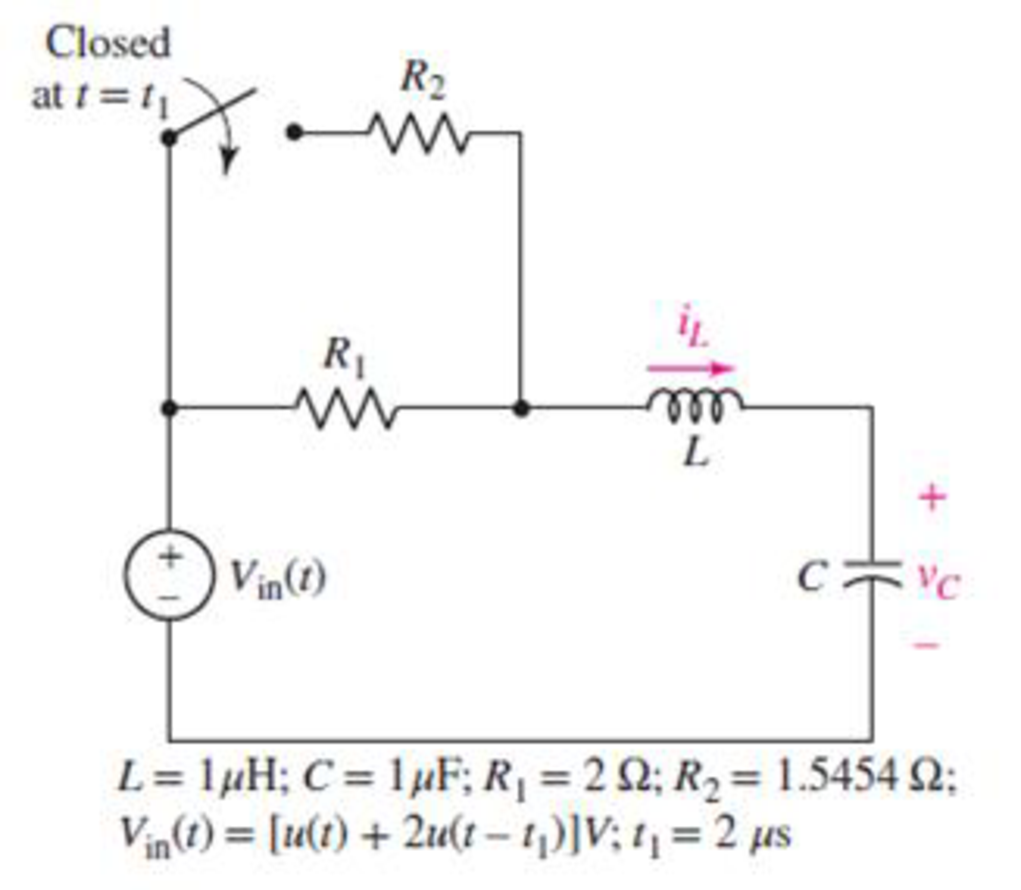
FIGURE 9.59
(a)
Determine expressions for
Answer to Problem 62E
The expressions for
Explanation of Solution
Given Data:
The range of the time is
Formula used:
The expression for the exponential damping coefficient or the neper frequency for series
Here,
The expression for the resonant frequency for series
Here,
The expression for complete natural response for source free series
Here,
The expression for the critically damped natural response of the series
Here,
Calculation:
The unit-step forcing function as a function of time which is zero for all values of its argument less than zero and which is unity for all positive values of its argument.
Here,
So, at
Since the series
The capacitor does not allow sudden change in the voltage and the inductor does not allow sudden change in the current.
So,
And,
Therefore, the voltage across the capacitor at
At
The redrawn circuit diagram is given in Figure 1 at

Refer to the redrawn Figure 1:
Substitute
Substitute
Here, the resonant frequency is equal to the exponential damping coefficient.
Therefore, the response of the circuit is critically damped.
At
Therefore, the value of forced response
Substitute
Substitute
The voltage across the capacitor at
Substitute
Rearrange for
The expression for the current flowing through
So, the current flowing through
The expression for the current flowing through the
Substitute
Rearrange for
Substitute
The current flowing through
Substitute
Substitute
Rearrange for
Substitute
The expression for the current flowing through the
Substitute
Substitute
Conclusion:
Thus, the expressions for
(b)
Determine expressions for
Answer to Problem 62E
The expressions for
Explanation of Solution
Formula used:
The expression for the damped natural frequency in series
Here,
The expression for natural response for series
Here,
Calculation:
The redrawn circuit diagram is given in Figure 2 at

Refer to the redrawn Figure 2:
The initial condition of the voltage across the
Substitute
So, the initial condition of the voltage across the
Substitute
So, the initial condition ofthe current through the
At
The expression for the equivalent resistor when resistors are connected in parallel is as follows:
Here,
So, form equation (15),
Rearrange for
The redrawn circuit diagram is given in Figure 3.
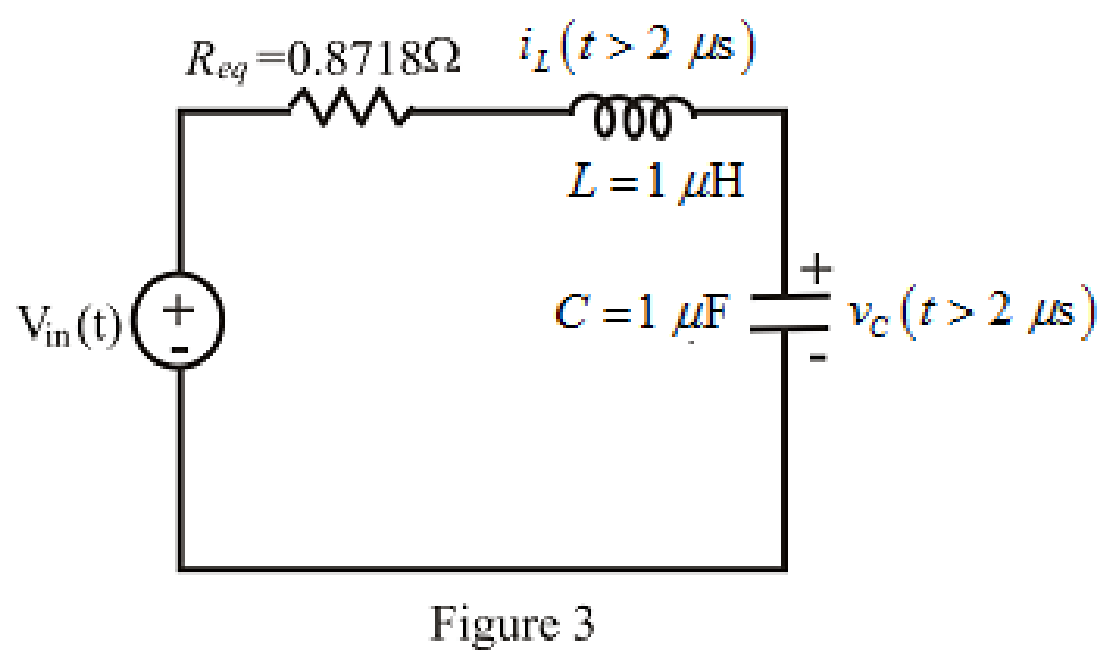
Refer to the redrawn Figure 3:
Substitute
Substitute
Here, the resonant frequency is greater than the exponential damping coefficient.
Therefore, the response of the circuit is under-damped damped.
Substitute
At
Therefore, the value of forced response
Substitute
Apply time shift in equation (18).
Substitute
The initial condition of the voltage across the
Substitute
Rearrange for
The expression for the current flowing through
So, the current flowing through
The expression for the current flowing through the
Here,
Rearrange for
Substitute
Substitute
Substitute
Substitute
Rearrange for
Substitute
Substitute
Substitute
Conclusion:
Thus, the expressions for
Want to see more full solutions like this?
Chapter 9 Solutions
ENGINEERING CIRCUIT...(LL)>CUSTOM PKG.<
- They are one quearrow_forwardO Draw the four possible negative feedback contigurations of an op-amp. Write the input and output impedances of these configurations in ideal cases. 5arrow_forwardE9.6 Determine the average power absorbed by the 4-2 and 3-2 resistors in Fig. E9.6. 302 j20 Figure E9.3 4Ω ww Figure E9.6 12/0° V j30 -j2 N 13/10° A (+60° V (OEFarrow_forward
- -160 For the P-channel JFET given in the following figure, the IDSS = 2MA a) Determine IDQ and VSDQ b) Determine the source-follower circuit transistor parameters are: Vp = +1,75 V, and λ=0. Small-signal voltage gain, Av = So VDD = 10V R₁ = 90kr Rs =5k CC1 WW R₂ = 110kn 50 C02 BL = 10 kr GNDarrow_forwardNeed a solarrow_forwardI need a drawing on how to connect the function generator, oscilliscope, and both multimeters. It is hard for me to follow text instructions. The function generator has a postive,common and negative. The oscilliscope has chanell A and B, both channels have a postive and a negative. I know you can provide text instruction but a little sketch would be very helpful thank you.arrow_forward
- Don't use ai to answer I will report you answerarrow_forwardQ1/ A three phase, 500 kVA, 6600 V, 50 Hz, 6 pole, star connected synchronous motor has synchronous impedance of J 70 ohm per phase at its normal rating, the motor is excited to give unity power factor at the input terminals. Find a) The rated current and power factor. b) The emf behind the synchronous impedance. c) The developed torque. d) The pull out torque. e) The increase in excitation which will just permit an increase of 30% of rated torque before pulling out of synchronism. (45 M.)arrow_forwardcan you fin Vds and Vgs of all transistors and specify te operating region off all transistors and prove it. 58V 5.8 V 1.8V M2 0.9V 22222 と A 4852 m 3 01 A Voy = 0.2 V V4)=0.SV λ=0.1 V-1arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





