Chapter 9, Problem 13E

Consider the circuit depicted in Fig. 9.40. (a) Obtain an expression for i_L(t) valid for all t > 0. (b) Obtain an expression for i_R(t) valid for all t > 0. (c) Determine the settling time for both i_L and i_R.

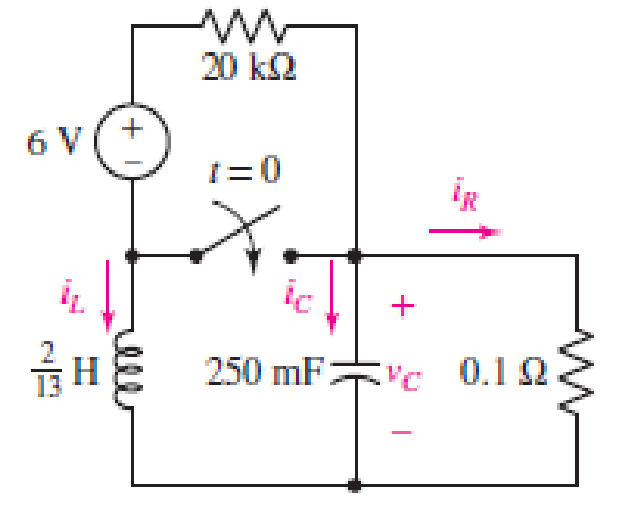
■ FIGURE 9.40

To determine

Obtain an expression for $i_L\left(t\right)$ valid for $t>0$.

Answer to Problem 13E

The current across inductor $i_L\left(t\right)$ is $-2.99\times {10}^{-4}{e}^{-0.66t}+7\times {10}^{-8}{e}^{-39.34{\text{s}}^{-1}t}\text{A}$.

Explanation of Solution

Formula used:

The expression for the exponential damping coefficient in parallel $RLC$ circuit is as follows:

$\alpha =\frac{1}{2RC}$        (1)

Here,

$\alpha$ is the exponential damping coefficient,

$R$ is the resistance of a parallel $RLC$ circuit and

$C$ is the capacitance of a parallel $RLC$ circuit.

The expression for the resonating frequency in parallel $RLC$ circuit is as follows:

${\omega }_0=\frac{1}{\sqrt{LC}}$        (2)

Here,

${\omega }_0$ is the resonating frequency and

$L$ is the inductance of a parallel $RLC$ circuit.

The expression for the two solutions of the characteristic equation of a parallel $RLC$ circuit is as follows:

$s_1=-\alpha +\sqrt{{\alpha }^2-{\omega }_0{}^2}$        (3)

$s_2=-\alpha -\sqrt{{\alpha }^2-{\omega }_0{}^2}$        (4)

Here,

$s_1$ and $s_2$ are the solutions of the characteristic equation of a parallel $RLC$ circuit.

The expression for the natural response of the parallel $RLC$ circuit is as follows:

$i_L\left(t\right)=A_1{e}^{S_{1}t}+A_2{e}^{S_{2}t}$        (5)

Here,

$i_L\left(t\right)$ is the natural response of the parallel $RLC$ circuit,

$A_1$ and $A_2$ are arbitrary constant and

$t$ is the time.

Calculation:

The redrawn circuit is shown in Figure 1 as follows:

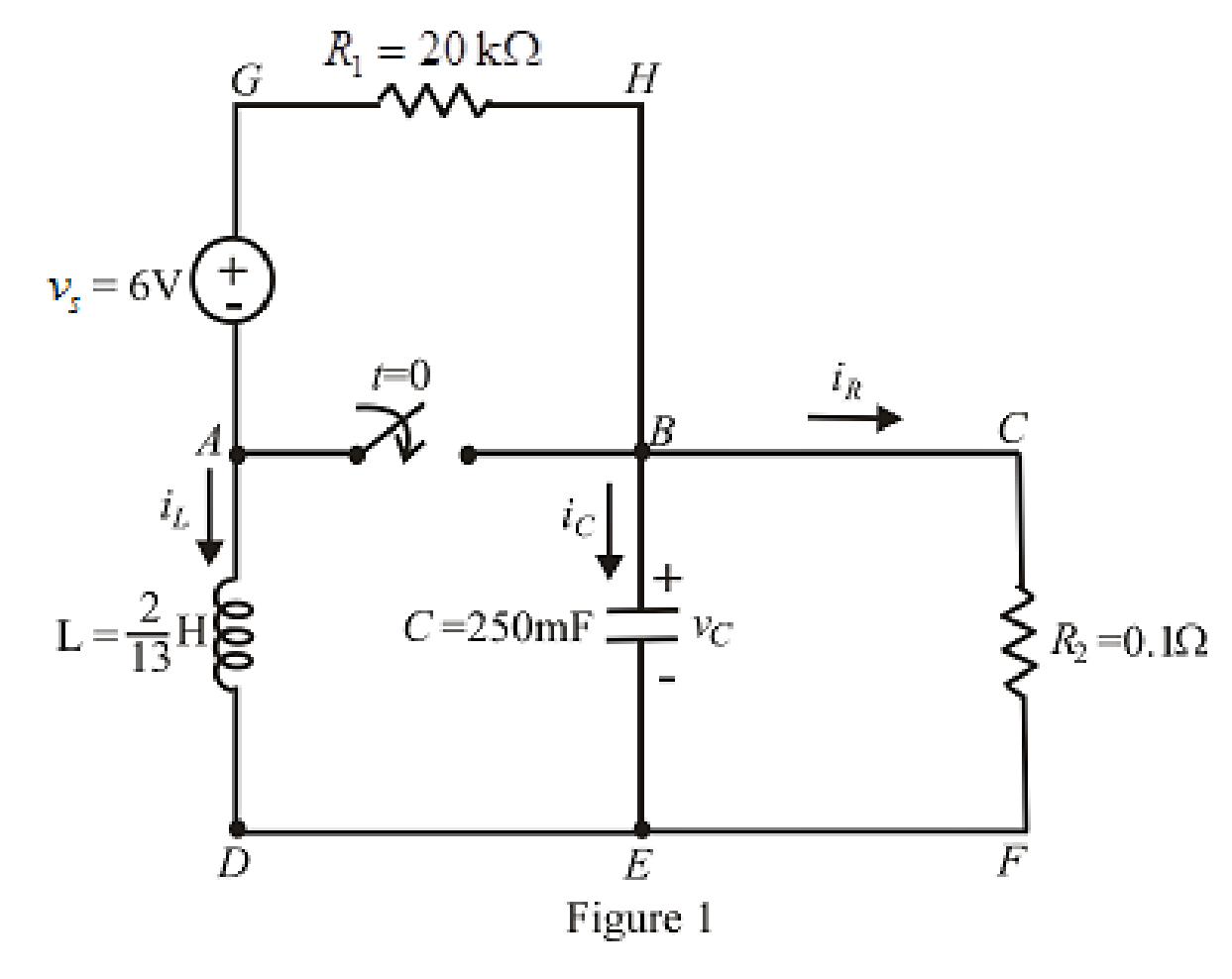
Refer to the Figure 1:

At $t=0^{-}\text{s}$ when the switch is opened the capacitor is open circuited and inductor gets short circuited because steady state is reached. The expression for current $i_L\left(0^{-}\right)$ is as follows:

$i_L\left(0^{-}\right)=-\frac{v_s}{R_1+R_2}$        (6)

Here,

$i_L\left(0^{-}\right)$ is inductor current for $t=0^{-}\text{s}$ across branch $AD$,

$v_s$ is the voltage supply from branch $GA$ and

$R_1$ and $R_2$ are the resistances across branch $GH$ and $CF$ in the circuit.

The redrawn circuit at $t=0^{-}\text{s}$ is shown in Figure 2 as follows:

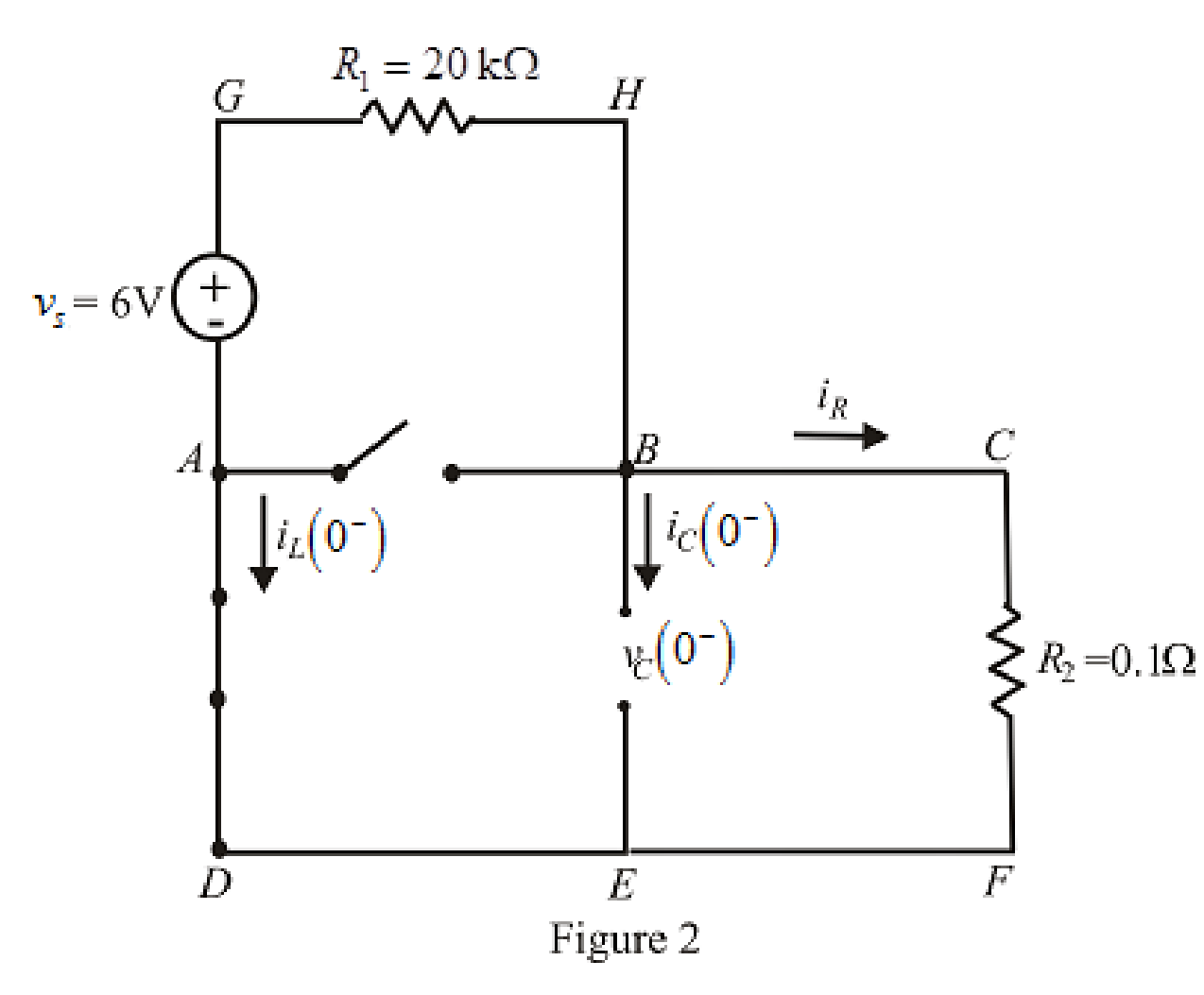
Refer to the Figure 2:

Substitute $6\text{V}$ for $v_1$, $20\text{kΩ}$ for $R_1$ and $0.1\text{Ω}$ for $R_2$ in equation (6).

$\begin{array}{c}{i}_L\left(0^{-}\right)=-\frac{6\text{V}}{20\text{kΩ}+0.1\text{Ω}}\\ =-\frac{6\text{V}}{20\times {10}^3\text{Ω}+0.1\text{Ω}}\left\{\because 1\text{kΩ}={10}^3\text{Ω}\right\}\\ =-\frac{6\text{V}}{20000.1\text{Ω}}\\ =-2.99\times {10}^{-4}\text{A}\end{array}$

The expression for voltage $v_C\left(0^{-}\right)$ is as follows:

$v_C\left(0^{-}\right)=-\left(i_L\left(0^{-}\right)\right)\left(R_2\right)$        (7)

Here,

$v_C\left(0^{-}\right)$ is the capacitor voltage across branch $BE$,

$i_L\left(0^{-}\right)$ is inductor current for $t<0$ and

$R_2$ is the resistance in the circuit.

Substitute $-2.99\times {10}^{-4}\text{A}$ for $i_L\left(0^{-}\right)$ and $0.1\text{Ω}$ for $R_2$ in equation (7).

$\begin{array}{c}{v}_C\left(0^{-}\right)=-\left(-2.99\times {10}^{-4}\text{A}\right)\left(0.1\text{Ω}\right)\\ =2.99\times {10}^{-5}\text{V}\end{array}$

Substitute $0\text{s}$ for $t$ and $-2.99\times {10}^{-4}\text{A}$ for $i_L\left(0^{-}\right)$ in equation (5).

$\begin{array}{l}-2.99\times {10}^{-4}\text{A}=A_1{e}^{S_1\times 0\text{s}}+A_2{e}^{S_2\times 0\text{s}}\\ -2.99\times {10}^{-4}=A_1+A_2\end{array}$

Rearrange for $A_1$.

$-2.99\times {10}^{-4}-A_2=A_1$        (8)

At $t=0^{+}\text{s}$ when the switch is closed the voltage of capacitor remains same as $v_C\left(0^{-}\right)$ because of small change in time. Therefore, the voltage across capacitor is,

$v_C\left(0^{-}\right)=v_C\left(0^{+}\right)$        (9)

The voltage across inductor is same as voltage across capacitor due to parallel circuit and thus, the expression for voltage across inductor is:

$v_C\left(0^{+}\right)=v_L\left(0^{+}\right)$        (10)

The redrawn circuit is shown in Figure 3 as follows:

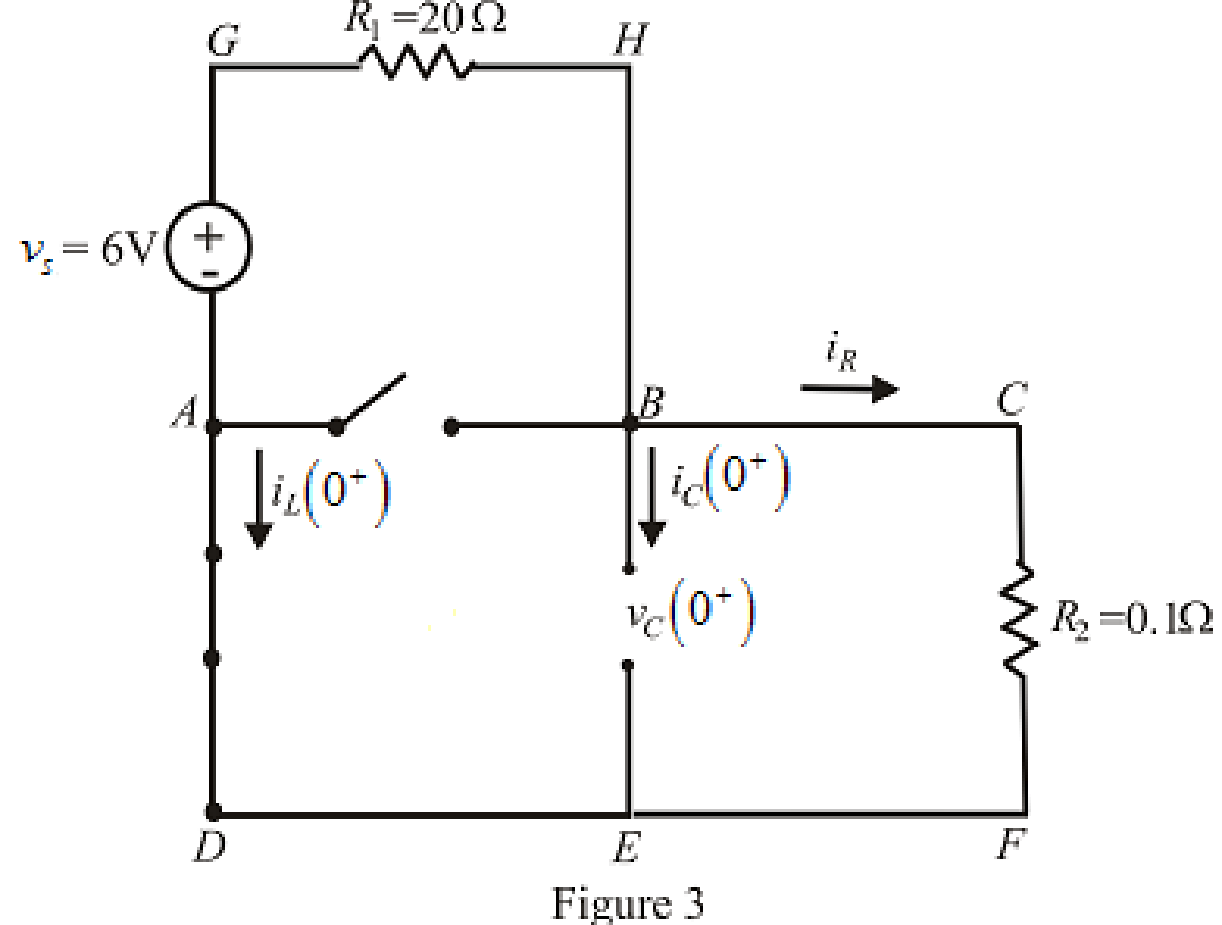
Refer to the Figure 3:

Substitute $2.99\times {10}^{-5}\text{V}$ for $v_C\left(0^{-}\right)$ in equation (9).

$2.99\times {10}^{-5}\text{V}=v_C\left(0^{+}\right)$

Substitute $2.99\times {10}^{-5}\text{V}$ for $v_C\left(0^{+}\right)$ in equation (10).

$\begin{array}{l}2.99\times {10}^{-5}\text{V}=v_L\left(0^{+}\right)\\ v_L\left(0^{+}\right)=2.99\times {10}^{-5}\text{V}\end{array}$

Differentiate equation (5) both the sides with respect to time $t$.

$\frac{d{i}_L}{dt}=A_1{s}_1{e}^{s_{1}t}+A_2{s}_2{e}^{s_{2}t}$        (11)

The expression for the voltage across inductor at time $t=0^{+}$ is:

$v_L\left(0^{+}\right)=L\frac{d{i}_L\left(0^{+}\right)}{dt}$        (12)

At $t=0^{+}\text{s}$:

Substitute $\frac{2}{13}\text{H}$ for $L$ and $2.99\times {10}^{-5}\text{V}$ for $v_L\left(0^{+}\right)$ in equation (12).

$2.99\times {10}^{-5}\text{V}=\frac{2}{13}\text{H}\times \frac{d{i}_L\left(0^{+}\right)}{dt}$

Rearrange for $\frac{d{i}_L\left(0^{+}\right)}{dt}$.

$\frac{d{i}_L\left(0^{+}\right)}{dt}=\frac{2.99\times {10}^{-5}\text{V}}{\frac{2}{13}\text{H}}$

$\frac{d{i}_L\left(0^{+}\right)}{dt}=19.43\times {10}^{-5}$        (13)

Substitute $19.43\times {10}^{-5}\text{V}$ for $\frac{d{i}_L\left(0^{+}\right)}{dt}$ and $0\text{s}$ for $t$ in equation (11).

$19.43\times {10}^{-5}=A_1{s}_1{e}^{s_1\times 0\text{s}}+A_2{s}_2{e}^{s_2\times 0\text{s}}$

$19.43\times {10}^{-5}=A_1{s}_1+A_2{s}_2$        (14)

At $t=0\text{s}$ when switch is connected then resistor $R_1$ and voltage $v_1$ gets short circuited as both elements are connected in parallel to short circuited branch.

The circuit diagram is redrawn as shown in Figure 4 for $t>0$.

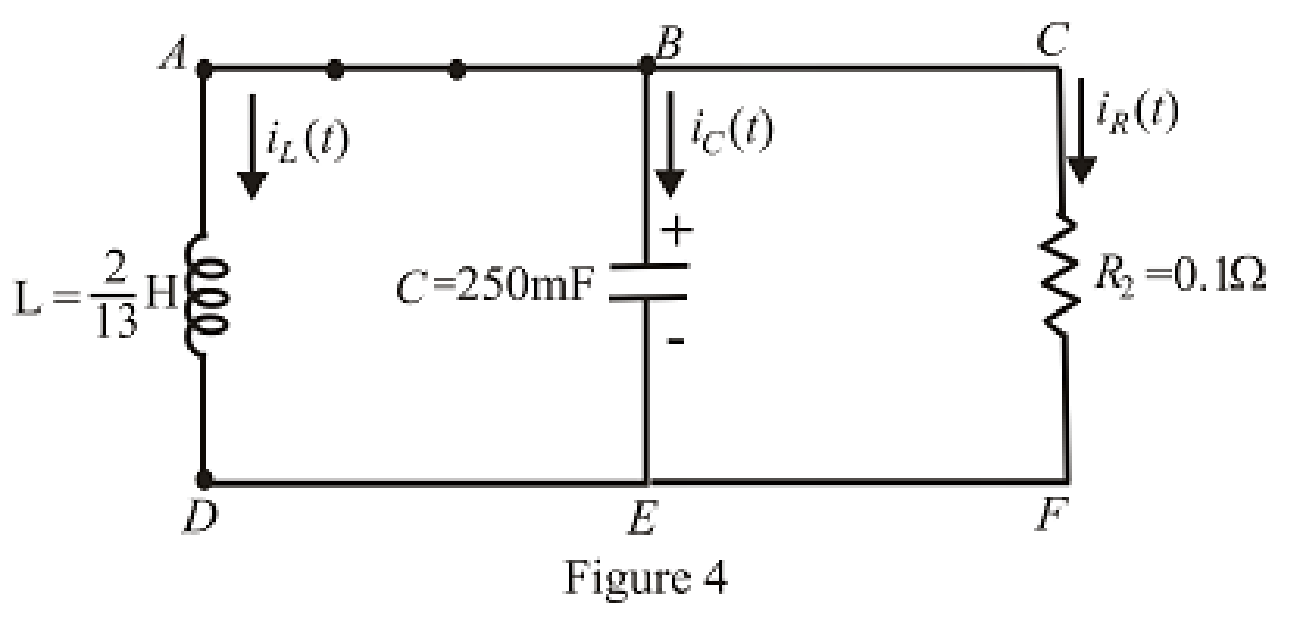
Refer to the redrawn Figure 4:

Substitute $0.1\text{ Ω}$ for $R$ and $250\text{mF}$ for $C$ in equation (1).

$\begin{array}{c}\alpha =\frac{1}{2\left(0.1\text{ Ω}\right)\left(250\text{mF}\right)}\\ =\frac{1}{2\left(0.1\text{ Ω}\right)\left(250\times {10}^{-3}\text{F}\right)}\left\{\because 1\text{mF}={10}^{-3}\text{F}\right\}\\ =\frac{1}{0.05\text{s}}\\ =20{\text{s}}^{-1}\end{array}$

Substitute $\frac{2}{13}\text{H}$ for $L$ and $250\text{mF}$ for $C$ in equation (2).

$\begin{array}{c}{\omega }_0=\frac{1}{\sqrt{\left(\frac{2}{13}\text{H}\right)\left(250\text{mF}\right)}}\\ =\frac{1}{\sqrt{\left(\frac{2}{13}\text{H}\right)\left(250\times {10}^{-3}\text{F}\right)}}\left\{\because 1\text{mF}={10}^{-3}\text{F}\right\}\\ =\frac{1}{\sqrt{0.0385}}\frac{\text{rad}}{\text{s}}\\ =5.1\frac{\text{rad}}{\text{s}}\end{array}$

As value of exponential frequency $\alpha$ is greater than resonating frequency ${\omega }_0$ which means circuit is over-damped

Substitute $20{\text{s}}^{-1}$ for $\alpha$ and $5.1\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (3).

$\begin{array}{c}{s}_1=-20{\text{s}}^{-1}+\sqrt{{\left(20{\text{s}}^{-1}\right)}^2-{\left(5.1\frac{\text{rad}}{\text{s}}\right)}^2}\\ =-20{\text{s}}^{-1}+\sqrt{400{\text{s}}^{-2}-26.01{\left(\frac{\text{rad}}{\text{s}}\right)}^2}\\ =-20{\text{s}}^{-1}+19.34{\text{s}}^{-1}\\ =-0.66{\text{s}}^{-1}\end{array}$

Substitute $20{\text{s}}^{-1}$ for $\alpha$ and $5.1\frac{\text{rad}}{\text{s}}$ for ${\omega }_0$ in equation (4).

$\begin{array}{c}{s}_2=-20{\text{s}}^{-1}-\sqrt{{\left(20{\text{s}}^{-1}\right)}^2-{\left(5.1\frac{\text{rad}}{\text{s}}\right)}^2}\\ =-20{\text{s}}^{-1}-\sqrt{400{\text{s}}^{-2}-26.01{\left(\frac{\text{rad}}{\text{s}}\right)}^2}\\ =-20{\text{s}}^{-1}-19.34{\text{s}}^{-1}\\ =-39.34{\text{s}}^{-1}\end{array}$

Substitute $-0.66{\text{s}}^{-1}$ for $s_1$ and $-39.34{\text{s}}^{-1}$ for $s_2$ in equation (14).

$19.43\times {10}^{-5}=A_1\times -0.66{\text{s}}^{-1}+A_2\times -39.34{\text{s}}^{-1}$

$19.43\times {10}^{-5}=-0.66A_1-39.34A_2$        (15)

Substitute $-2.99\times {10}^{-4}-A_2$ for $A_1$ in equation (15).

$\begin{array}{l}19.43\times {10}^{-5}=-0.66\left(-2.99\times {10}^{-4}-A_2\right)-39.34A_2\\ 19.43\times {10}^{-5}=1.97\times {10}^{-4}+0.66A_2-39.34A_2\\ 19.43\times {10}^{-5}=1.97\times {10}^{-4}-38.68A_2\end{array}$

Solve for $A_2$.

$\begin{array}{c}38.68A_2=1.97\times {10}^{-4}-19.43\times {10}^{-5}\\ 38.68A_2=2.7\times {10}^{-6}\end{array}$

Rearrange for $A_2$.

$\begin{array}{c}{A}_2=\frac{2.7\times {10}^{-6}}{38.68}\\ =7\times {10}^{-8}\end{array}$

Substitute $7\times {10}^{-8}$ for $A_2$ in equation (8).

$\begin{array}{l}-2.99\times {10}^{-4}-7\times {10}^{-8}=A_1\\ -2.99\times {10}^{-4}=A_1\end{array}$

Rearrange for $A_1$.

$A_1=-2.99\times {10}^{-4}$

Substitute $-2.99\times {10}^{-4}$ for $A_1$, $7\times {10}^{-8}$ for $A_2$, $-0.66{\text{s}}^{-1}$ for $s_1$ and $-39.34{\text{s}}^{-1}$ for $s_2$ in equation (5).

$i_L\left(t\right)=-2.99\times {10}^{-4}{e}^{-0.66t}+7\times {10}^{-8}{e}^{-39.34{\text{s}}^{-1}t}\text{A}$        (16)

Conclusion:

Thus, the current across inductor $i_L\left(t\right)$ is $-2.99\times {10}^{-4}{e}^{-0.66t}+7\times {10}^{-8}{e}^{-39.34{\text{s}}^{-1}t}\text{A}$.

To determine

Find the equation for current across resistor for $t>0\text{s}$.

Answer to Problem 13E

The equation of current $i_R\left(t\right)$ across resistor $R_2$ is $3.03\times {10}^{-4}{e}^{-0.66t}-4.23\times {10}^{-6}{e}^{-39.34t}$.

Explanation of Solution

Calculation:

Refer to the Figure 3:

The expression for current across resistor at $t=0^{+}\text{s}$ is:

$i_R\left(0^{+}\right)=\frac{v_R\left(0^{+}\right)}{R}$        (17)

At $t=0^{+}\text{s}$ the voltage across resistor is same as voltage across capacitor because of parallel $RLC$ circuit.

Therefore,

$v_R\left(0^{+}\right)=v_C\left(0^{+}\right)$        (18)

At $t>0\text{s}$ the voltage of capacitor and inductor is same as voltage at $t=0^{+}\text{s}$. Therefore, substitute $v_L$ for $v_R$ from equation (10) and $0.1\Omega$ for $R_2$ in the equation (17).

$i_R\left(t\right)=\frac{v_L\left(t\right)}{R_2}$        (19)

Substitute $L\frac{d{i}_L\left(t\right)}{dt}$ for $v_L\left(t\right)$ in equation (19).

$i_R\left(t\right)=\frac{L}{R_2}\frac{d{i}_L\left(t\right)}{dt}$        (20)

At $t>0\text{s}$,

Substitute $1.97\times {10}^{-4}{e}^{-0.66t}-2.75\times {10}^{-6}{e}^{-39.34t}$ for $\frac{d{i}_L\left(t\right)}{dt}$, $\frac{2}{13}\text{H}$ for $L$ and $0.1\Omega$ for $R_2$ in equation (20).

$\begin{array}{c}{i}_R\left(t\right)=\frac{\frac{2}{13}\text{H}}{0.1\Omega }\times \left(1.97\times {10}^{-4}{e}^{-0.66t}-2.75\times {10}^{-6}{e}^{-39.34t}\right)\text{A}/\text{s}\\ =\frac{20\text{V-s}/\text{A}}{13\Omega }\times \left(1.97\times {10}^{-4}{e}^{-0.66t}-2.75\times {10}^{-6}{e}^{-39.34t}\right)\text{A}/\text{s}\\ =1.538\times \left(1.97\times {10}^{-4}{e}^{-0.66t}-2.75\times {10}^{-6}{e}^{-39.34t}\right)\text{A}\end{array}$

$i_R\left(t\right)=3.03\times {10}^{-4}{e}^{-0.66t}-4.23\times {10}^{-6}{e}^{-39.34t}\text{A}$        (21)

Conclusion:

Thus, the equation of current $i_R\left(t\right)$ across resistor $R_2$ is

$3.03\times {10}^{-4}{e}^{-0.66t}-4.23\times {10}^{-6}{e}^{-39.34t}$.

To determine

Find the settling time for both $i_L\left(t\right)$ and $i_R\left(t\right)$.

Answer to Problem 13E

The settling time for $i_L\left(t\right)$ is $6.978\text{s}$ and for $i_R\left(t\right)$ is $7.003\text{s}$.

Explanation of Solution

Calculation:

The settling time is the time at which current reaches to $1\text{\%}$ of its maximum value.

Since the inductor current is exponential in nature and time cannot be taken as negative, therefore, inductor current takes its maximum value at $0\text{s}$, hence:

Substitute $0\text{s}$ for $t$ in equation (16).

$\begin{array}{c}{i}_L\left(0\right)=-2.99\times {10}^{-4}{e}^{-0.66{\text{s}}^{-1}\times 0\text{s}}+7\times {10}^{-8}{e}^{-39.34{\text{s}}^{-1}\times 0\text{s}}\text{A}\\ \text{=}\left(-2.99\times {10}^{-4}+7\times {10}^{-8}\right)\text{A}\end{array}$

$i_L\left(0\right)=-2.989\times {10}^{-4}\text{A}$        (22)

The maximum value of current is:

$\begin{array}{c}{i}_L{\left(t\right)}_{\max }=\left|-2.989\times {10}^{-4}\text{A}\right|\\ =2.989\times {10}^{-4}\text{A}\end{array}$

The expression for current at settling time $t_s$ is:

$i_L\left(t_s\right)=\frac{1}{100}\times i_L{\left(t\right)}_{\text{max}}$        (23)

Substitute $2.989\times {10}^{-4}\text{A}$ for $i_L{\left(t\right)}_{\text{max}}$ in equation (23),

$\begin{array}{c}{i}_L\left(t_s\right)=\frac{1}{100}\times 2.989\times {10}^{-4}\text{A}\\ =\text{2}\text{.989}\times {10}^{-6}\text{A}\end{array}$

The settling time is the time at which the current is decreased to $\text{2}\text{.989}\times {10}^{-6}\text{A}$, and is expressed as follows:

$-2.99\times {10}^{-4}{e}^{-0.66t_s}+7\times {10}^{-8}{e}^{-39.34t_s}\text{A}=\text{2}\text{.989}\times {10}^{-6}\text{A}$        (24)

Equation (24) is solved by scientific calculator which can determine the value of time $t$ at which current gets settled. The equation can be approximated for $t\ge t_s$ because the exponential function $e^{-0.66t_s}$ dominates the exponential function $e^{-39.34t}$.

$-2.99\times {10}^{-4}{e}^{-0.66t_s}\text{=}-\text{2}\text{.989}\times {10}^{-6}\text{A}$

$e^{-0.66t_s}=\frac{\text{2}\text{.989}\times {10}^{-6}\text{A}}{2.99\times {10}^{-4}}$        (25)

Take log both the side in equation (25).

$\begin{array}{l}\ln \left(e^{-0.66t_s}\right)=\text{ln}\left(\frac{\text{2}\text{.989}\times {10}^{-6}\text{A}}{2.99\times {10}^{-4}}\right)\\ -0.66t_s=-4.605\end{array}$

Rearrange for $t_s$.

$\begin{array}{c}{t}_s=\frac{4.605}{0.66}\text{s}\\ =6.978\text{s}\end{array}$

Substitute $0\text{s}$ for $t$ in equation (21).

$\begin{array}{c}{i}_R\left(0\text{s}\right)=3.03\times {10}^{-4}{e}^{-0.66\times 0\text{}\text{s}}-4.23\times {10}^{-6}{e}^{-39.34\times 0\text{s}}\text{A}\\ =3.03\times {10}^{-4}-4.23\times {10}^{-6}\text{A}\end{array}$

$i_R\left(0\text{s}\right)=2.987\times {10}^{-4}\text{A}$

The maximum value of current is:

$\begin{array}{c}{i}_R{\left(t\right)}_{\max }=\left|2.987\times {10}^{-4}\text{A}\right|\\ =2.987\times {10}^{-4}\text{A}\end{array}$

The expression for current at settling time $t_s$ is:

$i_R\left(t_s\right)=\frac{1}{100}\times i_R{\left(t\right)}_{\text{max}}$        (26)

Substitute $2.987\times {10}^{-4}\text{A}$ for $i_L{\left(t\right)}_{\text{max}}$ in equation (26).

$\begin{array}{c}{i}_R\left(t_s\right)=\frac{1}{100}\times 2.987\times {10}^{-4}\text{A}\\ =\text{2}\text{.987}\times {10}^{-6}\text{A}\end{array}$

The settling time is the time at which the current is decreased to $\text{2}\text{.987}\times {10}^{-6}\text{A}$ and is expressed as follows:

$-2.99\times {10}^{-4}{e}^{-0.66t_s}+7\times {10}^{-8}{e}^{-39.34t_s}\text{A}=\text{2}\text{.987}\times {10}^{-6}\text{A}$

The equation can be approximated for $t\ge t_s$ because the exponential function $e^{-0.66t_s}$ dominates the exponential function $e^{-39.34t}$.

$-2.99\times {10}^{-4}{e}^{-0.66t_s}\text{=2}\text{.987}\times {10}^{-6}\text{A}$

$e^{-0.66t_s}=\frac{\text{2}\text{.987}\times {10}^{-6}\text{A}}{2.99\times {10}^{-4}}$

Take log both the sides of equation (28).

$\begin{array}{l}\ln \left(e^{-0.66t_s}\right)=\text{ln}\left(\frac{\text{2}\text{.987}\times {10}^{-6}\text{A}}{2.99\times {10}^{-4}}\right)\\ -0.66t_s=-4.606\end{array}$

Rearrange for $t_s$.

$\begin{array}{c}{t}_s=\frac{4.606}{0.66}\text{s}\\ =7.003\text{s}\end{array}$

Conclusion:

Thus, the settling time for $i_L\left(t\right)$ is $6.978\text{s}$ and for $i_R\left(t\right)$ is $7.003\text{s}$.