Chapter 8.7, Problem 3E

Interpretation Introduction

Interpretation:

For anoverdamped system forced by a square wave given by $\dot{\text{x}}\text{ + x = F}\left(\text{t}\right)\text{, F}\left(\text{t}\right)\text{ =}\{\begin{array}{l}\text{+A 0 < t < T/2}\\ \text{-A T/2 < t < T}\end{array},$ if ${\text{x(0) = x}}_0$ then, ${\text{x(t) = e}}^{\text{-T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$ and ${\text{x}}_{\text{0}}\text{ = -A tanh(T/4)}$ are to be shown. The system has a unique periodic solution which is to be shown as well. The limits of $\text{x(t)}$ as $\text{T}\to \text{0 and T}\to \infty$ is to be interpreted as well as the Poincare map $\text{P}$ by ${\text{x}}_{\text{1}}{\text{ = P(x}}_{\text{0}}\text{)}$ that is ${\text{x}}_{\text{n+1}}{\text{ = P(x}}_{\text{n}}\text{)}$ is to be defined. Also, the graph of P is to be plotted and using a cobweb picture, and that $\text{P}$ has a globally stable fixed point is to be shown.

Concept Introduction:

Poincare map is defined by ${\text{x}}_{\text{k+1}}\text{ = P}\left({\text{x}}_{\text{k}}\right)$.

Answer to Problem 3E

Solution:

a) ${\text{x(t) = e}}^{\text{-T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$ is shown below.

b) ${\text{x}}_{\text{0}}\text{ = -A tanh(T/4)}$ is shown below.

c) The limits of $\text{x(t)}$ as $\text{T}\to \text{0 and T}\to \infty$ are to be interpreted below.

d) The Poincare map $\text{P}$ by ${\text{x}}_{\text{1}}{\text{ = P(x}}_{\text{0}}\text{)}$, that is, ${\text{x}}_{\text{n+1}}{\text{ = P(x}}_{\text{n}}\text{)}$ is defined below. The graph of P is to be plotted below.

e) Using a cobweb picture, $\text{P}$ has a globally stable fixed point as shown below.

Explanation of Solution

a)

The given system equations are

$\dot{\text{x}}\text{ + x = F}\left(\text{t}\right)$

Multiply the complete equation by ${\text{e}}^{\text{t}}.$

${\text{e}}^{\text{t}}{\dot{\text{x}}\text{ + e}}^{\text{t}}{\text{x = e}}^{\text{t}}\text{F}\left(\text{t}\right)$

$\frac{\text{d}}{\text{dt}}\left({\text{e}}^{\text{t}}\text{x}\right){\text{ = e}}^{\text{t}}\text{F}\left(\text{t}\right)$

Integrate it with respect to $\text{t}$ over the period $\text{T}$.

${\displaystyle \underset{\text{0}}{\overset{\text{T}}{\int }}\frac{\text{d}}{\text{dt}}\left({\text{e}}^{\text{t}}\text{x}\right)\text{dt =}{\displaystyle \underset{\text{0}}{\overset{\text{T}}{\int }}{\text{e}}^{\text{t}}\text{F}\left(\text{t}\right)\text{dt}}}$

But, $\text{F}\left(\text{t}\right)\text{ =}\{\begin{array}{l}\text{+A 0 < t < T/2}\\ \text{-A T/2 < t < T}\end{array}.$ Hence, the above equation becomes

${\left[{\text{e}}^{\text{t}}\text{x}\right]}_{\text{0}}^{\text{T}}\text{ = }{\displaystyle \underset{\text{0}}{\overset{\frac{\text{T}}{\text{2}}}{\int }}{\text{e}}^{\text{t}}}\left(\text{+A}\right)\text{dt + }{\displaystyle \underset{\frac{\text{T}}{\text{2}}}{\overset{\text{T}}{\int }}{\text{e}}^{\text{t}}\left(\text{-A}\right)}\text{ dt }$

${\text{e}}^{\text{T}}\text{x}\left(\text{T}\right)\text{ - x}\left(\text{0}\right)\text{ = A}\left({\text{e}}^{\frac{\text{T}}{\text{2}}}\text{ - 1}\right)\text{ - A}\left({\text{e}}^{\text{T}}{\text{ - e}}^{\frac{\text{T}}{\text{2}}}\right)$

Divide the complete equation by ${\text{e}}^{\text{T}}$

$\text{x}\left(\text{T}\right){\text{ - e}}^{\text{- T}}\text{x}\left(\text{0}\right)\text{ = A}\left({\text{e}}^{\text{- }\frac{\text{T}}{\text{2}}}{\text{ - e}}^{\text{- T}}\right)\text{ - A}\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)$

Rearrange it as:

$\text{x}\left(\text{T}\right){\text{ = e}}^{\text{- T}}\text{x}\left(\text{0}\right)\text{ + A}\left({\text{e}}^{\text{- }\frac{\text{T}}{\text{2}}}{\text{ - e}}^{\text{- T}}\right)\text{ - A}\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)$

Let $\text{x}\left(0\right){\text{ = x}}_{\text{0}}$. Then,

$\text{x}\left(\text{T}\right){\text{ = e}}^{\text{- T}}{\text{x}}_{\text{0}}\text{ - A}\left({\text{e}}^{\text{- }\frac{\text{T}}{\text{2}}}{\text{ + e}}^{\text{- T}}{\text{+ 1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)$

$\text{x}\left(\text{T}\right){\text{ = e}}^{\text{-T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$

Hence, it is proved.

b)

Suppose that the system has a T-periodic solution. Then, $\text{x}\left(\text{T}\right)\text{ = x}\left(\text{0}\right)$

But ${\text{x}}_{\text{0}}{\text{ = e}}^{\text{- T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}.$ Hence,

${\text{x(T) = e}}^{\text{- T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}.$

${\text{x}}_{\text{0}}{\text{ - e}}^{\text{- T}}{\text{x}}_{\text{0}}\text{ = - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$

${\text{x}}_{\text{0}}\left({\text{1 - e}}^{\text{- T}}\right)\text{ = - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$

Rearrange it as

${\text{x}}_{\text{0}}\text{ = - A}\frac{{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}}{\left({\text{1 - e}}^{\text{- T}}\right)}\text{ = - A}\frac{{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}}{\left({\text{1 + e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}$

${\text{x}}_{\text{0}}\text{ = - A}\frac{{\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}}{{\text{1 + e}}^{\text{- }\frac{\text{T}}{\text{2}}}}\text{ = - Atanh}\left(\frac{\text{T}}{\text{4}}\right)$

Hence, it is proved.

c)

$\underset{T\to 0}{\lim }\text{x}\left(\text{T}\right)=\underset{T\to 0}{\lim }{\text{e}}^{\text{- T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$

$\underset{T\to 0}{\lim }\text{x}\left(\text{T}\right){\text{ = x}}_{\text{0}}\text{ - A}{\left(\text{1 - 1}\right)}^{\text{2}}{\text{ = x}}_{\text{0}}$

Similarly,

$\underset{T\to \infty }{\lim }\text{x}\left(\text{T}\right)=\underset{T\to \infty }{\lim }{\text{e}}^{\text{- T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$

$\underset{T\to \infty }{\lim }\text{x}\left(\text{T}\right)\text{ = }\left(\text{0}\right){\text{ x}}_{\text{0}}\text{ - A}{\left(\text{1 - 0}\right)}^{\text{2}}\text{ = A}$

These results are plausible. Since as $\text{T}\to \text{0}$, $\text{x}\left(\text{t}\right)$ has no time to move anywhere and $\text{F}\left(\text{t}\right)$ has almost no time to do anything and if $\text{x}\left(\text{0}\right){\text{ = x}}_{\text{0}}$, then $\text{x}\left(\text{T}\right)\approx {\text{x}}_{\text{0}}$ and $\text{T}\to \infty$. Since $\text{x}\left(\text{T}\right){\text{= x}}_{\text{0}}$ the solution doesn’t go anywhere.

As $\text{T}\to \infty$, $\text{F}\left(\text{t}\right)$ is not periodic and the system equation becomes:

$\dot{\text{x}}\text{ + x = F}\left(\text{t}\right)\text{ = A}$

And the solution becomes

${\text{ x(t) = (x}}_{\text{0}}{\text{ - A)e}}^{\text{-t}}\text{ + A}$

d)

Since, $\text{x}\left(\text{T}\right){\text{ = e}}^{\text{-T}}{\text{x}}_{\text{0}}\text{ - A}{\left({\text{1 - e}}^{\text{- }\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$, the Poincare of the given system is

${\text{x}}_1{\text{ = P(x}}_0{\text{) = e}}^{\text{-T}}{\text{x}}_0\text{ - A}{\left({\text{1 - e}}^{\text{-}\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$

In a general form, it can be written as

${\text{x}}_{n+1}{\text{ = P(x}}_n{\text{) = e}}^{\text{-T}}{\text{x}}_n\text{ - A}{\left({\text{1 - e}}^{\text{-}\frac{\text{T}}{\text{2}}}\right)}^{\text{2}}$

It is a straight line equation of the form $\text{y = mx + b}\text{.}$ Where ${\text{slope(m) = e}}^{\text{-T}}$

The plot of $\text{P}$ at $\text{A=3, T=2}$ is

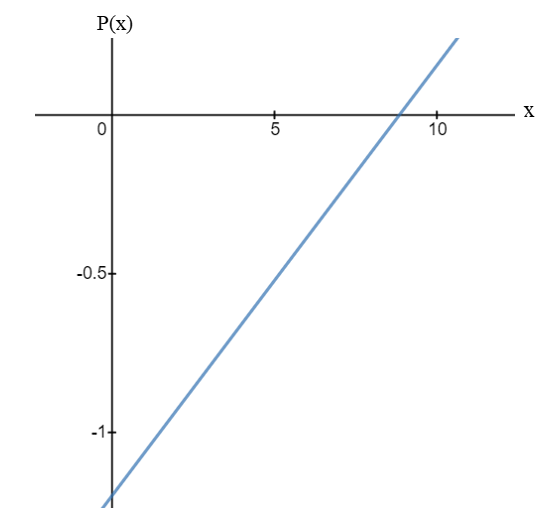
e)

The cobweb plot of the given system at $\text{A=3, T=2}$ is

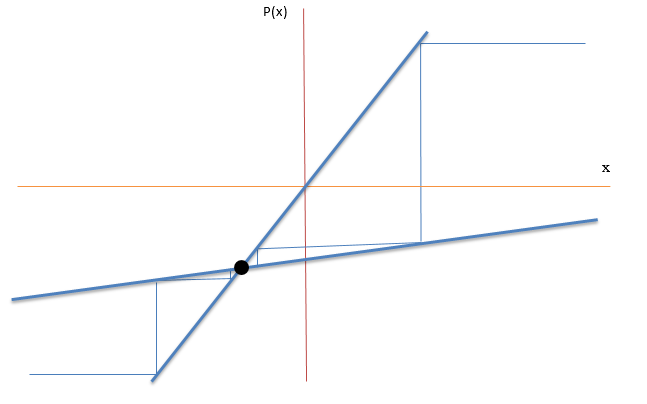
Since $\text{T > 0}$ and ${\text{m = e}}^{\text{- T}}$, then $\text{0 < m < 1}$. This ensures that $\text{P}$ has a globally stable fixed point.