
Concept explainers
Interpretation:
The pH values after the addition of each proportion of the acid to the base is to be determined. Also, the titration curve needs to be drawn.
Concept introduction:
A strong acid or a strong base can completely dissociate into its ions when they are in an aqueous solution. Pyridine is a weak base while hydrochloric acid is a strong acid. When these two chemical species are reacted with each other, they form their ionic forms and an equilibrium state.
Explanation of Solution
Initial pH of the analyte solution; Pyridine is a weak base that forms equilibrium when dissolved in water. The equilibrium is as follows.
The molarity of pyridine is 0.1 M thus, the ICE table can be created as follows:
| Reaction | Pyridine base | Pyridine ion | OH- |
| Initial | 0.1 | 0 | 0 |
| Change | -x | +x | +x |
| Equilibrium | (0.1-x) | x | x |
Here,
Thus,
The pH of the solution will be:
Addition of
Total amount of base to be neutralized
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0 | 0 |
| Change | -0.0004 | -0.0004 | 0.0004 |
| Equilibrium | 0.0021 | 0 | 0.0004 |
In the Henderson-Hasselbalch equation, the pKa is used. Therefore, the pKa for pyridine need to be calculated using its Kb.
Applying the Henderson-Hasselbalch equation,
Addition of
Total amount of pyridine to be neutralized
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0 | 0 |
| Change | -0.0008 | -0.0008 | 0.0008 |
| Equilibrium | 0.0017 | 0 | 0.0008 |
Applying the Henderson-Hasselbalch equation,
Addition of
Total amount of pyridine to be neutralized
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0 | 0 |
| Change | -0.00125 | -0.00125 | 0.00125 |
| Equilibrium | 0.00125 | 0 | 0.00125 |
Applying the Henderson-Hasselbalch equation,
Addition of
Total amount of pyridine to be neutralized
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine base |
| Initial | 0.0025 | 0 | 0 |
| Change | -0.002 | -0.002 | 0.002 |
| Equilibrium | 0.0005 | 0 | 0.002 |
Applying the Henderson-Hasselbalch equation,
Addition of
Total amount of pyridine to be neutralized
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0 | 0 |
| Change | -0.0024 | -0.0024 | +0.0024 |
| Equilibrium | 0.0001 | 0 | 0.0024 |
Applying the Henderson-Hasselbalch equation,
Addition of
Total amount of pyridine to be neutralized
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0 | 0 |
| Change | -0.0025 | -0.0025 | +0.0025 |
| Equilibrium | 0.0000 | 0 | 0.0025 |
Concentration of base after addition of base
Concentration of conjugate ion
At this point, there is no excess acid or base. Therefore, the only possible reaction here is the dissociation of the conjugate acid of the pyridine base.
Thereafter, using the Ka value for pyridine, the amount of hydrogen ions in the solution can be determined to get the pH value at this point.
| Reaction | Pyridine base | Pyridine ion | H+ |
| Initial | 0.05 | 0 | 0 |
| Change | X | x | x |
| Equilibrium | (0.05-x) | x | x |
Then the pH can be calculated as follows:
The value of x can be neglected from denominator as the acid dissociation constant has very small value.
Thus,
Addition of 26.0 mL of the acid:
Total amount of pyridine to be neutralized
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0.0026 | 0 |
| Change | -0.0025 | -0.0025 | +0.0025 |
| Equilibrium | 0.0000 | 0.0001 | 0.0025 |
The pH of the solution only depends on the concentration of HCl thus,
The pH of the solution will be:
Addition of
Amount of acid added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0.0028 | 0 |
| Change | -0.0025 | -0.0025 | +0.0025 |
| Equilibrium | 0 | 0.0003 | 0.0025 |
Here, the pH will only depend on the concentration of hydrogen ion.
Concentration of hydrogen ion
Addition of
Amount of ammonium added
Then the ICE table after the addition of base is created in order to determine the pH of the solution using Henderson-Hasselbalch equation.
| Reaction | Pyridine base | H+ | Pyridine ion |
| Initial | 0.0025 | 0.0003 | 0 |
| Change | -0.0025 | -0.0025 | +0.0025 |
| Equilibrium | 0 | 0.0005 | 0.0025 |
The pH will only depend on the concentration of hydrogen ion.
Concentration of hydrogen ion
Thus,
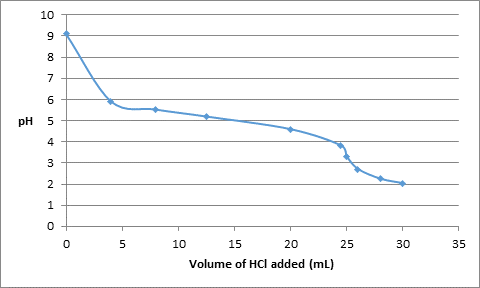
Thus, the data obtained from the calculations is as follows:
| Volume of HCl added (mL) | pH |
| 0 | 9.11 |
| 4.0 | 5.92 |
| 8.0 | 5.53 |
| 12.5 | 5.2 |
| 20.0 | 4.6 |
| 24.5 | 3.82 |
| 25.0 | 3.3 |
| 26.0 | 2.71 |
| 28.0 | 2.25 |
| 30.0 | 2.04 |
The titration curve can be represented as follows:
Want to see more full solutions like this?
Chapter 8 Solutions
EBK CHEMICAL PRINCIPLES
- For a silver-silver chloride electrode, the following potentials are observed: E°cell = 0.222 V and E(saturated KCl) = 0.197 V Use this information to find the [Cl–] (technically it’s the activity of Cl– that’s relevant here, but we’ll just call it “concentration” for simplicity) in saturated KCl.arrow_forwardA concentration cell consists of two Sn/Sn2+ half-cells. The cell has a potential of 0.10 V at 25 °C. What is the ratio of [Sn2+] (i.e., [Sn2+left-half] / [Sn2+right-half])?arrow_forwardElectrochemical cell potentials can be used to determine equilibrium constants that would be otherwise difficult to determine because concentrations are small. What is Κ for the following balanced reaction if E˚ = +0.0218 V? 3 Zn(s) + 2 Cr3+(aq) → 3 Zn2+(aq) + Cr(s) E˚ = +0.0218 Varrow_forward
- Consider the following half-reactions: Hg2+(aq) + 2e– → Hg(l) E°red = +0.854 V Cu2+(aq) + 2e– → Cu(s)E°red = +0.337 V Ni2+(aq) + 2e– → Ni(s) E°red = -0.250 V Fe2+(aq) + 2e– → Fe(s) E°red = -0.440 V Zn2+(aq) + 2e– → Zn(s) E°red = -0.763 V What is the best oxidizing agent shown above (i.e., the substance that is most likely to be reduced)?arrow_forwardCalculate the equilibrium constant, K, for MnO2(s) + 4 H+(aq) + Zn(s) → Mn2+(aq) + 2 H2O(l) + Zn2+(aq)arrow_forwardIn the drawing area below, draw the condensed structures of formic acid and ethyl formate. You can draw the two molecules in any arrangement you like, so long as they don't touch. Click anywhere to draw the first atom of your structure. A C narrow_forward
- Write the complete common (not IUPAC) name of each molecule below. Note: if a molecule is one of a pair of enantiomers, be sure you start its name with D- or L- so we know which enantiomer it is. molecule Ο C=O common name (not the IUPAC name) H ☐ H3N CH₂OH 0- C=O H NH3 CH₂SH H3N ☐ ☐ X Garrow_forward(Part A) Provide structures of the FGI products and missing reagents (dashed box) 1 eq Na* H* H -H B1 B4 R1 H2 (gas) Lindlar's catalyst A1 Br2 MeOH H2 (gas) Lindlar's catalyst MeO. OMe C6H1402 B2 B3 A1 Product carbons' origins Draw a box around product C's that came from A1. Draw a dashed box around product C's that came from B1.arrow_forwardClassify each of the amino acids below. Note for advanced students: none of these amino acids are found in normal proteins. X CH2 H3N-CH-COOH3N-CH-COO- H3N-CH-COO CH2 CH3-C-CH3 CH2 NH3 N NH (Choose one) ▼ (Choose one) S CH2 OH (Choose one) ▼ + H3N-CH-COO¯ CH2 H3N CH COO H3N-CH-COO CH2 오오 CH CH3 CH2 + O C CH3 O= O_ (Choose one) (Choose one) ▼ (Choose one) Garrow_forward
- Another standard reference electrode is the standard calomel electrode: Hg2Cl2(s) (calomel) + 2e2 Hg() +2 Cl(aq) This electrode is usually constructed with saturated KCI to keep the Cl- concentration constant (similar to what we discussed with the Ag-AgCl electrode). Under these conditions the potential of this half-cell is 0.241 V. A measurement was taken by dipping a Cu wire and a saturated calomel electrode into a CuSO4 solution: saturated calomel electrode potentiometer copper wire CuSO4 a) Write the half reaction for the Cu electrode. b) Write the Nernst equation for the Cu electrode, which will include [Cu2+] c) If the voltage on the potentiometer reads 0.068 V, solve for [Cu²+].arrow_forward2. (Part B). Identify a sequence of FGI that prepares the Synthesis Target 2,4-dimethoxy- pentane. All carbons in the Synthesis Target must start as carbons in either ethyne, propyne or methanol. Hint: use your analysis of Product carbons' origins (Part A) to identify possible structure(s) of a precursor that can be converted to the Synthesis Target using one FGI. All carbons in the Synthesis Target must start as carbons in one of the three compounds below. H = -H H = -Me ethyne propyne Synthesis Target 2,4-dimethoxypentane MeOH methanol OMe OMe MeO. OMe C₂H₁₂O₂ Product carbons' origins Draw a box around product C's that came from A1. Draw a dashed box around product C's that came from B1.arrow_forwardDraw the skeletal ("line") structure of the smallest organic molecule that produces potassium 3-hydroxypropanoate when reacted with KOH. Click and drag to start drawing a structure. Sarrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
 General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning





