Chapter 7.6, Problem 10E

(a)

To determine

The equilibrium solutions based on the significance.

Answer to Problem 10E

The 5000 aphids are enough to support a constant ladybugs population of 200.

Explanation of Solution

Given information:

Populations of aphids and ladybugs are modelled by the equations,

  $\begin{array}{l}\frac{dA}{dt}=2A-0.01AL\\ \frac{dL}{dt}=-0.5L+0.0001AL\end{array}$

Formula used:

Solving of the equation.

Calculation:

To find the equilibrium (constant) solution is of the system, solve the following equations.

  $\begin{array}{l}2A-0.01AL=0\\ -0.5L+0.0001AL=0\end{array}$

Or

  $\begin{array}{l}A\left(2-0.01L\right)=0\\ L\left(-0.5+0.0001A\right)=0\end{array}$

One solution of this system is given as,

  $A=0,L=0$

This means that there are no aphids or ladybugs, the populations are certainly not going to increase.

The other equilibrium solution can be obtained by solve the following equations.

  $\begin{array}{l}2-0.01L=0\\ -0.5+0.0001A=0\end{array}$

Or

  $\begin{array}{l}L=\frac{2}{0.01}\\ L=200\end{array}$

And

  $\begin{array}{l}0.0001A=0.5\\ A=\frac{0.5}{0.0001}\\ A=5000\end{array}$

This means that, 5000 aphids are enough to support a constant ladybugs population of 200.

Conclusion:

The 5000 aphids are enough to support a constant ladybugs population of 200.

(b)

To determine

To find: The value of $\frac{dL}{dA}$

Answer to Problem 10E

The value is $\frac{dL}{dA}=\frac{-0.5L+0.0001AL}{2A-0.01AL}$

Explanation of Solution

Given information:

Populations of aphids and ladybugs are modelled by the equations,

  $\begin{array}{l}\frac{dA}{dt}=2A-0.01AL\\ \frac{dL}{dt}=-0.5L+0.0001AL\end{array}$

Formula used:

  $\frac{dL}{dA}=\frac{\frac{dL}{dt}}{\frac{dA}{dt}}$

Calculation:

To find an expression for $\frac{dL}{dA}$ , write this term as follows:

  $\begin{array}{l}\frac{dL}{dA}=\frac{\frac{dL}{dt}}{\frac{dA}{dt}}\\ \frac{dL}{dA}=\frac{-0.5L+0.0001AL}{2A-0.01AL}\end{array}$

Conclusion:

The value is $\frac{dL}{dA}=\frac{-0.5L+0.0001AL}{2A-0.01AL}$

(c)

To determine

To explain:when there is a common phase trajectories.

Answer to Problem 10E

The phase trajectories have the point (5000, 200) in common

Explanation of Solution

Given information:

Populations of aphids and ladybugs are modelled by the equations,

  $\begin{array}{l}\frac{dA}{dt}=2A-0.01AL\\ \frac{dL}{dt}=-0.5L+0.0001AL\end{array}$

Formula used:

  $dfielplot\left(diff\left(y\left(x\right),x\right)-\left(\frac{-0.5y\left(x\right)+0.0001xy\left(x\right)}{2x-0.01xy\left(x\right)}\right),y\left(x\right),x=\mathrm{0...15000},y\left(x\right)=\mathrm{..400},color=blue\right);$

Calculation:

To sketch the direction field for this differential equation, use Maple as follows.

Consider the dependent variable L as y and the independent variable A as x in this equation to use maple.

First install the packages,

  $with\left(plots\right);with\left(DEtools\right)$

Then use the following command to sketch the direction field.

  $dfielplot\left(diff\left(y\left(x\right),x\right)-\left(\frac{-0.5y\left(x\right)+0.0001xy\left(x\right)}{2x-0.01xy\left(x\right)}\right),y\left(x\right),x=\mathrm{0...15000},y\left(x\right)=\mathrm{..400},color=blue\right);$

  

To sketch the phase portrait, use the following commands.

  $>ODEI=\left(diff\left(y\left(x\right),x=\frac{-0.5y\left(x\right)+0.0001xy\left(x\right)}{2x-0.01xy\left(x\right)}y\left(x\right),x=\mathrm{0..15000},y=\mathrm{0..400}\right)\right)$

  $ODEI=\frac{d}{dx}y\left(x\right)=\frac{-0.5y\left(x\right)+0.0001xy\left(x\right)}{2x-0.01xy\left(x\right)},y\left(x\right),x=\mathrm{0...15000},y=\mathrm{0..400}$

  

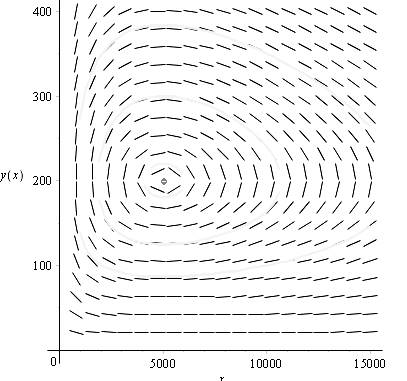
From the figure, we observe that, the phase trajectories have the point (5000, 200) in common.

Conclusion:

The phase trajectories have the point (5000, 200) in common

(d)

To determine

The phase trajectory of the aphids and ladybugs.

Answer to Problem 10E

It is not possible to describe the populations of aphids and ladybugs.

Explanation of Solution

Given information:

Populations of aphids and ladybugs are modelled by the equations,

  $\begin{array}{l}\frac{dA}{dt}=2A-0.01AL\\ \frac{dL}{dt}=-0.5L+0.0001AL\end{array}$

Formula used:

  $DEplot\left(\begin{array}{l}diff\left(y\left(x\right),x\right)=\frac{-0.5y\left(x\right)+0.0001xy\left(x\right)}{2x-0.01xy\left(x\right)},y\left(x\right),\mathrm{0..15000},\\ \left[\left[y\left(1000\right)=200\right]\left[y\left(1000\right)=400\right]\right].color=blue,arrows=LINE\end{array}\right);$

Calculation:

Use the following command, to sketch the solution curve through the point (1000, 200)

  $DEplot\left(\begin{array}{l}diff\left(y\left(x\right),x\right)=\frac{-0.5y\left(x\right)+0.0001xy\left(x\right)}{2x-0.01xy\left(x\right)},y\left(x\right),\mathrm{0..15000},\\ \left[\left[y\left(1000\right)=200\right]\left[y\left(1000\right)=400\right]\right].color=blue,arrows=LINE\end{array}\right);$

  

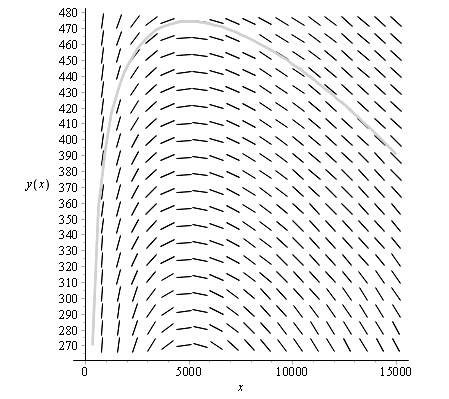
From the figure observe that, there is no solution curve exist passing through the point (1000, 200).

Hence, not possible to describe the populations of aphids and ladybugs.

Conclusion:

It is not possible to describe the populations of aphids and ladybugs.

(e)

To determine

The rough sketches of aphids and ladybugs.

Answer to Problem 10E

The rough sketches of both the populations separately cannot be drawn.

Explanation of Solution

Given information:

Populations of aphids and ladybugs are modelled by the equations,

  $\begin{array}{l}\frac{dA}{dt}=2A-0.01AL\\ \frac{dL}{dt}=-0.5L+0.0001AL\end{array}$

Formula used:

Solving of the equation.

Calculation:

From the observation of the part ((1), we cannot make rough sketches of both the populations separately.

Conclusion:

The rough sketches of both the populations separately cannot be drawn.