Chapter 7.2, Problem 12E

To determine

To sketch : the direction field for the differential equation and sketch a solution curve that passes through the point.

Explanation of Solution

Given information :

The differential equation is $y\text{'}=xy-x^2$ .

Graph :

Start by computing the slope at several points in the following table:

x	-2	-1	1	-2	-1	1	-2	-1	1
y	0	0	0	1	1	1	2	2	2
$y\text{'}=xy-x^2$	-4	-1	-1	-6	-2	0	-8	-3	1

The direction field is obtained as:

  

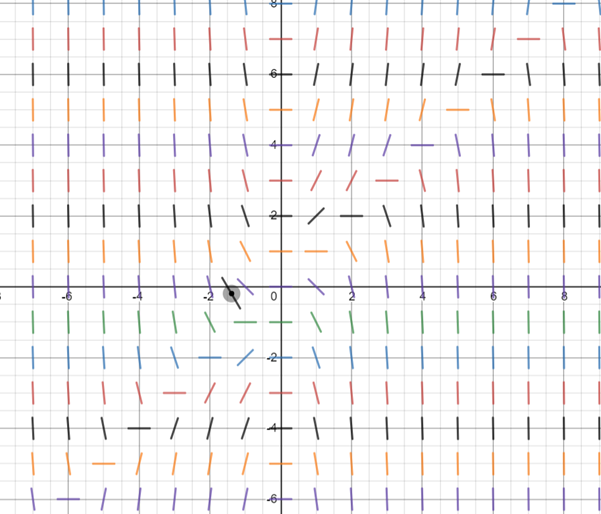
To sketch the solution curves first sketch the solution, for sketching solution start at the origin and move to the right in the direction of the line segment (which has slope 1), then continue the solution curve so that it moves parallel to the nearby line segments. And for more solution curve change the y -intercept.

Since solution graph passes through the point $\left(0,1\right)$ , so the slope intercept for that curve,

  $\begin{array}{l}y\text{'}=xy-x^2\\ y\text{'}=0·1-0\text{ [substitute }x\text{ by 0 and }y\text{ by 1]}\\ y\text{'}=0\text{ [simplify]}\end{array}$

So the graph of the solution curve intercept x - axis at $0$ ,

So the graph can be observed as:

  

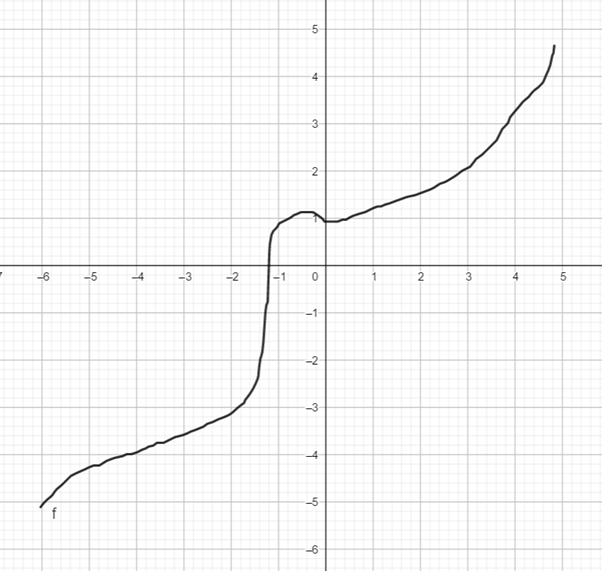
Interpretation : from the above graph it can be observed that the y -intercept change for the solution curves.