
Concept explainers
a.
To find: when the coffee cools most quickly and what happens to the rate of cooling as time goes by, explain.
a.
Answer to Problem 14E
The coffee cools the quickest in the beginning, when the temperature difference
Explanation of Solution
Given information: Suppose you have just poured a cup of freshly brewed coffee with
temperature
Formula used:
Newton’s Law of Colling states that the rate of cooling of an object is proportional to the
temperature difference and its surrounding provided that this difference is not too largeNewton’s Law of Cooling:
Calculation:
Since k and
The coffee cools the quickest in the beginning, when the temperature difference
b.
To write : a differential equation that expresses Newton’s Law of Colling for this particular situation and what is the initial condition and find this differential equation is an appropriate model for cooling.
b.
Answer to Problem 14E
Initial condition is
The rate of cooling is increases as T increases.
The temperature of coffee is maximum initially; hence rate of cooling is maximum initially.
Explanation of Solution
Given information: Newton’s Law of Colling states that the rate of cooling of an object is proportional to the temperature difference and its surrounding, provided that this difference is not too large.
Formula used:
Newton’s Law of Colling states that the rate of cooling of an object is proportional to the
temperature difference and its surrounding provided that this difference is not too largeNewton’s Law of Cooling:
Calculation:
Let the temperature of the coffee be T .
Temperature of the surroundings
So, According to Newton’s Law of Colling, the rate of cooling of coffee is:
Initial condition is
Equation of the curve is
Note the rate of cooling is increases as T increases.
The temperature of coffee is maximum initially; hence rate of cooling is maximum initially.
Also the rate of cooling decreases as T decreases, this is consistent with part (a).
c.
To make: a rough sketch of the graph of the solution of the initial- value problem in part (b).
c.
Answer to Problem 14E
Equation of the curve is
Explanation of Solution
Given information: Newton’s Law of Colling states that the rate of cooling of an object is proportional to the temperature difference and its surrounding, provided that this difference is not too large.
Calculation:
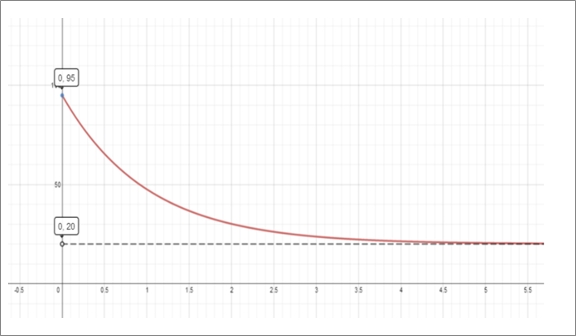
The graph is shown below.
Temperature is plotted on the vertical axis and time on the horizontal axis.
Note that the initial temperature is 95
As the time passes the temperature decreases but the rate of decrease slows down and the temperature of the coffee approaches 20
Equation of the curve is
Where k is a positive constant
Chapter 7 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
- For each graph in Figure 16, determine whether f (1) is larger or smaller than the slope of the secant line between x = 1 and x = 1 + h for h > 0. Explain your reasoningarrow_forwardPoints z1 and z2 are shown on the graph.z1 is at (4 real,6 imaginary), z2 is at (-5 real, 2 imaginary)Part A: Identify the points in standard form and find the distance between them.Part B: Give the complex conjugate of z2 and explain how to find it geometrically.Part C: Find z2 − z1 geometrically and explain your steps.arrow_forwardA polar curve is represented by the equation r1 = 7 + 4cos θ.Part A: What type of limaçon is this curve? Justify your answer using the constants in the equation.Part B: Is the curve symmetrical to the polar axis or the line θ = pi/2 Justify your answer algebraically.Part C: What are the two main differences between the graphs of r1 = 7 + 4cos θ and r2 = 4 + 4cos θ?arrow_forward
- A curve, described by x2 + y2 + 8x = 0, has a point A at (−4, 4) on the curve.Part A: What are the polar coordinates of A? Give an exact answer.Part B: What is the polar form of the equation? What type of polar curve is this?Part C: What is the directed distance when Ø = 5pi/6 Give an exact answer.arrow_forwardNew folder 10. Find the area enclosed by the loop of the curve (1- t², t-t³)arrow_forward1. Graph and find the corresponding Cartesian equation for: t X== y = t +1 2 te(-∞, ∞) 42,369 I APR 27 F5 3 MacBook Air stv A Aa T 4 DIIarrow_forward
- Middle School GP... Echo home (1) Addition and su... Google Docs Netflix Netflix New folder 9. Find the area enclosed by x = sin²t, y = cost and the y-axis.arrow_forward2. Graph and find the corresponding Cartesian equation for: (4 cos 0,9 sin 0) θ ε [0, 2π) 42,369 I APR 27 3 MacBook Air 2 tv A Aaarrow_forward30 Page< 3. Find the equation of the tangent line for x = 1+12, y = 1-3 at t = 2 42,369 APR A 27 M . tv NA 1 TAGN 2 Aa 7 MacBook Air #8arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





