PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 7.4, Problem 39E
Solution
To calculate: The minimize cost to place the order by customer.
40 operations at Refinery 1, 60 at Refinery 2, $48000, or 120 operations at Refinery 1, 20 at Refinery 2, $48000.
Given Information:
Two oil refineries produce three grades of gasoline: A, B, and C. At each refinery, the three grades of gasoline are produced in a single operation in the following proportions: Refinery 1 produces 1 unit of A, 2 units of B, and 1 unit of C; Refinery 2 produces 1 unit of A, 4 units of B, and 4 units of C. For the production of one operation, Refinery 1 charges $300 and Refinery 2 charges $600. A customer needs 100 units of A, 320 units of B. and 200 units of C.
Calculation:
Consider the given information,
Suppose that x the number of operations produced at Refinery 1 and y the number of operations produced at Refinery 2.
Write the constraints as a system of inequalities using the given information.
Write the objective function by using the given information.
Use the graphing calculator to draw the inequality and find the corner points.
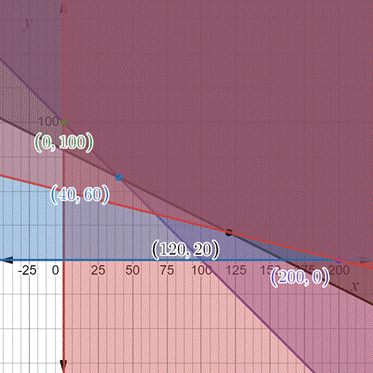
The corner points are
Now, find the value of the objective function on corner points.
Substitute 0 for x and 100 for y in the objective function.
Substitute 40 for x and 60 for y in the objective function.
Substitute 200 for x and 0 for y in the objective function.
Substitute 120 for x and 20 for y in the objective function.
The cost is minimized by producing 40 operations at Refinery 1 and 60 at Refinery 2, and by producing 120 operations at Refinery 1 and 20 at Refinery 2 and the both cost is $48000.
As the feasible region is unbounded and has
Therefore, 40 operations at Refinery 1, 60 at Refinery 2, $48000, or 120 operations at Refinery 1, 20 at Refinery 2, $48000, If conservation of operations is favoured, the first option would be the best choice..
/EXPLANATION>-->
Chapter 7 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. 7.1 - Prob. 1QRCh. 7.1 - Prob. 2QRCh. 7.1 - Prob. 3QRCh. 7.1 - Prob. 4QRCh. 7.1 - Prob. 5QRCh. 7.1 - Prob. 6QRCh. 7.1 - Prob. 7QRCh. 7.1 - Prob. 8QRCh. 7.1 - Prob. 9QRCh. 7.1 - Prob. 10QR
Ch. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10ECh. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Prob. 54ECh. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Prob. 60ECh. 7.1 - Prob. 61ECh. 7.1 - Prob. 62ECh. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.2 - Prob. 1QRCh. 7.2 - Prob. 2QRCh. 7.2 - Prob. 3QRCh. 7.2 - Prob. 4QRCh. 7.2 - Prob. 5QRCh. 7.2 - Prob. 6QRCh. 7.2 - Prob. 7QRCh. 7.2 - Prob. 8QRCh. 7.2 - Prob. 9QRCh. 7.2 - Prob. 10QRCh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Prob. 29ECh. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.2 - Prob. 63ECh. 7.2 - Prob. 64ECh. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Prob. 67ECh. 7.2 - Prob. 68ECh. 7.2 - Prob. 69ECh. 7.2 - Prob. 70ECh. 7.2 - Prob. 71ECh. 7.2 - Prob. 72ECh. 7.2 - Prob. 73ECh. 7.3 - Prob. 1QRCh. 7.3 - Prob. 2QRCh. 7.3 - Prob. 3QRCh. 7.3 - Prob. 4QRCh. 7.3 - Prob. 5QRCh. 7.3 - Prob. 6QRCh. 7.3 - Prob. 7QRCh. 7.3 - Prob. 8QRCh. 7.3 - Prob. 9QRCh. 7.3 - Prob. 10QRCh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Prob. 60ECh. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Prob. 63ECh. 7.3 - Prob. 64ECh. 7.3 - Prob. 65ECh. 7.3 - Prob. 66ECh. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - Prob. 71ECh. 7.3 - Prob. 72ECh. 7.3 - Prob. 73ECh. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.3 - Prob. 81ECh. 7.3 - Prob. 82ECh. 7.3 - Prob. 83ECh. 7.3 - Prob. 84ECh. 7.3 - Prob. 85ECh. 7.3 - Prob. 86ECh. 7.3 - Prob. 87ECh. 7.3 - Prob. 88ECh. 7.3 - Prob. 89ECh. 7.3 - Prob. 90ECh. 7.3 - Prob. 91ECh. 7.3 - Prob. 92ECh. 7.3 - Prob. 93ECh. 7.3 - Prob. 94ECh. 7.3 - Prob. 95ECh. 7.3 - Prob. 96ECh. 7.3 - Prob. 97ECh. 7.3 - Prob. 98ECh. 7.3 - Prob. 99ECh. 7.3 - Prob. 100ECh. 7.3 - Prob. 101ECh. 7.3 - Prob. 102ECh. 7.3 - Prob. 103ECh. 7.3 - Prob. 104ECh. 7.3 - Prob. 105ECh. 7.3 - Prob. 106ECh. 7.3 - Prob. 107ECh. 7.3 - Prob. 108ECh. 7.3 - Prob. 109ECh. 7.3 - Prob. 110ECh. 7.4 - Prob. 1QRCh. 7.4 - Prob. 2QRCh. 7.4 - Prob. 3QRCh. 7.4 - Prob. 4QRCh. 7.4 - Prob. 5QRCh. 7.4 - Prob. 6QRCh. 7.4 - Prob. 7QRCh. 7.4 - Prob. 8QRCh. 7.4 - Prob. 9QRCh. 7.4 - Prob. 10QRCh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7 - Prob. 1RECh. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RE
Knowledge Booster
Similar questions
- Suppose that a particle moves along a straight line with velocity v (t) = 62t, where 0 < t <3 (v(t) in meters per second, t in seconds). Find the displacement d (t) at time t and the displacement up to t = 3. d(t) ds = ["v (s) da = { The displacement up to t = 3 is d(3)- meters.arrow_forwardLet f (x) = x², a 3, and b = = 4. Answer exactly. a. Find the average value fave of f between a and b. fave b. Find a point c where f (c) = fave. Enter only one of the possible values for c. c=arrow_forwardplease do Q3arrow_forward
- Use the properties of logarithms, given that In(2) = 0.6931 and In(3) = 1.0986, to approximate the logarithm. Use a calculator to confirm your approximations. (Round your answers to four decimal places.) (a) In(0.75) (b) In(24) (c) In(18) 1 (d) In ≈ 2 72arrow_forwardFind the indefinite integral. (Remember the constant of integration.) √tan(8x) tan(8x) sec²(8x) dxarrow_forwardFind the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forward
- a -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forwardEvaluate F. dr where F(x, y, z) = (2yz cos(xyz), 2xzcos(xyz), 2xy cos(xyz)) and C is the line π 1 1 segment starting at the point (8, ' and ending at the point (3, 2 3'6arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning