Chapter 7.4, Problem 37E

Solution

To calculate: The minimum cost and how much of each ore should be processed to minimize cost.

The minimum cost is $\$1926.20$ and the amount is $13.48$ tons of ore.

Given Information:

The company extracts minerals A and B from each type of ore. It costs $50 per ton to extract 80 lb of A and 160 lb of B from ore R. It costs $60 per ton to extract 140 lb of A and 50 lb of B from ore S. Gehrke's must produce at least 4000 lb of A and 3200 lb of B.

Calculation:

Consider the given information,

Suppose that z be the amount of ore It and y be the amount of ore S , both in tons.

The objective function is the total cost. Given the rates of $50 per ton for ore It and $60 per ton for ore S . So, the objective function is defined as,

  $f=50x+60y$

First, note that the both amounts of ores must be nonnegative. So, $x>0$ and $y>0$ . At least 4000 of mineral A must be produced so $80x+140y\ge 4000$ . At least 3200 of mineral B must be produced so $160x+50y\ge 3200$ . The constraints are defined as,

  $\begin{array}{c}80x+140y\ge 4000\\ 160x+50y\ge 3200\\ x\ge 0\\ y\ge 0\end{array}$

Use the graphing calculator to draw the inequality and find the corner points.

  

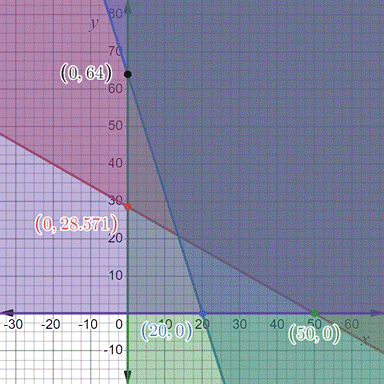
Now, take the only the solution region and corner point.

  

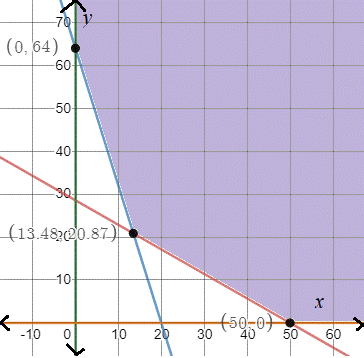
The corner points are $\left(0,64\right),\left(13.48,20.87\right),\left(50,0\right)$ .

Now, find the value of the objective function on corner points.

Substitute 0 for x and 64 for y in the objective function.

  $\begin{array}{c}f=50\left(0\right)+60\left(64\right)\\ =3840\end{array}$

Substitute $13.48$ for x and $20.87$ for y in the objective function.

  $\begin{array}{c}f=50\left(13.48\right)+60\left(20.87\right)\\ =1926.20\end{array}$

Substitute 50 for x and 0 for y in the objective function.

  $\begin{array}{c}f=50\left(50\right)+60\left(0\right)\\ =2500\end{array}$

The minimum value is $1926.20$ .

As the feasible region is unbounded and has  $x\ge 0$  and  $y\ge 0$ , and conclude that there is no maximum value for the objective function.

Therefore, the minimum cost is $\$1926.20$ and the amount is $13.48$ tons of ore.