PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 7.1, Problem 47E
Solution
a.
To calculate: The linear regression models for the populations of both cities using the given data.
The obtained matrix is
Given Information:
The table is defined,
| Time (years) | Florida (thousands) | Indiana ( thousands) |
| 1980 | 9746 | 5490 |
| 1990 | 12938 | 5544 |
| 2000 | 15982 | 6080 |
| 2010 | 18801 | 6483 |
Calculation:
Consider the given table,
| Time (years) | Florida (thousands) | Indiana ( thousands) |
| 1980 | 9746 | 5490 |
| 1990 | 12938 | 5544 |
| 2000 | 15982 | 6080 |
| 2010 | 18801 | 6483 |
Use a graphing calculator to find the linear rgeression.
Step 1. Insert the table in calculator by using the table feature and take as 0 for 1980.
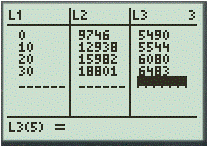
Step 2. Use the LinReg feature with first two list
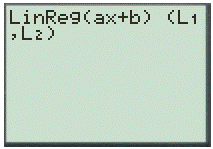
And,
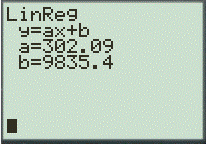
Therefore, the obtained equation is
b.
To calculate: The linear regression models for the populations of both cities using the given data.
The obtained model is
Given Information:
The table is defined as,
| Time (years) | Florida (thousands) | Indiana ( thousands) |
| 1980 | 9746 | 5490 |
| 1990 | 12938 | 5544 |
| 2000 | 15982 | 6080 |
| 2010 | 18801 | 6483 |
Calculation:
Consider the given table,
| Time (years) | Florida (thousands) | Indiana ( thousands) |
| 1980 | 9746 | 5490 |
| 1990 | 12938 | 5544 |
| 2000 | 15982 | 6080 |
| 2010 | 18801 | 6483 |
Use a graphing calculator to find the linear rgeression.
Step 1. Insert the table in calculator by using the table feature and take as 0 for 1980.
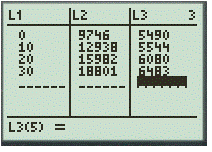
Step 2. Use the LinReg feature with first two list
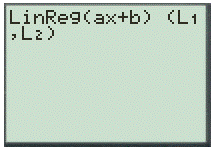
And,
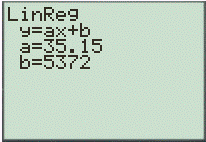
Therefore, the obtained equation is
c.
To calculate: The time when the populations of the two cities were the same as well as the common population of the two cities.
The obtained result is
Given Information:
The equations from the previous part is
Calculation:
Consider the given information,
Equate both the equations
Add the obtained value in 1980.
The corresponding year is 1963.
Now, substitute
Hence, the obtained result is
Chapter 7 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. 7.1 - Prob. 1QRCh. 7.1 - Prob. 2QRCh. 7.1 - Prob. 3QRCh. 7.1 - Prob. 4QRCh. 7.1 - Prob. 5QRCh. 7.1 - Prob. 6QRCh. 7.1 - Prob. 7QRCh. 7.1 - Prob. 8QRCh. 7.1 - Prob. 9QRCh. 7.1 - Prob. 10QR
Ch. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10ECh. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Prob. 54ECh. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Prob. 60ECh. 7.1 - Prob. 61ECh. 7.1 - Prob. 62ECh. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.2 - Prob. 1QRCh. 7.2 - Prob. 2QRCh. 7.2 - Prob. 3QRCh. 7.2 - Prob. 4QRCh. 7.2 - Prob. 5QRCh. 7.2 - Prob. 6QRCh. 7.2 - Prob. 7QRCh. 7.2 - Prob. 8QRCh. 7.2 - Prob. 9QRCh. 7.2 - Prob. 10QRCh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Prob. 29ECh. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.2 - Prob. 63ECh. 7.2 - Prob. 64ECh. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Prob. 67ECh. 7.2 - Prob. 68ECh. 7.2 - Prob. 69ECh. 7.2 - Prob. 70ECh. 7.2 - Prob. 71ECh. 7.2 - Prob. 72ECh. 7.2 - Prob. 73ECh. 7.3 - Prob. 1QRCh. 7.3 - Prob. 2QRCh. 7.3 - Prob. 3QRCh. 7.3 - Prob. 4QRCh. 7.3 - Prob. 5QRCh. 7.3 - Prob. 6QRCh. 7.3 - Prob. 7QRCh. 7.3 - Prob. 8QRCh. 7.3 - Prob. 9QRCh. 7.3 - Prob. 10QRCh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Prob. 60ECh. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Prob. 63ECh. 7.3 - Prob. 64ECh. 7.3 - Prob. 65ECh. 7.3 - Prob. 66ECh. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - Prob. 71ECh. 7.3 - Prob. 72ECh. 7.3 - Prob. 73ECh. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.3 - Prob. 81ECh. 7.3 - Prob. 82ECh. 7.3 - Prob. 83ECh. 7.3 - Prob. 84ECh. 7.3 - Prob. 85ECh. 7.3 - Prob. 86ECh. 7.3 - Prob. 87ECh. 7.3 - Prob. 88ECh. 7.3 - Prob. 89ECh. 7.3 - Prob. 90ECh. 7.3 - Prob. 91ECh. 7.3 - Prob. 92ECh. 7.3 - Prob. 93ECh. 7.3 - Prob. 94ECh. 7.3 - Prob. 95ECh. 7.3 - Prob. 96ECh. 7.3 - Prob. 97ECh. 7.3 - Prob. 98ECh. 7.3 - Prob. 99ECh. 7.3 - Prob. 100ECh. 7.3 - Prob. 101ECh. 7.3 - Prob. 102ECh. 7.3 - Prob. 103ECh. 7.3 - Prob. 104ECh. 7.3 - Prob. 105ECh. 7.3 - Prob. 106ECh. 7.3 - Prob. 107ECh. 7.3 - Prob. 108ECh. 7.3 - Prob. 109ECh. 7.3 - Prob. 110ECh. 7.4 - Prob. 1QRCh. 7.4 - Prob. 2QRCh. 7.4 - Prob. 3QRCh. 7.4 - Prob. 4QRCh. 7.4 - Prob. 5QRCh. 7.4 - Prob. 6QRCh. 7.4 - Prob. 7QRCh. 7.4 - Prob. 8QRCh. 7.4 - Prob. 9QRCh. 7.4 - Prob. 10QRCh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7 - Prob. 1RECh. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RE
Knowledge Booster
Similar questions
- Find the area between the curves. x= -2, x = 7, y=2x² +3, y=0 Set up the integral (or integrals) needed to compute this area. Use the smallest possible number of integrals. Select the correct choice below and fill in the answer boxes to complete your choice. A. 7 [[2x² +3] dx -2 B. [[ ] dx+ -2 7 S [ ] dx The area between the curves is (Simplify your answer.)arrow_forwardThe rate at which a substance grows is given by R'(x) = 105e0.3x, where x is the time (in days). What is the total accumulated growth during the first 2.5 days? Set up the definite integral that determines the accumulated growth during the first 2.5 days. 2.5 Growth = (105e0.3x) dx 0 (Type exact answers in terms of e.) Evaluate the definite integral. Growth= (Do not round until the final answer. Then round to one decimal place as needed.)arrow_forwardFind the total area of the shaded regions. y 18- 16- 14- 12- 10- 8- 6- y=ex+1-e 4- 2- 0- 2 3 4 5 -2 -4- X ☑ The total area of the shaded regions is (Type an integer or decimal rounded to three decimal places as needed.)arrow_forward
- The graph of f(x), shown here, consists of two straight line segments and two quarter circles. Find the 19 value of f(x)dx. 小 Srxdx. 19 f(x)dx y 7 -7 2 12 19 X ☑arrow_forwardCan you solve this two numerical method eqn and teach me.arrow_forwardFind the area between the following curves. x=-4, x=2, y=ex, and y = 3 - ex Set up the integral (or integrals) needed to compute this area. Use the small (Type exact answers in terms of e.) 3 In 2 A. S √ [3-2e*] dx+ -4 2 S [2ex-3] dx 3 In 2 B. dx Find the area between the curves. Area = (Type an exact answer in terms of e.)arrow_forward
- Use the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. f(x)=8-2x²: [0,4] Set up the integral (or integrals) needed to compute this area. Use the smallest possible number of integrals. Select the correct choice below and fill in the answer boxes to ○ A. dx B. 2 S 8-2x² dx+ 4 S 2 8-2x2 dx C. dx + S dx For the interval [0,4], the area between the x-axis and f(x) is (Type an integer or a simplified fraction.)arrow_forwardPollution from a factory is entering a lake. The rate of concentration of the pollutant at time t is 5 given by P'(t) = 126t², where t is the number of years since the factory started introducing pollutants into the lake. Ecologists estimate that the lake can accept a total level of pollution of 600 units before all the fish life in the lake ends. Can the factory operate for 2 years without killing all the fish in the lake? Set up the integral that would determine the pollution level after 2 years. 2 5 126t 2 dt Can the factory operate for 2 years without killing all the fish in the lake? Thee factory can operate for 2 years without killing all the fish in the lake because the value of the integral is , which is less than 600. (Round to the nearest integer as needed.)arrow_forwardUse the definite integral to find the area between the x-axis and f(x) over the indicated interval. Check first to see if the graph crosses the x-axis in the given interval. f(x)=4x-12; [2,6] The area between the x-axis and f(x) is (Type an integer or a simplified fraction.)arrow_forward
- Evaluate the definite integral. 70 √5√2-6 3 dz 70 S 5√2-6 dz= 7 江 (Type an integer or decimal rounded to two decimal places as needed.)arrow_forwardFind the area between the following curves. 2 y=x³-x²+x+4; y=5x² -7x+4 The area between the curves is (Simplify your answer.) ...arrow_forwardFind the area of the shaded region. 3- -1 -3- Q The total area of the shaded regions is (Simplify your answer.) y=9-x² Q 1 3 5 Xarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning