PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 7.3, Problem 87E
Solution
a.
To state: A linear regression equation for the population of garland if x is the number of years since 1980 and the below given table shows the population (in thousands) of two fast-growing suburbs.
| Year | Garland (thousand) | Irving (thousands) |
| 1980 | 139 | 110 |
| 1990 | 181 | 155 |
| 2000 | 216 | 192 |
| 2010 | 227 | 216 |
The resultant answer is
Given information:
The given table is:
| Year | Garland (thousand) | Irving (thousands) |
| 1980 | 139 | 110 |
| 1990 | 181 | 155 |
| 2000 | 216 | 192 |
| 2010 | 227 | 216 |
Explanation:
Consider the given table:
| Year | Garland (thousand) | Irving (thousands) |
| 1980 | 139 | 110 |
| 1990 | 181 | 155 |
| 2000 | 216 | 192 |
| 2010 | 227 | 216 |
Use a graphing calculator; enter the time (years) starting at
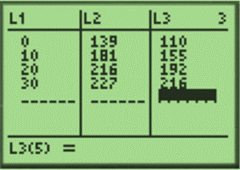
Use LinReg feature (with L1 and L2) to obtain the linear regression model for the population of Garland:
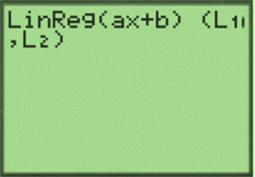
Therefore, the resultant regression equation is:
b.
To state: A linear regression equation for the population of Irving if x is the number of years since 1980 and the below given table shows the population (in thousands) of two fast-growing suburbs.
| Year | Garland (thousand) | Irving (thousands) |
| 1980 | 139 | 110 |
| 1990 | 181 | 155 |
| 2000 | 216 | 192 |
| 2010 | 227 | 216 |
The answer is
Given information:
The given table is:
| Year | Garland (thousand) | Irving (thousands) |
| 1980 | 139 | 110 |
| 1990 | 181 | 155 |
| 2000 | 216 | 192 |
| 2010 | 227 | 216 |
Explanation:
Continue from part (a), use LinReg feature (with L1 and L3) to obtain the linear regression model for the population of Irving.
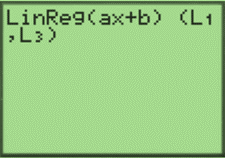
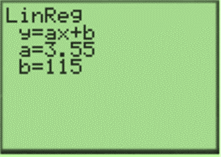
Therefore, the resultant linear regression equation is:
c.
To graph: The models from part (a) and Part (b) and use these models to determine when the population of the two cities will be about the same.
Given information:
The models from part (a) and part (b) are
Graph:
Consider the models
Now enter
And use the intersect feature to find the point of intersection:
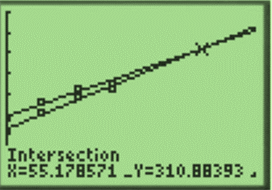
The x -coordinate of the point of intersection is about 55 which corresponds to the year
Therefore, the population of the two cities will be about the same in the year 2035.
Interpretation: Both the equations are linear equations and their intersection point is
Chapter 7 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. 7.1 - Prob. 1QRCh. 7.1 - Prob. 2QRCh. 7.1 - Prob. 3QRCh. 7.1 - Prob. 4QRCh. 7.1 - Prob. 5QRCh. 7.1 - Prob. 6QRCh. 7.1 - Prob. 7QRCh. 7.1 - Prob. 8QRCh. 7.1 - Prob. 9QRCh. 7.1 - Prob. 10QR
Ch. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10ECh. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Prob. 54ECh. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Prob. 60ECh. 7.1 - Prob. 61ECh. 7.1 - Prob. 62ECh. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.2 - Prob. 1QRCh. 7.2 - Prob. 2QRCh. 7.2 - Prob. 3QRCh. 7.2 - Prob. 4QRCh. 7.2 - Prob. 5QRCh. 7.2 - Prob. 6QRCh. 7.2 - Prob. 7QRCh. 7.2 - Prob. 8QRCh. 7.2 - Prob. 9QRCh. 7.2 - Prob. 10QRCh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Prob. 29ECh. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.2 - Prob. 63ECh. 7.2 - Prob. 64ECh. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Prob. 67ECh. 7.2 - Prob. 68ECh. 7.2 - Prob. 69ECh. 7.2 - Prob. 70ECh. 7.2 - Prob. 71ECh. 7.2 - Prob. 72ECh. 7.2 - Prob. 73ECh. 7.3 - Prob. 1QRCh. 7.3 - Prob. 2QRCh. 7.3 - Prob. 3QRCh. 7.3 - Prob. 4QRCh. 7.3 - Prob. 5QRCh. 7.3 - Prob. 6QRCh. 7.3 - Prob. 7QRCh. 7.3 - Prob. 8QRCh. 7.3 - Prob. 9QRCh. 7.3 - Prob. 10QRCh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Prob. 60ECh. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Prob. 63ECh. 7.3 - Prob. 64ECh. 7.3 - Prob. 65ECh. 7.3 - Prob. 66ECh. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - Prob. 71ECh. 7.3 - Prob. 72ECh. 7.3 - Prob. 73ECh. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.3 - Prob. 81ECh. 7.3 - Prob. 82ECh. 7.3 - Prob. 83ECh. 7.3 - Prob. 84ECh. 7.3 - Prob. 85ECh. 7.3 - Prob. 86ECh. 7.3 - Prob. 87ECh. 7.3 - Prob. 88ECh. 7.3 - Prob. 89ECh. 7.3 - Prob. 90ECh. 7.3 - Prob. 91ECh. 7.3 - Prob. 92ECh. 7.3 - Prob. 93ECh. 7.3 - Prob. 94ECh. 7.3 - Prob. 95ECh. 7.3 - Prob. 96ECh. 7.3 - Prob. 97ECh. 7.3 - Prob. 98ECh. 7.3 - Prob. 99ECh. 7.3 - Prob. 100ECh. 7.3 - Prob. 101ECh. 7.3 - Prob. 102ECh. 7.3 - Prob. 103ECh. 7.3 - Prob. 104ECh. 7.3 - Prob. 105ECh. 7.3 - Prob. 106ECh. 7.3 - Prob. 107ECh. 7.3 - Prob. 108ECh. 7.3 - Prob. 109ECh. 7.3 - Prob. 110ECh. 7.4 - Prob. 1QRCh. 7.4 - Prob. 2QRCh. 7.4 - Prob. 3QRCh. 7.4 - Prob. 4QRCh. 7.4 - Prob. 5QRCh. 7.4 - Prob. 6QRCh. 7.4 - Prob. 7QRCh. 7.4 - Prob. 8QRCh. 7.4 - Prob. 9QRCh. 7.4 - Prob. 10QRCh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7 - Prob. 1RECh. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RE
Knowledge Booster
Similar questions
- 2. Using vector algebraic operations, if - Ả = 2ây – mây – C - B = mây tây – 2, C = ây + mây + 20, D = m x + mây tậ Z Find the value(s) of m such that (a) Ả is perpendicular to B (b) B is parallel to Carrow_forward1. Determine whether the following sets are subspaces of $\mathbb{R}^3$ under the operations of addition and scalar multiplication defined on $\mathbb{R}^3$. Justify your answers.(a) $W_1=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1=3 a_2\right.$ and $\left.a_3=\mid a_2\right\}$(b) $W_2=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1=a_3+2\right\}$(c) $W_3=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: 2 a_1-7 a_2+a_3=0\right\}$(d) $W_4=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1-4 a_2-a_3=0\right\}$(e) $W_s=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: a_1+2 a_2-3 a_3=1\right\}$(f) $W_6=\left\{\left(a_1, a_2, a_3\right) \in \mathbb{R}^3: 5 a_1^2-3 a_2^2+6 a_3^2=0\right\}$arrow_forward3 Evaluate the double integral 10 y√x dy dx. First sketch the area of the integral involved, then carry out the integral in both ways, first over x and next over y, and vice versa.arrow_forward
- Question 2. i. Suppose that the random variable X takes two possible values 1 and -1, and P(X = 1) = P(X-1)=1/2. Let Y=-X. Are X and Y the same random variable? Do X and Y have the same distribution? Explain your answer. ii. Suppose that the random variable X~N(0, 1), let Y=-X. Are X and Y the same random variable? Do X and Y have the same distribution? Explain your answer.arrow_forwardProblem 4. Let f(x, y) = { Find P(X <1/2|Y = 1/2). c(x + y²) 0arrow_forwardQize f(x) x + 2x2 - 2 x² + 4x² - 4 Solve the equation using Newton Raphsonarrow_forwardSolve please thanks!arrow_forwardSolve please and thank youarrow_forwardAccording to Newton's law of universal gravitation, the force F between two bodies of constant mass GmM m and M is given by the formula F = , where G is the gravitational constant and d is the d² distance between the bodies. a. Suppose that G, m, and M are constants. Find the rate of change of force F with respect to distance d. F' (d) 2GmM b. Find the rate of change of force F with gravitational constant G = 6.67 × 10-¹¹ Nm²/kg², on two bodies 5 meters apart, each with a mass of 250 kilograms. Answer in scientific notation, rounding to 2 decimal places. -6.67x10 N/m syntax incomplete.arrow_forwardSolve please and thank youarrow_forwardmv2 The centripetal force of an object of mass m is given by F (r) = rotation and r is the distance from the center of rotation. ' where v is the speed of r a. Find the rate of change of centripetal force with respect to the distance from the center of rotation. F(r) b. Find the rate of change of centripetal force of an object with mass 500 kilograms, velocity of 13.86 m/s, and a distance from the center of rotation of 300 meters. Round to 2 decimal places. N/m (or kg/s²) F' (300)arrow_forwardSolve work shown please and thanks!arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning