Fox And Mcdonald's Introduction To Fluid Mechanics
9th Edition
ISBN: 9781118921876
Author: Pritchard, Philip J.; Leylegian, John C.; Bhaskaran, Rajesh
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7, Problem 65P
Over a certain range of air speeds, V, the lift, FL, produced by a model of a complete aircraft in a wind tunnel depends on the air speed, air density, ρ, and a characteristic length (the wing base chord length, c = 150 mm). The following experimental data is obtained for air at standard atmospheric conditions:
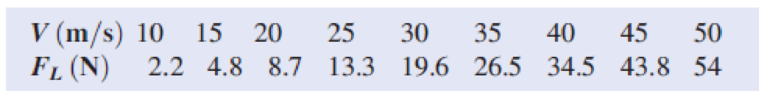
Plot the lift versus speed curve. Generate and plot data for the lift produced by the prototype, which has a wing base chord length of 5 m, over a speed range of 75 m/s to 250 m/s.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
I want a human solution
(Read Image)
47
14
16
12
34
10
12
12
33
Chapter 7 Solutions
Fox And Mcdonald's Introduction To Fluid Mechanics
Ch. 7 - The slope of the free surface of a steady wave in...Ch. 7 - One-dimensional unsteady flow in a thin liquid...Ch. 7 - In atmospheric studies the motion of the earths...Ch. 7 - Fluid fills the space between two parallel plates....Ch. 7 - By using order of magnitude analysis, the...Ch. 7 - Consider a disk of radius R rotating in an...Ch. 7 - An unsteady, two-dimensional, compressible,...Ch. 7 - Experiments show that the pressure drop for flow...Ch. 7 - At very low speeds, the drag on an object is...Ch. 7 - We saw in Chapter 3 that the buoyant force, FB, on...
Ch. 7 - Assume that the velocity acquired by a body...Ch. 7 - Derive by dimensional analysis an expression for...Ch. 7 - The speed of shallow water waves in the ocean...Ch. 7 - The speed, V, of a free-surface wave in shallow...Ch. 7 - The boundary-layer thickness, , on a smooth flat...Ch. 7 - The speed, V, of a free-surface gravity wave in...Ch. 7 - Derive an expression for the velocity of very...Ch. 7 - Derive an expression for the axial thrust exerted...Ch. 7 - Derive an expression for drag force on a smooth...Ch. 7 - The energy released during an explosion, E, is a...Ch. 7 - Measurements of the liquid height upstream from an...Ch. 7 - The load-carrying capacity, W, of a journal...Ch. 7 - Derive an expression for the drag force on a...Ch. 7 - A circular disk of diameter d and of negligible...Ch. 7 - Two cylinders are concentric, the outer one fixed...Ch. 7 - The time, t, for oil to drain out of a viscosity...Ch. 7 - You are asked to find a set of dimensionless...Ch. 7 - A continuous belt moving vertically through a bath...Ch. 7 - Derive an expression for the frictional torque...Ch. 7 - Tests on the established flow of six different...Ch. 7 - The power, P, required to drive a fan is believed...Ch. 7 - The sketch shows an air jet discharging...Ch. 7 - The diameter, d, of bubbles produced by a...Ch. 7 - Choked-flow nozzles are often used to meter the...Ch. 7 - A large tank of liquid under pressure is drained...Ch. 7 - Spin plays an important role in the flight...Ch. 7 - The power loss, P, in a journal bearing depends on...Ch. 7 - The thrust of a marine propeller is to be measured...Ch. 7 - The rate dT/dt at which the temperature T at the...Ch. 7 - When a valve is closed suddenly in a pipe with...Ch. 7 - An airship is to operate at 20 m/s in air at...Ch. 7 - An airplane wing of 3 m chord length moves through...Ch. 7 - A flat plate 1.5 m long and 0.3 m wide is towed at...Ch. 7 - This 1:12 pump model using water at 15C simulates...Ch. 7 - An ocean-going vessel is to be powered by a...Ch. 7 - On a cruise ship, passengers complain about the...Ch. 7 - A 1:3 scale model of a torpedo is tested in a wind...Ch. 7 - A flow rate of 0:18 m3/s of water at 20C...Ch. 7 - A force of 9 N is required to tow a 1:50 ship...Ch. 7 - An airplane wing, with chord length of 1.5 m and...Ch. 7 - A water pump with impeller diameter of 24 in. is...Ch. 7 - A model hydrofoil is to be tested at 1:20 scale....Ch. 7 - A ship 120 m long moves through freshwater at 15C...Ch. 7 - A 1:30 scale model of a cavitating overflow...Ch. 7 - In some speed ranges, vortices are shed from the...Ch. 7 - A 1:8 scale model of a tractor-trailer rig is...Ch. 7 - On a cruise ship, passengers complain about the...Ch. 7 - When a sphere of 0.25 mm diameter and specific...Ch. 7 - The flow about a 150 mm artillery projectile which...Ch. 7 - Your favorite professor likes mountain climbing,...Ch. 7 - A 1:50-scale model of a submarine is to be tested...Ch. 7 - Consider water flow around a circular cylinder, of...Ch. 7 - A 1:10 scale model of a tractor-trailer rig is...Ch. 7 - The power, P, required to drive a fan is assumed...Ch. 7 - Over a certain range of air speeds, V, the lift,...Ch. 7 - The pressure rise, p, of a liquid flowing steadily...Ch. 7 - An axial-flow pump is required to deliver 0.75...Ch. 7 - A model propeller 1 m in diameter is tested in a...Ch. 7 - Consider Problem 7.38. Experience shows that for...Ch. 7 - Closed-circuit wind tunnels can produce higher...Ch. 7 - A 1:16 model of a bus is tested in a wind tunnel...Ch. 7 - The propagation speed of small-amplitude surface...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
Four prospectors with only one lantern must walk through a mine shaft. At most, two prospectors can travel toge...
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
Before the uniform distributed load is applied to the beam, there is a small gap of 0.2 mm between the beam and...
Mechanics of Materials (10th Edition)
Personnel Report NOTE: This assignment assumes you have already completed Programming Challenges 4 and 5. Write...
Starting Out with C++ from Control Structures to Objects (9th Edition)
The ____________ is always transparent.
Web Development and Design Foundations with HTML5 (8th Edition)
Porter’s competitive forces model: The model is used to provide a general view about the firms, the competitors...
Management Information Systems: Managing The Digital Firm (16th Edition)
When determining whether a number is inside a range, its best to use this operator. a. b. ! c. | | d. ? :
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 3. A steam power plant has an average monthly net power delivery of 740 MW over the course of a year. This power delivery is accomplished by burning coal in the boiler. The coal has a heating value of 9150 Btu/lbm. The cost of the coal is $14.20/ton. The overall thermal efficiency of the plant is, nth = Wnet Qboiler = 0.26 = 26% Determine the annual cost of the coal required to deliver the given average monthly power.arrow_forward47 14 16 12 34 10 12 12 33arrow_forward= The forces F₁ = 590 lb, F₂ = 380 lb, F3 = 240 lb and F 330 lb. Determine the forces in each member of the truss. Use positive values to indicate tension and negative values to indicate compression. a a a D b F₁ A 000 B. 779977 F₂V H G E F4 b BY NC SA 2013 Michael Swanbom Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 6 ft b 10.1 ft The force in member AB is lb. The force in member AH is lb. The force in member GH is lb. The force in member BH is lb. The force in member BC is lb. The force in member BG is lb. The force in member EG is lb. The force in member CD is lb. The force in member DE is lb. The force in member CE is lb. The force in member CG is lb.arrow_forward
- Multiple Choice Circle the best answer to each statement. 1. Which type of surface deviation is controlled by a cy- lindricity tolerance but not by a circularity tolerance? A. B. C. Ovality Taper Lobing D. None of the above 2. When verifying a cylindricity tolerance, the inspec- tion method must be able to collect a set of points and determine the: A. Distance between two coaxial cylinders that con- tain the set of points B. Cylinder that circumscribes the set of points C. Cylinder that inscribes the set of points D. Distance between two coaxial circles that contain the set of points 3. Where Rule #1 applies to a cylindrical regular feature of size, the tolerance value of a cylindricity tolerance applied to the feature of size must be tolerance. A. Less than B. Equal to C. Greater than D. None of the above the size 4. Which of the following modifiers may be applied with a cylindricity tolerance? A. M B. C. ℗ D. Ø 5. Which geometric tolerance can provide an indirect cylindricity…arrow_forwardThe beam AB is attached to the wall in the xz plane by a fixed support at A. A force of F = (−129î + 69.0ĵ + 3591) N is applied to the end of the beam at B. The weight of the beam can be modeled with a uniform distributed load of intensity w = 85.0 N/m acting in the negative z direction along its entire length. Find the support reactions at A. Z с A b a B F y Cc 10 BY NC SA 2016 Eric Davishahl X Values for dimensions on the figure are given in the following. table. Note the figure may not be to scale. Variable Value a 5.60 m b 5.00 m C 3.70 m A II = MA = ( m 2.> ~.> + + k) N k) N-arrow_forwardneed help?arrow_forward
- A bent pipe is attached to a wall with brackets as shown. A force of F = 180 lb is applied to the end of the tube with direction indicated by the dimensions in the figure. Determine the support reactions at the brackets B, C, and D. Model these brackets as journal bearings (only force reactions perpendicular to the axis of the tube) and neglect couple moment reactions. Assume the distance between the supports at B and C and the tube bends nearby are negligible such that the support at C is directly above the support at D and the dimension g gives the distance between supports B and C. Enter your answers in Cartesian components. 2013 Michael Swanbom cc 10 BY NC SA g h א B 8° У A C x каж Values for dimensions on the figure are given in the table below. Note the figure may not be to scale. Variable Value a 6.72 in b 11.8 in с 14.8 in d 42.0 in h 26.6 in g 28.0 in → The reaction at B is B = lb. The reaction at C is C = lb. The reaction at D is D = lb. + << + + 2. + + 557 〈んarrow_forwardThe force F1 = 10 kN, F2 = 10 kN, F3 = 10 kN, F4 = 5 KN are acting on the sttructure shown. Determine the forces in the members specified below. Use positive values to indicate tension and negative values to indicate compression. F2 D b F1 F3 C E b F4 b B F a G Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 3 m b 4 m The force in member BC is KN. The force in member BE is KN. The force in member EF is KN.arrow_forwardh = The transmission tower is subjected to the forces F₁ 3.6 KN at 50° and F2 = 3.3 kN at = 35°. Determine the forces in members BC, BP, PQ, PC, CD, DP and NP. Use positive values to indicate tension and negative values to indicate compression. 不 кажаж в *а*аж E N M d d IF, c B CENTER LINE S อ K F₂ Kbb cc 10 BY NC SA 2013 Michael Swanbom Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 1.7 m b 4.9 m с 3 m d 5.2 m h 8.4 m Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 1.7 m 4.9 m с 3 m d 5.2 m h 8.4 m The force in member BC is KN. The force in member BP is KN. The force in member PQ is KN. The force in member PC is KN. The force in member CD is KN. The force in member DP is KN. The force in member NP is KN.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Unit Conversion the Easy Way (Dimensional Analysis); Author: ketzbook;https://www.youtube.com/watch?v=HRe1mire4Gc;License: Standard YouTube License, CC-BY