
Fox And Mcdonald's Introduction To Fluid Mechanics
9th Edition
ISBN: 9781118921876
Author: Pritchard, Philip J.; Leylegian, John C.; Bhaskaran, Rajesh
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 7, Problem 30P
Tests on the established flow of six different liquids in smooth pipes of various sizes yield the following data:
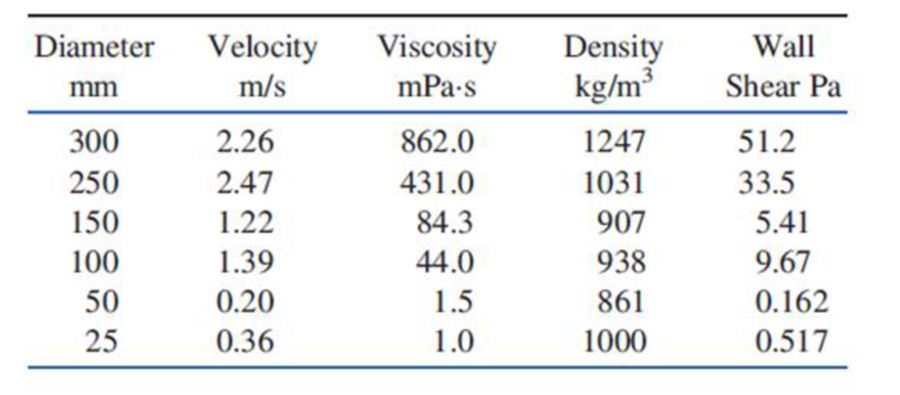
Make a dimensional analysis of this problem and a plot of the resulting dimensionless numbers as ordinate and abscissa. What conclusions may be drawn from the plot?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A liquid of density ? and viscosity ? flows by gravity through a hole of diameter d in the bottom of a tank of diameter DFig. . At the start of the experiment, the liquid surface is at height h above the bottom of the tank, as sketched. The liquid exits the tank as a jet with average velocity V straight down as also sketched. Using dimensional analysis, generate a dimensionless relationship for V as a function of the other parameters in the problem. Identify any established nondimensional parameters that appear in your result. (Hint: There are three length scales in this problem. For consistency, choose h as your length scale.) except for a different dependent parameter, namely, the time required to empty the tank tempty. Generate a dimensionless relationship for tempty as a function of the following independent parameters: hole diameter d, tank diameter D, density ? , viscosity ? , initial liquid surface height h, and gravitational acceleration g.
Problems H.pdf >
Problems H.W: Lecture No.6 Part 2
Q1-(2.4-4, Holland): A fluid of density (p) and dynamic viscosity (u) flows in s.s in a cylindrical
pipe of inside diameter (d) with mean linear velocity (u). Derive an expression for the pressure gradient
AP/L in terms of p, u, d & u. By dimensional analysis (Note Lect. No.3).
Q2-An oil with a viscosity of u= 0.40 N-s/m and density p= 900 kg/m flows in a pipe of diameter d=
0.20m.
(a) What pressure drop, pl-p2, is needed to produce a flowrate of Q=2.0x10-5 m/s if the pipe is
horizontal with xl=0 and x2=10 m?
(b) How steep a hill,
part (a), but with pl=p2? (c) For the conditions of part (b), if pl=200 kPa, what is the pressure at
section, x3=5 m, where x is measured along the pipe?
„must the pipe be on if the oil is to flow through the pipe at the same rate as in
II
I need the answer as soon as possible
Chapter 7 Solutions
Fox And Mcdonald's Introduction To Fluid Mechanics
Ch. 7 - The slope of the free surface of a steady wave in...Ch. 7 - One-dimensional unsteady flow in a thin liquid...Ch. 7 - In atmospheric studies the motion of the earths...Ch. 7 - Fluid fills the space between two parallel plates....Ch. 7 - By using order of magnitude analysis, the...Ch. 7 - Consider a disk of radius R rotating in an...Ch. 7 - An unsteady, two-dimensional, compressible,...Ch. 7 - Experiments show that the pressure drop for flow...Ch. 7 - At very low speeds, the drag on an object is...Ch. 7 - We saw in Chapter 3 that the buoyant force, FB, on...
Ch. 7 - Assume that the velocity acquired by a body...Ch. 7 - Derive by dimensional analysis an expression for...Ch. 7 - The speed of shallow water waves in the ocean...Ch. 7 - The speed, V, of a free-surface wave in shallow...Ch. 7 - The boundary-layer thickness, , on a smooth flat...Ch. 7 - The speed, V, of a free-surface gravity wave in...Ch. 7 - Derive an expression for the velocity of very...Ch. 7 - Derive an expression for the axial thrust exerted...Ch. 7 - Derive an expression for drag force on a smooth...Ch. 7 - The energy released during an explosion, E, is a...Ch. 7 - Measurements of the liquid height upstream from an...Ch. 7 - The load-carrying capacity, W, of a journal...Ch. 7 - Derive an expression for the drag force on a...Ch. 7 - A circular disk of diameter d and of negligible...Ch. 7 - Two cylinders are concentric, the outer one fixed...Ch. 7 - The time, t, for oil to drain out of a viscosity...Ch. 7 - You are asked to find a set of dimensionless...Ch. 7 - A continuous belt moving vertically through a bath...Ch. 7 - Derive an expression for the frictional torque...Ch. 7 - Tests on the established flow of six different...Ch. 7 - The power, P, required to drive a fan is believed...Ch. 7 - The sketch shows an air jet discharging...Ch. 7 - The diameter, d, of bubbles produced by a...Ch. 7 - Choked-flow nozzles are often used to meter the...Ch. 7 - A large tank of liquid under pressure is drained...Ch. 7 - Spin plays an important role in the flight...Ch. 7 - The power loss, P, in a journal bearing depends on...Ch. 7 - The thrust of a marine propeller is to be measured...Ch. 7 - The rate dT/dt at which the temperature T at the...Ch. 7 - When a valve is closed suddenly in a pipe with...Ch. 7 - An airship is to operate at 20 m/s in air at...Ch. 7 - An airplane wing of 3 m chord length moves through...Ch. 7 - A flat plate 1.5 m long and 0.3 m wide is towed at...Ch. 7 - This 1:12 pump model using water at 15C simulates...Ch. 7 - An ocean-going vessel is to be powered by a...Ch. 7 - On a cruise ship, passengers complain about the...Ch. 7 - A 1:3 scale model of a torpedo is tested in a wind...Ch. 7 - A flow rate of 0:18 m3/s of water at 20C...Ch. 7 - A force of 9 N is required to tow a 1:50 ship...Ch. 7 - An airplane wing, with chord length of 1.5 m and...Ch. 7 - A water pump with impeller diameter of 24 in. is...Ch. 7 - A model hydrofoil is to be tested at 1:20 scale....Ch. 7 - A ship 120 m long moves through freshwater at 15C...Ch. 7 - A 1:30 scale model of a cavitating overflow...Ch. 7 - In some speed ranges, vortices are shed from the...Ch. 7 - A 1:8 scale model of a tractor-trailer rig is...Ch. 7 - On a cruise ship, passengers complain about the...Ch. 7 - When a sphere of 0.25 mm diameter and specific...Ch. 7 - The flow about a 150 mm artillery projectile which...Ch. 7 - Your favorite professor likes mountain climbing,...Ch. 7 - A 1:50-scale model of a submarine is to be tested...Ch. 7 - Consider water flow around a circular cylinder, of...Ch. 7 - A 1:10 scale model of a tractor-trailer rig is...Ch. 7 - The power, P, required to drive a fan is assumed...Ch. 7 - Over a certain range of air speeds, V, the lift,...Ch. 7 - The pressure rise, p, of a liquid flowing steadily...Ch. 7 - An axial-flow pump is required to deliver 0.75...Ch. 7 - A model propeller 1 m in diameter is tested in a...Ch. 7 - Consider Problem 7.38. Experience shows that for...Ch. 7 - Closed-circuit wind tunnels can produce higher...Ch. 7 - A 1:16 model of a bus is tested in a wind tunnel...Ch. 7 - The propagation speed of small-amplitude surface...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
Object reusability has been a factor in the increased use of object-oriented programming.
Starting Out with Python (4th Edition)
Fill in the blanks in each of the following statements: A relation that has no partial functional dependencies ...
Modern Database Management
Why is the study of database technology important?
Database Concepts (8th Edition)
What is pseudocode?
Starting Out With Visual Basic (8th Edition)
Write a program that reads three whole numbers and displays the average of the three numbers.
Java: An Introduction to Problem Solving and Programming (8th Edition)
42. A container holding 1.5 moles [mol] of oxygen (formula: O2, molecular weight = 32 grams per mole [g/mol]) a...
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 5.13 The torque due to the frictional resistance of the oil film between a rotating shaft and its bearing is found to be dependent on the force F normal to the shaft, the speed of rotation N of the shaft, the dynamic viscosity of the oil, and the shaft diameter D. Establish a correlation among these variables by using dimensional analysis.arrow_forwardA liquid of density ? and viscosity ? is pumped at volume flow rate V· through a pump of diameter D. The blades of the pump rotate at angular velocity ? . The pump supplies a pressure rise ΔP to the liquid. Using dimensional analysis, generate a dimensionless relationship for ΔP as a function of the other parameters in the problem. Identify any established nondimensional parameters that appear in your result. Hint: For consistency (and whenever possible), it is wise to choose a length, a density, and a velocity (or angular velocity) as repeating variables.arrow_forwardi need the answer quicklyarrow_forward
- The true optionarrow_forwardA- Womersley number (a) of a human aorta is 20 and for the rabbit aorta is 17, the blood density is approximately the same across the species. The values of viscosity were 0.0035 Ns/m² for the human and 0.0040 Ns/m² for the rabbit. The diameter of the aorta is 2.0 cm for the man, and 0.7 cm for the rabbit, estimate the heart rate beats per minute (bpm) for both speciesarrow_forwardplease do by buckingham's pi theoremarrow_forward
- 1. The thrust of a marine propeller Fr depends on water density p, propeller diameter D, speed of advance through the water V, acceleration due to gravity g, the angular speed of the propeller w, the water pressure p, and the water viscosity μ. You want to find a set of dimensionless variables on which the thrust coefficient depends. In other words CT = FT · = ƒen(#1, #2, ...) pV2D2 (a) What is k? Explain. (b) Find the 's on the right-hand-side of equation 1 if one of them HAS to be a Froude number gD/V², (1)arrow_forwardConsider laminar flow through a long section of pipe, as in Fig. For laminar flow it turns out that wall roughness is not a relevant parameter unless ? is very large. The volume flow rate V· through the pipe is a function of pipe diameter D, fluid viscosity ? , and axial pressure gradient dP/dx. If pipe diameter is doubled, all else being equal, by what factor will volume flow rate increase? Use dimensional analysis.arrow_forwardUsing II-Theorem method to Express (n) in terms of dimensionless groups.The efficiency (n) of a fan depends upon density (p), and dynamic viscosity (u), of the fluid, angular velocity (@), diameter of the rotator (D), and discharge (Q). Q3/ A petroleum crude oil having a kinematics viscosity 0.0001 m?/s is flowing through the piping arrangement shown in the below Figure,The total mass flow rate is equal 10 kg/s entering in pipe (A) . The flow divides to three pipes ( B, C, D). The steel pipes are schedule 40 pipe. note that the dynamic viscosity 0.088 kg/m.s. Calculate the following using SI units: 1- The type of flow in pipe (A). 2- The mass velocity in pipe (B) GB. 3- The velocity in pipe (D) Up. 4- The Volumetric flow rate in pipe (D) QD. 5- The Volumetric flow rate in pipe (C) Qc. Og = 2o mm Ug = 2UA Perolenm crude oIL A ma = 1o Kg/s O = 5o mm mic = ? Go = 7000 k9/m.s Nate that!- O, = 30 mm. D:0iameter. U:velocity G mass velocity mimass How vatearrow_forward
- Taylor number (Ta) is used here to describe the ratio between the inertia effect and the viscous effect. By applying Buckingham Pi's Theorem, determine an equation for Ta as a function of the radius of inner cylinder (r), cylinder tangential velocity (v), fluid dynamic viscosity (u), gap distance (L) and fluid density (p). Q4arrow_forwardThe Reynolds transport theorem (RTT) is discussed in Chap. 4 of your textbook. For the general case of a moving and/or deforming control volume, we write the RTT as follows: d pb dV + pbV-ñ dA dt dt dB sys where Vr is the relative velocity, i.e., the velocity of the fluid relative to the control surface. Write the primary dimensions of each additive term in the equation and verify that the equation is dimensionally homogeneous. Show all your work. (Hint: Since B can be any property of the flow-scalar, vector, or even tensor—it can have a variety of dimensions. So, just let the dimensions of B be those of B itself, {B}. Also, b is defined as B per unit mass.)arrow_forwardThis pleasearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning

Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Unit Conversion the Easy Way (Dimensional Analysis); Author: ketzbook;https://www.youtube.com/watch?v=HRe1mire4Gc;License: Standard YouTube License, CC-BY