EBK PRECALCULUS W/LIMITS
4th Edition
ISBN: 9781337516853
Author: Larson
Publisher: CENGAGE CO
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 7, Problem 16PS
(a)
To determine
The possible values of x and y for a healthy person.
(a)
Expert Solution
Answer to Problem 16PS
The possible values of x and y for a healthy person is
Explanation of Solution
Given:
Given that for a healthy person who is 4 feet and 10 inches tall, the minimum weight is 91 pounds and increases by 3.65 pounds for every additional inch of height. The maximum weight is about 119 pounds and increases by 4.85 pounds for every additional inch of height.
Formula used:
Comparing and forming the equation
Calculation:
To calculate the range of permitted weight range for the given height range. The minimum and maximum permitted for a person having 4feet and 10 inches and permitted increase of weight for every increased height in inches.
Given that for a healthy person who is 4 feet and 10 inches tall, the minimum weight is 91 pounds and increases by 3.65 pounds for every additional inch of height. The maximum weight is about 119 pounds and increases by 4.85 pounds for every additional inch of height.
(a)
The system of inequalities describing the relation if x denotes every additional increase of height and y is the weight. Also weight and increase it height cannot be negative.
The system of inequalities can be given as:
Conclusion:
The weight and increase in height cannot be negative. The possible values of x and y for a healthy person is
(b)
To determine
The graph of the system of inequalities.
(b)
Expert Solution
Answer to Problem 16PS
The system of inequalities are
Explanation of Solution
Given:
Given that for a healthy person who is 4 feet and 10 inches tall, the minimum weight is 91 pounds and increases by 3.65 pounds for every additional inch of height. The maximum weight is about 119 pounds and increases by 4.85 pounds for every additional inch of height
Formula used:
The substitution method is used
Calculation:
The system of inequalities can be given as:
The graph can be as shown below:
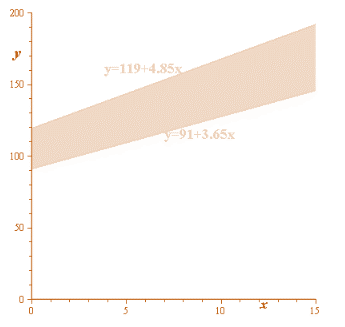
Conclusion:
The graph is the increasing function and it get increases.
(c)
To determine
The recommended weight range for a healthy person with 6 feet tall.
(c)
Expert Solution
Answer to Problem 16PS
The Minimum weight is l42.l pounds and maximum weight as l86.9 pounds.
Explanation of Solution
Given:
The recommended weight range for a healthy person with 6 feet tall.
Formula used:
The substitution method is used.
Calculation:
To find the recommended weight range for a person with 6 feet height
From 4 feet 10 inches to 6 feet, the x value should be 14, hence to find the values of minimum and maximum weight at
At
The Minimum weight is l42.l pounds and maximum weight as l86.9 pounds.
Conclusion:
The Minimum weight is l42.l pounds and maximum weight as l86.9 pounds.
Chapter 7 Solutions
EBK PRECALCULUS W/LIMITS
Ch. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10E
Ch. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Prob. 54ECh. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Prob. 60ECh. 7.1 - Prob. 61ECh. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.1 - Prob. 71ECh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Prob. 29ECh. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.2 - Prob. 63ECh. 7.2 - Prob. 64ECh. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Prob. 67ECh. 7.2 - Prob. 68ECh. 7.2 - Prob. 69ECh. 7.2 - Prob. 70ECh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Prob. 60ECh. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Prob. 63ECh. 7.3 - Prob. 64ECh. 7.3 - Prob. 65ECh. 7.3 - Prob. 66ECh. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - Prob. 71ECh. 7.3 - Prob. 72ECh. 7.3 - Prob. 73ECh. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7.4 - Prob. 53ECh. 7.4 - Prob. 54ECh. 7.4 - Prob. 55ECh. 7.4 - Prob. 56ECh. 7.4 - Prob. 57ECh. 7.4 - Prob. 58ECh. 7.4 - Prob. 59ECh. 7.4 - Prob. 60ECh. 7.4 - Prob. 61ECh. 7.4 - Prob. 62ECh. 7.4 - Prob. 63ECh. 7.4 - Prob. 64ECh. 7.4 - Prob. 65ECh. 7.4 - Prob. 66ECh. 7.5 - Prob. 1ECh. 7.5 - Prob. 2ECh. 7.5 - Prob. 3ECh. 7.5 - Prob. 4ECh. 7.5 - Prob. 5ECh. 7.5 - Prob. 6ECh. 7.5 - Prob. 7ECh. 7.5 - Prob. 8ECh. 7.5 - Prob. 9ECh. 7.5 - Prob. 10ECh. 7.5 - Prob. 11ECh. 7.5 - Prob. 12ECh. 7.5 - Prob. 13ECh. 7.5 - Prob. 14ECh. 7.5 - Prob. 15ECh. 7.5 - Prob. 16ECh. 7.5 - Prob. 17ECh. 7.5 - Prob. 18ECh. 7.5 - Prob. 19ECh. 7.5 - Prob. 20ECh. 7.5 - Prob. 21ECh. 7.5 - Prob. 22ECh. 7.5 - Prob. 23ECh. 7.5 - Prob. 24ECh. 7.5 - Prob. 25ECh. 7.5 - Prob. 26ECh. 7.5 - Prob. 27ECh. 7.5 - Prob. 28ECh. 7.5 - Prob. 29ECh. 7.5 - Prob. 30ECh. 7.5 - Prob. 31ECh. 7.5 - Prob. 32ECh. 7.5 - Prob. 33ECh. 7.5 - Prob. 34ECh. 7.5 - Prob. 35ECh. 7.5 - Prob. 36ECh. 7.5 - Prob. 37ECh. 7.5 - Prob. 38ECh. 7.5 - Prob. 39ECh. 7.5 - Prob. 40ECh. 7.5 - Prob. 41ECh. 7.5 - Prob. 42ECh. 7.5 - Prob. 43ECh. 7.5 - Prob. 44ECh. 7.5 - Prob. 45ECh. 7.5 - Prob. 46ECh. 7.5 - Prob. 47ECh. 7.5 - Prob. 48ECh. 7.5 - Prob. 49ECh. 7.5 - Prob. 50ECh. 7.5 - Prob. 51ECh. 7.5 - Prob. 52ECh. 7.5 - Prob. 53ECh. 7.5 - Prob. 54ECh. 7.5 - Prob. 55ECh. 7.5 - Prob. 56ECh. 7.5 - Prob. 57ECh. 7.5 - Prob. 58ECh. 7.5 - Prob. 59ECh. 7.5 - Prob. 60ECh. 7.5 - Prob. 61ECh. 7.5 - Prob. 62ECh. 7.5 - Prob. 63ECh. 7.5 - Prob. 64ECh. 7.5 - Prob. 65ECh. 7.5 - Prob. 66ECh. 7.5 - Prob. 67ECh. 7.5 - Prob. 68ECh. 7.5 - Prob. 69ECh. 7.5 - Prob. 70ECh. 7.5 - Prob. 71ECh. 7.5 - Prob. 72ECh. 7.5 - Prob. 73ECh. 7.5 - Prob. 74ECh. 7.5 - Prob. 75ECh. 7.5 - Prob. 76ECh. 7.6 - Prob. 1ECh. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - Prob. 4ECh. 7.6 - Prob. 5ECh. 7.6 - Prob. 6ECh. 7.6 - Prob. 7ECh. 7.6 - Prob. 8ECh. 7.6 - Prob. 9ECh. 7.6 - Prob. 10ECh. 7.6 - Prob. 11ECh. 7.6 - Prob. 12ECh. 7.6 - Prob. 13ECh. 7.6 - Prob. 14ECh. 7.6 - Prob. 15ECh. 7.6 - Prob. 16ECh. 7.6 - Prob. 17ECh. 7.6 - Prob. 18ECh. 7.6 - Prob. 19ECh. 7.6 - Prob. 20ECh. 7.6 - Prob. 21ECh. 7.6 - Prob. 22ECh. 7.6 - Prob. 23ECh. 7.6 - Prob. 24ECh. 7.6 - Prob. 25ECh. 7.6 - Prob. 26ECh. 7.6 - Prob. 27ECh. 7.6 - Prob. 28ECh. 7.6 - Prob. 29ECh. 7.6 - Prob. 30ECh. 7.6 - Prob. 31ECh. 7.6 - Prob. 32ECh. 7.6 - Prob. 33ECh. 7.6 - Prob. 34ECh. 7.6 - Prob. 35ECh. 7.6 - Prob. 36ECh. 7.6 - Prob. 37ECh. 7.6 - Prob. 38ECh. 7.6 - Prob. 39ECh. 7.6 - Prob. 40ECh. 7.6 - Prob. 41ECh. 7.6 - Prob. 42ECh. 7.6 - Prob. 43ECh. 7.6 - Prob. 44ECh. 7.6 - Prob. 45ECh. 7.6 - Prob. 46ECh. 7.6 - Prob. 47ECh. 7.6 - Prob. 48ECh. 7.6 - Prob. 49ECh. 7.6 - Prob. 50ECh. 7.6 - Prob. 51ECh. 7 - Prob. 1RECh. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RECh. 7 - Prob. 82RECh. 7 - Prob. 83RECh. 7 - Prob. 84RECh. 7 - Prob. 85RECh. 7 - Prob. 86RECh. 7 - Prob. 87RECh. 7 - Prob. 88RECh. 7 - Prob. 89RECh. 7 - Prob. 90RECh. 7 - Prob. 91RECh. 7 - Prob. 92RECh. 7 - Prob. 93RECh. 7 - Prob. 94RECh. 7 - Prob. 95RECh. 7 - Prob. 96RECh. 7 - Prob. 97RECh. 7 - Prob. 98RECh. 7 - Prob. 99RECh. 7 - Prob. 100RECh. 7 - Prob. 101RECh. 7 - Prob. 102RECh. 7 - Prob. 103RECh. 7 - Prob. 104RECh. 7 - Prob. 1CTCh. 7 - Prob. 2CTCh. 7 - Prob. 3CTCh. 7 - Prob. 4CTCh. 7 - Prob. 5CTCh. 7 - Prob. 6CTCh. 7 - Prob. 7CTCh. 7 - Prob. 8CTCh. 7 - Prob. 9CTCh. 7 - Prob. 10CTCh. 7 - Prob. 11CTCh. 7 - Prob. 12CTCh. 7 - Prob. 13CTCh. 7 - Prob. 14CTCh. 7 - Prob. 15CTCh. 7 - Prob. 16CTCh. 7 - Prob. 17CTCh. 7 - Prob. 18CTCh. 7 - Prob. 19CTCh. 7 - Prob. 20CTCh. 7 - Prob. 21CTCh. 7 - Prob. 1PSCh. 7 - Prob. 2PSCh. 7 - Prob. 3PSCh. 7 - Prob. 4PSCh. 7 - Prob. 5PSCh. 7 - Prob. 6PSCh. 7 - Prob. 7PSCh. 7 - Prob. 8PSCh. 7 - Prob. 9PSCh. 7 - Prob. 10PSCh. 7 - Prob. 11PSCh. 7 - Prob. 12PSCh. 7 - Prob. 13PSCh. 7 - Prob. 14PSCh. 7 - Prob. 15PSCh. 7 - Prob. 16PSCh. 7 - Prob. 17PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- question 10 pleasearrow_forward00 (a) Starting with the geometric series Σ X^, find the sum of the series n = 0 00 Σηχη - 1, |x| < 1. n = 1 (b) Find the sum of each of the following series. 00 Σnx", n = 1 |x| < 1 (ii) n = 1 sin (c) Find the sum of each of the following series. (i) 00 Σn(n-1)x^, |x| <1 n = 2 (ii) 00 n = 2 n² - n 4n (iii) M8 n = 1 շոarrow_forward(a) Use differentiation to find a power series representation for 1 f(x) = (4 + x)²* f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (b) Use part (a) to find a power series for f(x) = 1 (4 + x)³° f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (c) Use part (b) to find a power series for f(x) = x² (4 + x)³* 00 f(x) = Σ n = 2 What is the radius of convergence, R? R = Need Help? Read It Watch It SUBMIT ANSWERarrow_forward
- answer for question 4 pleasearrow_forward(3) (20 points) Let F(x, y, z) = (y, z, x²z). Define E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}. (a) (2 points) Calculate the divergence V. F. (b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that the triple integral √ (V · F) dV = √ 2²(1. = x²(1 − x² - y²) dA. Earrow_forward(2) (22 points) Let F(x, y, z) = (x sin y, cos y, ―xy). (a) (2 points) Calculate V. F. (b) (6 points) Given a vector field is everywhere defined with V G₁(x, y, z) = * G2(x, y, z) = − G3(x, y, z) = 0. 0 0 F(x, y, z) = (F₁(x, y, z), F₂(x, y, z), F(x, y, z)) that F = 0, let G = (G1, G2, G3) where F₂(x, y, y, t) dt - √ F³(x, t, 0) dt, * F1(x, y, t) dt, t) dt - √ F Calculate G for the vector field F(x, y, z) = (x sin y, cos y, -xy).arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √(x + y) A R R = {(x, y) | 25 < x² + y² ≤ 36, x < 0} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardFind the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). R - 1 · {(r,0) | 1 ≤ r≤ 5,½π≤ 0<1π}. Hint: Be sure to convert to Polar coordinates. Use the correct differential for Polar Coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √2(x+y) dA R R = {(x, y) | 4 < x² + y² < 25,0 < x} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardHW: The frame shown in the figure is pinned at A and C. Use moment distribution method, with and without modifications, to draw NFD, SFD, and BMD. B I I 40 kN/m A 3 m 4 marrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY