
Concept explainers
a.
To calculate: To find the system of equations such that one equation represents the total amount of the final mixture required and the other represents the percent of acid in the final mixture.
a.
Answer to Problem 49E
Explanation of Solution
Given information:
Given that thirty liters of a 40% acid solution is obtained by mixing a 25 % solution with a 50% solution.
Calculation:
Let x and y represent the amounts of the 25% and 50% solutions respectively used to make the 40% solution.
So the total amount of solution is given by:
Amount of acid in x liters of 25% solution is given by:
Similarly amount of acid in y liters of 50% solution is given by:
Also the amount of acid in 30 liters of 40% solution is given by:
Hence the amount of acid in final solution is represented by the equation:
Therefore the required equations representing the given system are:
b.
To graph: To plot the two equations on the same graph and check how amount of 50% solution changes as amount of 25% solution changes.
b.
Explanation of Solution
Given information:
Given that thirty liters of a 40% acid solution is obtained by mixing a 25 % solution with a 50% solution.
x and y represent the amounts of the 25% and 50% solutions respectively used to make the 40% solution.
The equations are:
Graph:
Plotting the equations on a graph with x and y as the axes:
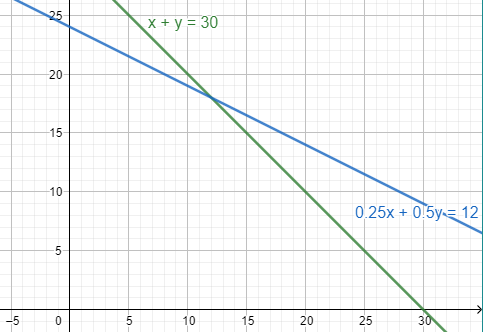
Interpretation:
From the graph it is seen that in both the cases i.e. for both the equations as x increasesy decreases.
Hence, the amount of 50% solution decreases as amount of 25% solution changes.
c.
To calculate: To find the quantity of each solution required to obtain the final mixture.
c.
Answer to Problem 49E
Explanation of Solution
Given information:
Given that thirty liters of a 40% acid solution is obtained by mixing a 25 % solution with a 50% solution.
Calculation:
From the graph it is seen that both the lines meet at a point where
Therefore the quantities of the solutions required are:
i.e. 12 liters of 25% solutions and 18 liters of 50% solution
Chapter 7 Solutions
EBK PRECALCULUS W/LIMITS
- Pls help ASAParrow_forward9. a) Determie values of a and b so that the function is continuous. ax - 2b f(x) 2 x≤-2 -2x+a, x ≥2 \-ax² - bx + 1, −2 < x < 2) 9b) Consider f(x): = 2x²+x-3 x-b and determine all the values of b such that f(x) does not have a vertical asymptote. Show work.arrow_forwardPls help ASAParrow_forward
- 3. True False. If false create functions that prove it is false. Note: f(x) = g(x). a) If_lim ƒ(x) = ∞ and_lim g(x) = ∞,then_lim [ƒ(x) − g(x)] = 0 x→ 0+ x→0+ x→0+ b) If h(x) and g(x) are continuous at x = c, and if h(c) > 0 and g(c) = 0, then h(x) lim. will = x→c g(x) c) If lim f(x) = 0 and lim g(x) = 0 then lim f(x) does not exist. x-a x-a x→a g(x)arrow_forwardPls help ASAParrow_forward15. a) Consider f(x) = x-1 3x+2 and use the difference quotient to determine the simplified expression in terms of x, for the slope of any tangent to y = f(x). Also, determine the slope at x = 2. 15 b) Determine the equation of the tangent to f(x) at x = 2. Final answer in Standard Form Ax + By + C = 0, A ≥ 0, with no fractions or decimals.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





