EBK PRECALCULUS W/LIMITS
4th Edition
ISBN: 9781337516853
Author: Larson
Publisher: CENGAGE CO
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 7.5, Problem 69E
(a)
To determine
To graph: A system of inequalities for different amount of food X and food Ywith the help of prescribed plan by dietician.
(a)
Expert Solution
Explanation of Solution
Given:
The maximum weight to hold the weight in the truck is 7500 pounds. A warehouse requires at least 50 packages to ship of 55 pounds and at least 40 bags of stone to ship of 70 pounds.
Graph:
Consider x as the amount of 55lb bags and y as the amount of 70lb bags.
The maximum weight to hold the weight in the truck is 7500 pounds. A warehouse requires at least 50 packages to ship of 55 pounds and at least 40 bags of stone to ship of 70 pounds.
As per the given information, the inequalities are set up as follows:
Draw the graph with the help of lines
Find the coordinates of the line
Substitute
Further simplify the above calculation.
Substitute
The coordinates are
Shade the region above the lines for the sign of at least and shade the region below the line for the sign of at most in three inequalities.
Now draw the graph with the help of obtained coordinates of the lines.
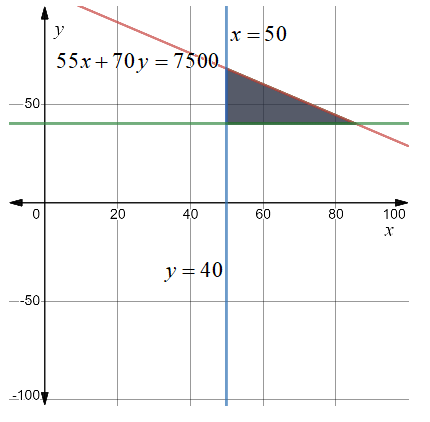
Figure 1
Interpretation:
It can be observed from the graph that the shaded region lies in the first quadrant.
(b)
To determine
To find: Two solutions from and interpret the result.
(b)
Expert Solution
Explanation of Solution
Solutions of the system of inequalities are those points that comes under the feasible region of the graph.
The feasible region of the graph is the shaded region of the graph.
Take any two points from the shaded region of the graph.
It can be seen from the graph that the points
The point
The point
Chapter 7 Solutions
EBK PRECALCULUS W/LIMITS
Ch. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10E
Ch. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Prob. 54ECh. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Prob. 60ECh. 7.1 - Prob. 61ECh. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.1 - Prob. 71ECh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Prob. 29ECh. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.2 - Prob. 63ECh. 7.2 - Prob. 64ECh. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Prob. 67ECh. 7.2 - Prob. 68ECh. 7.2 - Prob. 69ECh. 7.2 - Prob. 70ECh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Prob. 60ECh. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Prob. 63ECh. 7.3 - Prob. 64ECh. 7.3 - Prob. 65ECh. 7.3 - Prob. 66ECh. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - Prob. 71ECh. 7.3 - Prob. 72ECh. 7.3 - Prob. 73ECh. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7.4 - Prob. 53ECh. 7.4 - Prob. 54ECh. 7.4 - Prob. 55ECh. 7.4 - Prob. 56ECh. 7.4 - Prob. 57ECh. 7.4 - Prob. 58ECh. 7.4 - Prob. 59ECh. 7.4 - Prob. 60ECh. 7.4 - Prob. 61ECh. 7.4 - Prob. 62ECh. 7.4 - Prob. 63ECh. 7.4 - Prob. 64ECh. 7.4 - Prob. 65ECh. 7.4 - Prob. 66ECh. 7.5 - Prob. 1ECh. 7.5 - Prob. 2ECh. 7.5 - Prob. 3ECh. 7.5 - Prob. 4ECh. 7.5 - Prob. 5ECh. 7.5 - Prob. 6ECh. 7.5 - Prob. 7ECh. 7.5 - Prob. 8ECh. 7.5 - Prob. 9ECh. 7.5 - Prob. 10ECh. 7.5 - Prob. 11ECh. 7.5 - Prob. 12ECh. 7.5 - Prob. 13ECh. 7.5 - Prob. 14ECh. 7.5 - Prob. 15ECh. 7.5 - Prob. 16ECh. 7.5 - Prob. 17ECh. 7.5 - Prob. 18ECh. 7.5 - Prob. 19ECh. 7.5 - Prob. 20ECh. 7.5 - Prob. 21ECh. 7.5 - Prob. 22ECh. 7.5 - Prob. 23ECh. 7.5 - Prob. 24ECh. 7.5 - Prob. 25ECh. 7.5 - Prob. 26ECh. 7.5 - Prob. 27ECh. 7.5 - Prob. 28ECh. 7.5 - Prob. 29ECh. 7.5 - Prob. 30ECh. 7.5 - Prob. 31ECh. 7.5 - Prob. 32ECh. 7.5 - Prob. 33ECh. 7.5 - Prob. 34ECh. 7.5 - Prob. 35ECh. 7.5 - Prob. 36ECh. 7.5 - Prob. 37ECh. 7.5 - Prob. 38ECh. 7.5 - Prob. 39ECh. 7.5 - Prob. 40ECh. 7.5 - Prob. 41ECh. 7.5 - Prob. 42ECh. 7.5 - Prob. 43ECh. 7.5 - Prob. 44ECh. 7.5 - Prob. 45ECh. 7.5 - Prob. 46ECh. 7.5 - Prob. 47ECh. 7.5 - Prob. 48ECh. 7.5 - Prob. 49ECh. 7.5 - Prob. 50ECh. 7.5 - Prob. 51ECh. 7.5 - Prob. 52ECh. 7.5 - Prob. 53ECh. 7.5 - Prob. 54ECh. 7.5 - Prob. 55ECh. 7.5 - Prob. 56ECh. 7.5 - Prob. 57ECh. 7.5 - Prob. 58ECh. 7.5 - Prob. 59ECh. 7.5 - Prob. 60ECh. 7.5 - Prob. 61ECh. 7.5 - Prob. 62ECh. 7.5 - Prob. 63ECh. 7.5 - Prob. 64ECh. 7.5 - Prob. 65ECh. 7.5 - Prob. 66ECh. 7.5 - Prob. 67ECh. 7.5 - Prob. 68ECh. 7.5 - Prob. 69ECh. 7.5 - Prob. 70ECh. 7.5 - Prob. 71ECh. 7.5 - Prob. 72ECh. 7.5 - Prob. 73ECh. 7.5 - Prob. 74ECh. 7.5 - Prob. 75ECh. 7.5 - Prob. 76ECh. 7.6 - Prob. 1ECh. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - Prob. 4ECh. 7.6 - Prob. 5ECh. 7.6 - Prob. 6ECh. 7.6 - Prob. 7ECh. 7.6 - Prob. 8ECh. 7.6 - Prob. 9ECh. 7.6 - Prob. 10ECh. 7.6 - Prob. 11ECh. 7.6 - Prob. 12ECh. 7.6 - Prob. 13ECh. 7.6 - Prob. 14ECh. 7.6 - Prob. 15ECh. 7.6 - Prob. 16ECh. 7.6 - Prob. 17ECh. 7.6 - Prob. 18ECh. 7.6 - Prob. 19ECh. 7.6 - Prob. 20ECh. 7.6 - Prob. 21ECh. 7.6 - Prob. 22ECh. 7.6 - Prob. 23ECh. 7.6 - Prob. 24ECh. 7.6 - Prob. 25ECh. 7.6 - Prob. 26ECh. 7.6 - Prob. 27ECh. 7.6 - Prob. 28ECh. 7.6 - Prob. 29ECh. 7.6 - Prob. 30ECh. 7.6 - Prob. 31ECh. 7.6 - Prob. 32ECh. 7.6 - Prob. 33ECh. 7.6 - Prob. 34ECh. 7.6 - Prob. 35ECh. 7.6 - Prob. 36ECh. 7.6 - Prob. 37ECh. 7.6 - Prob. 38ECh. 7.6 - Prob. 39ECh. 7.6 - Prob. 40ECh. 7.6 - Prob. 41ECh. 7.6 - Prob. 42ECh. 7.6 - Prob. 43ECh. 7.6 - Prob. 44ECh. 7.6 - Prob. 45ECh. 7.6 - Prob. 46ECh. 7.6 - Prob. 47ECh. 7.6 - Prob. 48ECh. 7.6 - Prob. 49ECh. 7.6 - Prob. 50ECh. 7.6 - Prob. 51ECh. 7 - Prob. 1RECh. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RECh. 7 - Prob. 82RECh. 7 - Prob. 83RECh. 7 - Prob. 84RECh. 7 - Prob. 85RECh. 7 - Prob. 86RECh. 7 - Prob. 87RECh. 7 - Prob. 88RECh. 7 - Prob. 89RECh. 7 - Prob. 90RECh. 7 - Prob. 91RECh. 7 - Prob. 92RECh. 7 - Prob. 93RECh. 7 - Prob. 94RECh. 7 - Prob. 95RECh. 7 - Prob. 96RECh. 7 - Prob. 97RECh. 7 - Prob. 98RECh. 7 - Prob. 99RECh. 7 - Prob. 100RECh. 7 - Prob. 101RECh. 7 - Prob. 102RECh. 7 - Prob. 103RECh. 7 - Prob. 104RECh. 7 - Prob. 1CTCh. 7 - Prob. 2CTCh. 7 - Prob. 3CTCh. 7 - Prob. 4CTCh. 7 - Prob. 5CTCh. 7 - Prob. 6CTCh. 7 - Prob. 7CTCh. 7 - Prob. 8CTCh. 7 - Prob. 9CTCh. 7 - Prob. 10CTCh. 7 - Prob. 11CTCh. 7 - Prob. 12CTCh. 7 - Prob. 13CTCh. 7 - Prob. 14CTCh. 7 - Prob. 15CTCh. 7 - Prob. 16CTCh. 7 - Prob. 17CTCh. 7 - Prob. 18CTCh. 7 - Prob. 19CTCh. 7 - Prob. 20CTCh. 7 - Prob. 21CTCh. 7 - Prob. 1PSCh. 7 - Prob. 2PSCh. 7 - Prob. 3PSCh. 7 - Prob. 4PSCh. 7 - Prob. 5PSCh. 7 - Prob. 6PSCh. 7 - Prob. 7PSCh. 7 - Prob. 8PSCh. 7 - Prob. 9PSCh. 7 - Prob. 10PSCh. 7 - Prob. 11PSCh. 7 - Prob. 12PSCh. 7 - Prob. 13PSCh. 7 - Prob. 14PSCh. 7 - Prob. 15PSCh. 7 - Prob. 16PSCh. 7 - Prob. 17PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- A function is defined on the interval (-π/2,π/2) by this multipart rule: if -π/2 < x < 0 f(x) = a if x=0 31-tan x +31-cot x if 0 < x < π/2 Here, a and b are constants. Find a and b so that the function f(x) is continuous at x=0. a= b= 3arrow_forwardUse the definition of continuity and the properties of limits to show that the function is continuous at the given number a. f(x) = (x + 4x4) 5, a = -1 lim f(x) X--1 = lim x+4x X--1 lim X-1 4 x+4x 5 ))" 5 )) by the power law by the sum law lim (x) + lim X--1 4 4x X-1 -(0,00+( Find f(-1). f(-1)=243 lim (x) + -1 +4 35 4 ([ ) lim (x4) 5 x-1 Thus, by the definition of continuity, f is continuous at a = -1. by the multiple constant law by the direct substitution propertyarrow_forward1. Compute Lo F⚫dr, where and C is defined by F(x, y) = (x² + y)i + (y − x)j r(t) = (12t)i + (1 − 4t + 4t²)j from the point (1, 1) to the origin.arrow_forward
- 2. Consider the vector force: F(x, y, z) = 2xye²i + (x²e² + y)j + (x²ye² — z)k. (A) [80%] Show that F satisfies the conditions for a conservative vector field, and find a potential function (x, y, z) for F. Remark: To find o, you must use the method explained in the lecture. (B) [20%] Use the Fundamental Theorem for Line Integrals to compute the work done by F on an object moves along any path from (0,1,2) to (2, 1, -8).arrow_forwardhelp pleasearrow_forwardIn each of Problems 1 through 4, draw a direction field for the given differential equation. Based on the direction field, determine the behavior of y as t → ∞. If this behavior depends on the initial value of y at t = 0, describe the dependency.1. y′ = 3 − 2yarrow_forward
- B 2- The figure gives four points and some corresponding rays in the xy-plane. Which of the following is true? A B Angle COB is in standard position with initial ray OB and terminal ray OC. Angle COB is in standard position with initial ray OC and terminal ray OB. C Angle DOB is in standard position with initial ray OB and terminal ray OD. D Angle DOB is in standard position with initial ray OD and terminal ray OB.arrow_forwardtemperature in degrees Fahrenheit, n hours since midnight. 5. The temperature was recorded at several times during the day. Function T gives the Here is a graph for this function. To 29uis a. Describe the overall trend of temperature throughout the day. temperature (Fahrenheit) 40 50 50 60 60 70 5 10 15 20 25 time of day b. Based on the graph, did the temperature change more quickly between 10:00 a.m. and noon, or between 8:00 p.m. and 10:00 p.m.? Explain how you know. (From Unit 4, Lesson 7.) 6. Explain why this graph does not represent a function. (From Unit 4, Lesson 8.)arrow_forwardFind the area of the shaded region. (a) 5- y 3 2- (1,4) (5,0) 1 3 4 5 6 (b) 3 y 2 Decide whether the problem can be solved using precalculus, or whether calculus is required. If the problem can be solved using precalculus, solve it. If the problem seems to require calculus, use a graphical or numerical approach to estimate the solution. STEP 1: Consider the figure in part (a). Since this region is simply a triangle, you may use precalculus methods to solve this part of the problem. First determine the height of the triangle and the length of the triangle's base. height 4 units units base 5 STEP 2: Compute the area of the triangle by employing a formula from precalculus, thus finding the area of the shaded region in part (a). 10 square units STEP 3: Consider the figure in part (b). Since this region is defined by a complicated curve, the problem seems to require calculus. Find an approximation of the shaded region by using a graphical approach. (Hint: Treat the shaded regi as…arrow_forward
- Solve this differential equation: dy 0.05y(900 - y) dt y(0) = 2 y(t) =arrow_forwardSuppose that you are holding your toy submarine under the water. You release it and it begins to ascend. The graph models the depth of the submarine as a function of time. What is the domain and range of the function in the graph? 1- t (time) 1 2 4/5 6 7 8 -2 -3 456700 -4 -5 -6 -7 d (depth) -8 D: 00 t≤ R:arrow_forward0 5 -1 2 1 N = 1 to x = 3 Based on the graph above, estimate to one decimal place the average rate of change from x =arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY