
a)
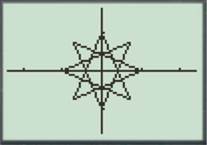
To visualize: The eight-eight roots of the unity.
The traced points are shown in figure (1).
Given information:
It is given that
Calculation:
By following the instructions, calculator should display
Using the TRACE feature gives the roots where
Trace the points
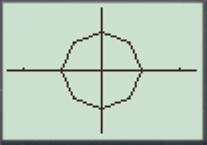
Figure (1)
Therefore, the traced points are shown in figure (1).
b)
To find: Whether the other generates the eighth roots of unity.
Yes, the other generates the eighth roots of unity.
Calculation:
The arguments of the eighth roots differ by
For
Enter the number as shown below.
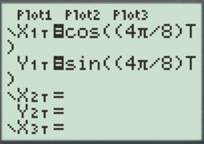
Press the GRAPH button to obtain the graph as shown below.
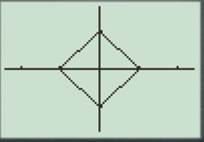
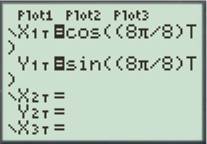
For
Enter the number as shown below.
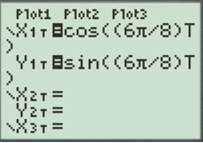
Press the GRAPH button to obtain the graph as shown below.
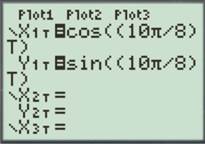
For
Enter the number as shown below.
Press the GRAPH button to obtain the graph as shown below.

For
Enter the number as shown below.
Press the GRAPH button to obtain the graph as shown below.

For
Enter the number as shown below.
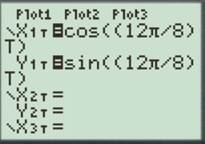
Press the GRAPH button to obtain the graph as shown below.
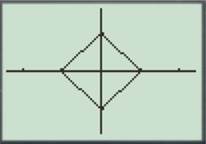
For
Enter the number as shown below.
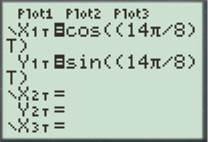
Press the GRAPH button to obtain the graph as shown below.
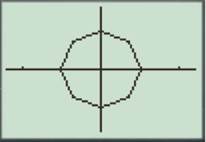
For
Enter the number as shown below.

Press the GRAPH button to obtain the graph as shown below.
Therefore, yes, the other generates the eighth roots of unity.
c)
To repeat: The above process for the fifth, sixth, and seventh roots of unity.
All the roots are traced below.
Given information:
The complex number is
Calculation:
For the fifth roots, use the argument
Among these, three more arguments generate the fifth roots of unity which are as follows.
For
Enter the number as shown below.
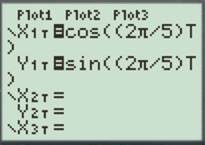
Press the GRAPH button to obtain the graph as shown below.
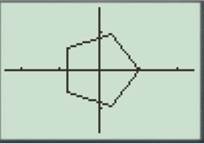
For
Enter the number as shown below.
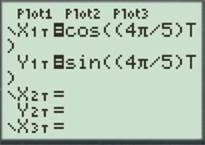
Press the GRAPH button to obtain the graph as shown below.
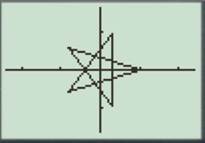
For
Enter the number as shown below.
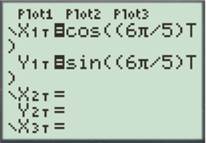
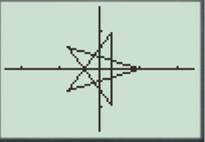
Press the GRAPH button to obtain the graph as shown below.
For
Enter the number as shown below.
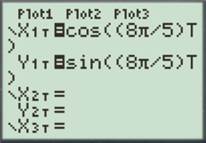
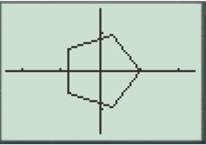
Press the GRAPH button to obtain the graph as shown below.
For
Enter the number as shown below.
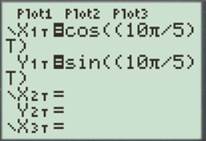
Press the GRAPH button to obtain the graph as shown below.
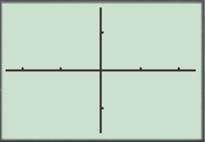
For the sixth roots, use the argument
Among these, one more arguments generate the sixth roots of unity which is as follows.
For
Enter the number as shown below.
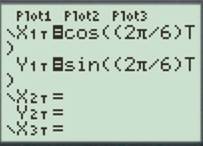
Press the GRAPH button to obtain the graph as shown below.
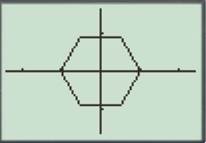
For
Enter the number as shown below.
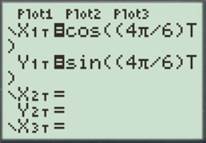
Press the GRAPH button to obtain the graph as shown below.
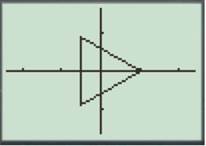
For
Enter the number as shown below.
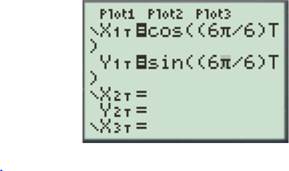
Press the GRAPH button to obtain the graph as shown below.
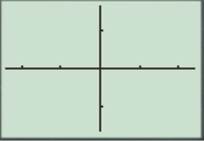
For
Enter the number as shown below.
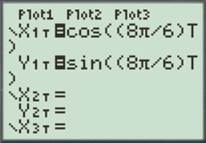
Press the GRAPH button to obtain the graph as shown below.
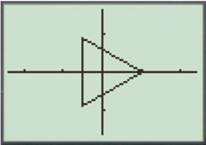
For
Enter the number as shown below.
Press the GRAPH button to obtain the graph as shown below.

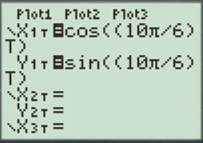
For
Enter the number as shown below.
Press the GRAPH button to obtain the graph as shown below.

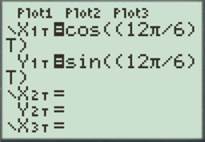
For the seventh roots, use the argument
Among these, five more arguments generate the seventh roots of unity which are as follows.
For
Enter the number as shown below.
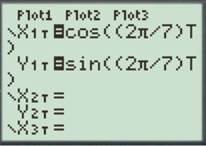
Press the GRAPH button to obtain the graph as shown below.
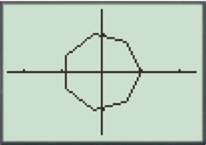
For
Enter the number as shown below.
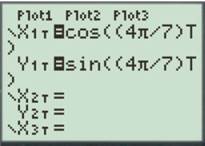
Press the GRAPH button to obtain the graph as shown below.
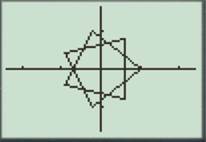
For
Enter the number as shown below.

Press the GRAPH button to obtain the graph as shown below.
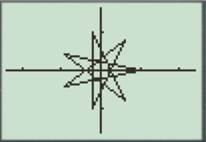
For
Enter the number as shown below.

Press the GRAPH button to obtain the graph as shown below.
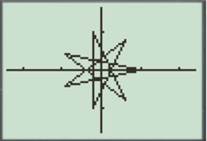
For
Enter the number as shown below.
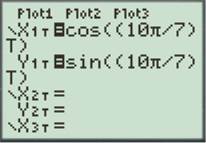
Press the GRAPH button to obtain the graph as shown below.
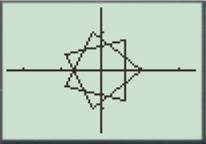
For
Enter the number as shown below.

Press the GRAPH button to obtain the graph as shown below.

For
Enter the number as shown below.

Press the GRAPH button to obtain the graph as shown below.
Therefore, all the roots are shown above.
d)
To write: The conjecture about an nth root of unity that generates all the nth roots of unity.
All the
Calculation:
The
Therefore, all the
Chapter 6 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
- 1. A bicyclist is riding their bike along the Chicago Lakefront Trail. The velocity (in feet per second) of the bicyclist is recorded below. Use (a) Simpson's Rule, and (b) the Trapezoidal Rule to estimate the total distance the bicyclist traveled during the 8-second period. t 0 2 4 6 8 V 10 15 12 10 16 2. Find the midpoint rule approximation for (a) n = 4 +5 x²dx using n subintervals. 1° 2 (b) n = 8 36 32 28 36 32 28 24 24 20 20 16 16 12 8- 4 1 2 3 4 5 6 12 8 4 1 2 3 4 5 6arrow_forward= 5 37 A 4 8 0.5 06 9arrow_forwardConsider the following system of equations, Ax=b : x+2y+3z - w = 2 2x4z2w = 3 -x+6y+17z7w = 0 -9x-2y+13z7w = -14 a. Find the solution to the system. Write it as a parametric equation. You can use a computer to do the row reduction. b. What is a geometric description of the solution? Explain how you know. c. Write the solution in vector form? d. What is the solution to the homogeneous system, Ax=0?arrow_forward
- 2. Find a matrix A with the following qualities a. A is 3 x 3. b. The matrix A is not lower triangular and is not upper triangular. c. At least one value in each row is not a 1, 2,-1, -2, or 0 d. A is invertible.arrow_forwardFind the exact area inside r=2sin(2\theta ) and outside r=\sqrt(3)arrow_forwardA 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forward
- Explain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forwarduse Cauchy Mean-Value Theorem to derive Corollary 12.6.2, and then derive 12.6.3arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





