
a.
To write an equation that models the height of the arrow as a function of
Given information:
A person shoots the arrow with an initial velocity 245 ft/sec straight up. The arrow leaves from a point 200 ft above the ground level.
Calculation:
Since the initial velocity is 245 and the arrow leaves from a height of 200 ft, the equation modeling the height of the arrow at any time
Conclusion:
The required equation that models the height of the arrow is
b.
To write a parametric equation to simulate the height of the flight of the arrow.
The parametric equation that simulates the height of the flight of the arrow is
Given information:
A person shoots the arrow with an initial velocity 245 ft/sec straight up. The arrow leaves from a point 200 ft above the ground level.
Calculation:
The equation modeling the height of the arrow at any time
The parametric equation that simulates the height of the flight can be given as:
Conclusion:
The parametric equation that simulates the height of the flight of the arrow is
c.
To graph the parametric equation that models the height of the arrow.
Given information:
A person shoots the arrow with an initial velocity 245 ft/sec straight up. The arrow leaves from a point 200 ft above the ground level.
Calculation:
The parametric equation that simulates the height of the flight can be given as:
Use a graphing calculator to graph the equation as shown below.
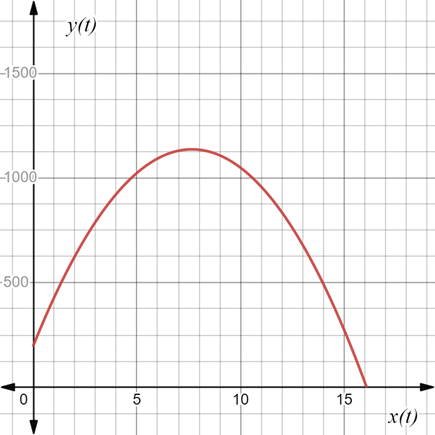
d.
To find the heigh of the arrow after 4 sec.
The parametric equation that simulates the height of the flight of the arrow is
Given information:
A person shoots the arrow with an initial velocity 245 ft/sec straight up. The arrow leaves from a point 200 ft above the ground level.
Calculation:
The equation modeling the height of the arrow at any time
Substitute
Conclusion:
The height of the arrow after 4 sec is 924 ft.
e.
To find the time when the arrow hits the ground.
Given information:
A person shoots the arrow with an initial velocity 245 ft/sec straight up. The arrow leaves from a point 200 ft above the ground level.
Calculation:
The equation modeling the height of the arrow at any time
When arrow hits the ground,
So, solve the equation
Since the cannot be negative, the value
Conclusion:
The arrow takes
Chapter 6 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
- Determine whether the series is convergent or divergent. Justify your answer. If the series is convergent, you do not have to find its sum. n=0 (-1) 72n+1 (2n)!arrow_forward+ Find the first five non-zero terms of the Taylor series for f(x) = sin(2x) centered at 4π. + + + ...arrow_forward+ + ... Find the first five non-zero terms of the Taylor series for f(x) centered at x = 4. = 1 x + + +arrow_forward
- Find the interval and radius of convergence for the given power series. n=0 (− 1)" xn 7" (n² + 2) The series is convergent on the interval: The radius of convergence is R =arrow_forwardFind the interval and radius of convergence for the given power series. n=1 (x-4)" n( - 8)" The series is convergent on the interval: The radius of convergence is R =arrow_forwardFind the interval and radius of convergence for the given power series. n=0 10"x" 7(n!) The series is convergent on the interval: The radius of convergence is R =arrow_forward
- Consider the electrical circuit shown in Figure P6-41. It consists of two closed loops. Taking the indicated directions of the currents as positive, obtain the differential equations governing the currents I1 and I2 flowing through the resistor R and inductor L, respectively.arrow_forwardCalculus lll May I please have the semicolon statements in the boxes explained and completed? Thank you so mucharrow_forwardCalculus lll May I please have the solution for the example? Thank youarrow_forward
- 4. AP CalagaBourd Ten the g stem for 00 3B Quiz 3. The point P has polar coordinates (10, 5). Which of the following is the location of point P in rectangular coordinates? (A) (-5√3,5) (B) (-5,5√3) (C) (5√3,5) (D) (5√3,-5) 7A 6 2 3 4 S 元 3 داند 4/6 Polar axis -0 11 2 3 4 4 5л 3 Зл 2 11π 6 rectangular coordinates of K? The figure shows the polar coordinate system with point P labeled. Point P is rotated an angle of measure clockwise about the origin. The image of this transformation is at the location K (not shown). What are the (A) (-2,2√3) (B) (-2√3,2) (C) (2,-2√3) D) (2√3,-2) T 2arrow_forwardAP CollegeBoard 3B Quiz 1. 2. y AP PRECALCULUS Name: od to dove (or) slog mig Test Boc 2л The figure gives the graphs of four functions labeled A, B, C, and D -1 in the xy-plane. Which is the graph of f(x) = 2 cos¹x ? m -3 π y 2- 1 3 (A) A (B) B 2 A B C D D -1- -2- Graph of f -2 -1 3. 2- y' Graph of g 1 2 1 3 y = R 2/01 y = 1 + 1/2 2 3 4 5 y= = 1-777 2 (C) C (D) D Which of the following defines g(x)? The figure gives the graphs of the functions ƒ and g in the xy-plane. The function f is given by f(x) = tan-1 EVES) (A) (A) tan¹x+1 (B) tan¹ x + 1/ (C) tan¹ (2) +1 (D) tan¹() + (B) Vs) a I.arrow_forwardConsider the region below f(x) = (11-x), above the x-axis, and between x = 0 and x = 11. Let x; be the midpoint of the ith subinterval. Complete parts a. and b. below. a. Approximate the area of the region using eleven rectangles. Use the midpoints of each subinterval for the heights of the rectangles. The area is approximately square units. (Type an integer or decimal.)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





