Chapter 6.6, Problem 32IP

a.

To determine

To find: Copy and complete the table.

Answer to Problem 32IP

Years	Ben	Anica
2	$66	$67.98
4	$\$132$	$\$144.37$
6	$\$198$	$\$230.19$
8	$\$264$	$\$326.62$
10	$\$330$	$\$434.97$

Explanation of Solution

Given information:

Principal amount of Ben $=\$550$

Simple interest percent of Ben $=6\%$

Principal amount of Anica $=\$550$ .

Compound Interest percent of Anica $=6\%$

If compounded annually value of $n$ is $1$ .

Concept:

Simple interest:

  $I=prt$

Where

  $I=$ Simple interest.

  $p=$ Principal amount

  $t=$ time in years.

  $r=$ Annual interest rate.

Compound interest:

  $A=p{\left(1+\frac{r}{n}\right)}^{nt}$

Where

  $A=$ Total amount

  $p=$ Principal amount

  $t=$ time in years.

  $r=$ Annual interest rate.

  $n=1$ for compounded annually.

Calculation:

Using simple interest for Ben when $t=2$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=R=6\%$

We know

Annual interest rate $=r=\frac{R}{100}$

  $\begin{array}{l}\Rightarrow r=\frac{6}{100}\\ \Rightarrow r=0.06\end{array}$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}I=prt\\ \Rightarrow I=\left(550\right)\left(0.06\right)\left(2\right)\\ \Rightarrow I=66\end{array}$

Therefore,

Final amount $=$ Principal amount $+$ Simple interest.

  $\Rightarrow$ Final amount $=$$550+66=\$616$

Therefore,

Simple interest earned by ben when $t=2$ years is $\$66$

Using Compound interest for Anica when $t=2$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=r=6\%=0.06$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}A=p{\left(1+\frac{r}{n}\right)}^{nt}\\ \Rightarrow A=550{\left(1+\frac{0.06}{1}\right)}^{2\left(1\right)}\\ \Rightarrow A=550{\left(1+0.06\right)}^2\\ \Rightarrow A=550{\left(1.06\right)}^2\\ \Rightarrow A=550\left(1.1236\right)\\ \Rightarrow A=\$617.98\end{array}$

Therefore,

To nearest cent, Total amount using compound interest $=A=\$617.98$

Interest earned $=$ Total Amount $-$ Principal amount

  $\Rightarrow$ Interest earned by Anica $=617.98-550=\$67.98$

We got

Compound interest earned by Anica is $\$67.98$

Using simple interest for Ben when $t=4$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=R=6\%$

We know

Annual interest rate $=r=\frac{R}{100}$

  $\begin{array}{l}\Rightarrow r=\frac{6}{100}\\ \Rightarrow r=0.06\end{array}$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}I=prt\\ \Rightarrow I=\left(550\right)\left(0.06\right)\left(4\right)\\ \Rightarrow I=132\end{array}$

Therefore,

Final amount $=$ Principal amount $+$ Simple interest.

  $\Rightarrow$ Final amount $=$$550+132=\$682$

Therefore,

Simple interest earned by ben when $t=4$ years is $\$132$

Using Compound interest for Anica when $t=4$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=r=6\%=0.06$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}A=p{\left(1+\frac{r}{n}\right)}^{nt}\\ \Rightarrow A=550{\left(1+\frac{0.06}{1}\right)}^{4\left(1\right)}\\ \Rightarrow A=550{\left(1+0.06\right)}^4\\ \Rightarrow A=550{\left(1.06\right)}^4\\ \Rightarrow A=550\left(1.26247696\right)\\ \Rightarrow A=\$694.362328\end{array}$

Therefore,

To nearest cent, Total amount using compound interest $=A=\$694.37$

Interest earned $=$ Total Amount $-$ Principal amount

  $\Rightarrow$ Interest earned by Anica $=694.37-550=\$144.37$

We got

Compound interest earned by Anica is $\$144.37$

Using simple interest for Ben when $t=6$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=R=6\%$

We know

Annual interest rate $=r=\frac{R}{100}$

  $\begin{array}{l}\Rightarrow r=\frac{6}{100}\\ \Rightarrow r=0.06\end{array}$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}I=prt\\ \Rightarrow I=\left(550\right)\left(0.06\right)\left(6\right)\\ \Rightarrow I=198\end{array}$

Therefore,

Final amount $=$ Principal amount $+$ Simple interest.

  $\Rightarrow$ Final amount $=$$550+198=\$748$

Therefore,

Simple interest earned by ben when $t=6$ years is $\$198$

Using Compound interest for Anica when $t=6$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=r=6\%=0.06$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}A=p{\left(1+\frac{r}{n}\right)}^{nt}\\ \Rightarrow A=550{\left(1+\frac{0.06}{1}\right)}^{6\left(1\right)}\\ \Rightarrow A=550{\left(1+0.06\right)}^6\\ \Rightarrow A=550{\left(1.06\right)}^6\\ \Rightarrow A=550\left(1.41851911\right)\\ \Rightarrow A=\$780.185511\end{array}$

Therefore,

To nearest cent, Total amount using compound interest $=A=\$780.19$

Interest earned $=$ Total Amount $-$ Principal amount

  $\Rightarrow$ Interest earned by Anica $=780.19-550=\$230.19$

We got

Compound interest earned by Anica is $\$230.19$

Using simple interest for Ben when $t=8$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=R=6\%$

We know

Annual interest rate $=r=\frac{R}{100}$

  $\begin{array}{l}\Rightarrow r=\frac{6}{100}\\ \Rightarrow r=0.06\end{array}$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}I=prt\\ \Rightarrow I=\left(550\right)\left(0.06\right)\left(8\right)\\ \Rightarrow I=264\end{array}$

Therefore,

Final amount $=$ Principal amount $+$ Simple interest.

  $\Rightarrow$ Final amount $=$$550+264=\$814$

Therefore,

Simple interest earned by ben when $t=8$ years is $\$264$

Using Compound interest for Anica when $t=8$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=r=6\%=0.06$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}A=p{\left(1+\frac{r}{n}\right)}^{nt}\\ \Rightarrow A=550{\left(1+\frac{0.06}{1}\right)}^{8\left(1\right)}\\ \Rightarrow A=550{\left(1+0.06\right)}^8\\ \Rightarrow A=550{\left(1.06\right)}^8\\ \Rightarrow A=550\left(1.59384807\right)\\ \Rightarrow A=\$876.616439\end{array}$

Therefore,

To nearest cent, Total amount using compound interest $=A=\$876.62$

Interest earned $=$ Total Amount $-$ Principal amount

  $\Rightarrow$ Interest earned by Anica $=876.62-550=\$326.62$

We got

Compound interest earned by Anica is $\$326.62$

Using simple interest for Ben when $t=10$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=R=6\%$

We know

Annual interest rate $=r=\frac{R}{100}$

  $\begin{array}{l}\Rightarrow r=\frac{6}{100}\\ \Rightarrow r=0.06\end{array}$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}I=prt\\ \Rightarrow I=\left(550\right)\left(0.06\right)\left(10\right)\\ \Rightarrow I=330\end{array}$

Therefore,

Final amount $=$ Principal amount $+$ Simple interest.

  $\Rightarrow$ Final amount $=$$550+330=\$880$

Therefore,

Simple interest earned by ben when $t=10$ years is $\$330$

Using Compound interest for Anica when $t=10$ years

From given information

Principal amount $=p=\$550$ .

Interest percent $=r=6\%=0.06$

On substituting values in above mentioned concept

We get

  $\begin{array}{l}A=p{\left(1+\frac{r}{n}\right)}^{nt}\\ \Rightarrow A=550{\left(1+\frac{0.06}{1}\right)}^{10\left(1\right)}\\ \Rightarrow A=550{\left(1+0.06\right)}^{10}\\ \Rightarrow A=550{\left(1.06\right)}^{10}\\ \Rightarrow A=550\left(1.7908477\right)\\ \Rightarrow A=\$984.966235\end{array}$

Therefore,

To nearest cent, Total amount using compound interest $=A=\$984.97$

Interest earned $=$ Total Amount $-$ Principal amount

  $\Rightarrow$ Interest earned by Anica $=984.97-550=\$434.97$

We got

Compound interest earned by Anica is $\$434.97$

Therefore, Table of calculated data

Years	Ben	Anica
2	$66	$67.98
4	$\$132$	$\$144.37$
6	$\$198$	$\$230.19$
8	$\$264$	$\$326.62$
10	$\$330$	$\$434.97$

b.

To determine

To find: Graph the data on the coordinate plane.

Explanation of Solution

Given information:

Principal amount of Ben $=\$550$

Simple interest percent of Ben $=6\%$

Principal amount of Anica $=\$550$ .

Compound Interest percent of Anica $=6\%$

If compounded annually value of $n$ is $1$ .

Explanation:

We got

Years	Ben	Anica
2	$66	$67.98
4	$\$132$	$\$144.37$
6	$\$198$	$\$230.19$
8	$\$264$	$\$326.62$
10	$\$330$	$\$434.97$

On graphing above data, we get

  

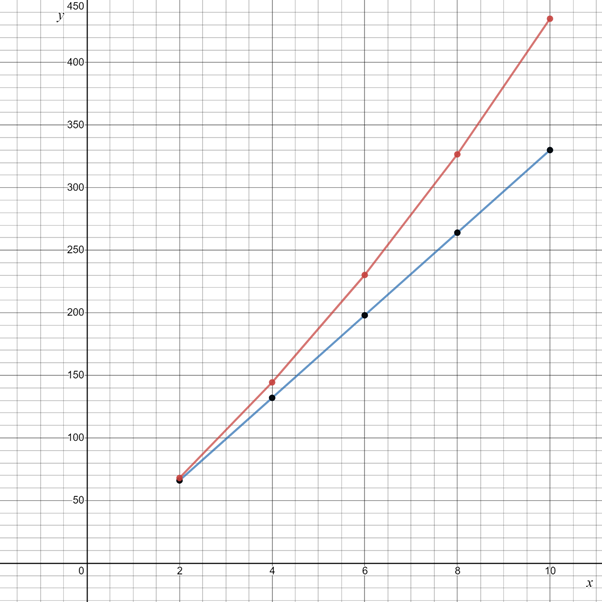
X-axis represents the time in years

Y-axis represents the total interest earned in dollars.

Blue line represents Ben’s interest balance.

Red line represents the Annica’s interest balance.

c.

To determine

To find: Compare the graph of two functions.

Answer to Problem 32IP

At every point Value of Compound interest that is Anica interest value is greater than value of Simple interest that is Ben interest value.

Explanation of Solution

Given information:

Principal amount of Ben $=\$550$

Simple interest percent of Ben $=6\%$

Principal amount of Anica $=\$550$ .

Compound Interest percent of Anica $=6\%$

If compounded annually value of $n$ is $1$ .

Explanation:

We got

Years	Ben	Anica
2	$66	$67.98
4	$\$132$	$\$144.37$
6	$\$198$	$\$230.19$
8	$\$264$	$\$326.62$
10	$\$330$	$\$434.97$

On graphing above data, we get

  

X-axis represents the time in years

Y-axis represents the total interest earned in dollars.

Blue line represents Ben’s interest balance.

Red line represents the Annica’s interest balance.

On comparing graph of both functions

We get

At every point Value of Compound interest that is Anica interest value is greater than value of Simple interest that is Ben interest value.

The graph of Ben’s interest is a straight line.

The graph of Anica’s interest is increasing at a faster rate and is not in a straight line.