
a.
To write the system of equations that represents the number of U.S. teams and non-U.S. teams.
a.
Answer to Problem 31PPS
Explanation of Solution
Given:
Number of professional mountain bike racing teams: 66
Number of non-U.S. teams is 30 more than the number of U.S. teams.
Calculation:
Let x represent the number of non-U.S. teams and y represent the number of U.S. teams.
The total number of professional mountain bike racing teams is 66.
So, it can be represented as:
Also, the number of non-U.S. teams is 30 more than the number of U.S. teams. Then,
Conclusion:
Therefore, the equations that represent the U.S. and Non-U.S. teams are
b.
To find the solution to the system of equations found in (a).
b.
Answer to Problem 31PPS
Explanation of Solution
Given:
From subpart (a),
The system of equations is:
Calculation:
Let the equations be labelled as follows:
Add the above equations.
Substitute
Say, Equation (2),
Conclusion:
Therefore, the solutions of the system of equations is
c.
To interpret the solution as the context of the question
c.
Answer to Problem 31PPS
Non-U.S. teams: 48
U.S. teams: 18
Explanation of Solution
Given:
From subpart (b),
Calculation:
Let x represent the number of non-U.S. teams and y represent the number of U.S. teams.
Then the number of non-U.S. teams is 48
The number of U.S. teams is 18.
Conclusion:
Therefore, the number of non-U.S. teams and U.S. teams are 48 and 18 respectively.
d.
Graph the system of equations and check the solution.
d.
Explanation of Solution
Given:
From subpart (a),
The system of equations is:
Graph:
Using a graphing utility the system of equations is graphed as follows:
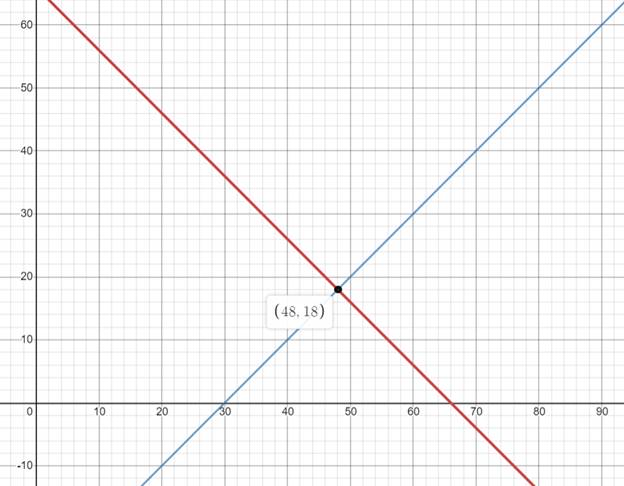
Interpretation:
From the above graph, the point of intersection of x and y co-ordinates is the same as the solutions found algebraically.
Conclusion:
Therefore, the solutions of the equations are verified graphically.
Chapter 6 Solutions
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
Additional Math Textbook Solutions
Introductory Statistics
Calculus: Early Transcendentals (2nd Edition)
College Algebra (7th Edition)
Thinking Mathematically (6th Edition)
Elementary Statistics (13th Edition)
Algebra and Trigonometry (6th Edition)
- Use the graph of y = f(x) to answer the following. 3- 2 -4 -2 -1 1 2 3 4 -1 2 m -3- + (d) Find all x for which f(x) = -2. If there is more than one value, separate them with commas or write your answer in interval notation, if necessary. Select "None", if applicable. Value(s) of x for which f(x)=-2: | (0,0) (0,0) (0,0) (0,0) 0,0... -00 None (h) Determine the range of f. The range is (0,0) Garrow_forwardWhat is g(f(4))arrow_forward10) Multiply (8m + 3)² A) 8m²+11m+6 B) m² + 48m+9 C) 64m²+48m+9 D) 16m²+11m+6arrow_forward
- Let R be field and X= R³/s Vector space over R M=(a,b,c)labic, e Rra+b= 3- <3 Show that Ms and why with proof. 1) is convexset and affine set of botost ii) is blanced set and symmetirs set of x iii) is hy per space and hyper plane ofx or hot iii) find f:MR st kerf = M 18/103 and finnd fiM→R/{0} st M= {xEX, f(t) = x, texiαER? jiii) show that Mis Maxsubspace or not and Mis a max. affine set or not.arrow_forwardFind The partial fraction decomposition for each The following 2× B) (x+3) a 3 6 X-3x+2x-6arrow_forward1) Find the partial feraction decomposition for each of 5- X 2 2x+x-1 The following: 3 B) 3 X + 3xarrow_forward
- Kate, Luke, Mary and Nancy are sharing a cake. The cake had previously been divided into four slices (s1, s2, s3 and s4). The following table shows the values of the slices in the eyes of each player. What is fair share to nancy? S1 S2 S3 S4 Kate $4.00 $6.00 $6.00 $4.00 Luke $5.30 $5.00 $5.25 $5.45 Mary $4.25 $4.50 $3.50 $3.75 Nancy $6.00 $4.00 $4.00 $6.00arrow_forwardKate, Luke, Mary and Nancy are sharing a cake. The cake had previously been divided into four slices (s1, s2, s3 and s4). The following table shows the values of the slices in the eyes of each player. S1 S2 S3 S4 Kate $4.00 $6.00 $6.00 $4.00 Luke $5.30 $5.00 $5.25 $5.45 Mary $4.25 $4.50 $3.50 $3.75 Nancy $6.00 $4.00 $4.00 $6.00 how much is the cak worth to maryarrow_forwardKate, Luke, Mary and Nancy are sharing a cake. The cake had previously been divided into four slices (s1, s2, s3 and s4). The following table shows the values of the slices in the eyes of each player. What is the threshold of fair share for Luke? S1 S2 S3 S4 Kate $4.00 $6.00 $6.00 $4.00 Luke $5.30 $5.00 $5.25 $5.45 Mary $4.25 $4.50 $3.50 $3.75 Nancy $6.00 $4.00 $4.00 $6.00arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





