Chapter 6.1, Problem 6.35P

The truss shown consists of six members and is supported by a short link at A. two short links at B, and a ball and socket at D. Determine the force in each of the members for the given loading.

To determine

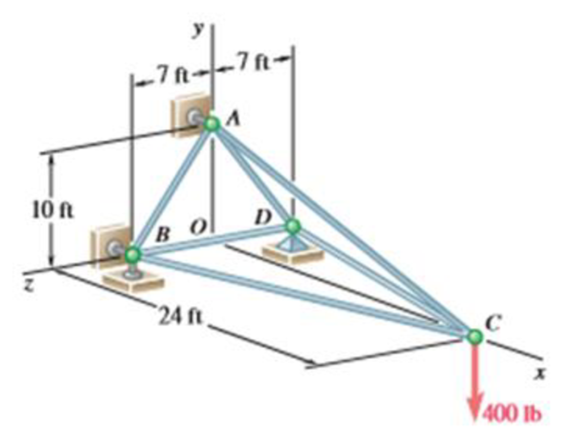
The force in each of the members of the truss for the given loading.

Answer to Problem 6.35P

The force in member AC is $1040\text{ lb}$ and the member AC is in tension, the force in members $BC\text{ and }CD$ is $500\text{ lb}$ and these members are in compression, the force in members $AB\text{ and }AD$ is $244\text{ lb}$ and these members are in compression, the force in member $BD$ is $280\text{ lb}$ and it is in tension.

Explanation of Solution

The free-body diagram of the entire truss is shown in figure 1.

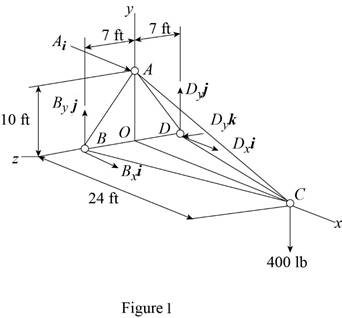
Refer to figure 1 and use symmetry.

$\begin{array}{c}{D}_x=B_x\\ D_y=B_y\end{array}$ (I)

Here, $D_x$ is the $x$ component of the reaction at the point D, $D_y$ is the $y$ component of the reaction at the point D, $B_x$ is the $x$ component of the reaction at the point B and $B_y$ is the $y$ component of the reaction at the point B.

Write the equilibrium equations taking the moments about $z$ axis.

$\Sigma M_z=0$ (II)

Here, $\Sigma M_z$ is the sum of the moments about $z$ axis.

Write the equation for $\Sigma M_z$ .

$\Sigma M_z=-A\left(10\text{ ft}\right)-\left(400\text{ lb}\right)\left(24\text{ ft}\right)$

Here, $A$ is the reaction at the point A.

Put the above equation in equation (II).

$\begin{array}{c}-A\left(10\text{ ft}\right)-\left(400\text{ lb}\right)\left(24\text{ ft}\right)=0\\ A=-960\text{ lb}\end{array}$

The $x$ component of the net force must be equal to zero.

$\Sigma {\overrightarrow{F}}_x=0$ (III)

Here, $\Sigma {\overrightarrow{F}}_x$ is the $x$ component of the net force.

Write the expression for $\Sigma {\overrightarrow{F}}_x$ .

$\Sigma {\overrightarrow{F}}_x=B_x+D_x+A$

Put the above equation in equation (III).

$B_x+D_x+A=0$

Put equation (I) in the above equation.

$\begin{array}{c}{B}_x+B_x+A=0\\ 2B_x+A=0\\ B_x=\frac{-A}{2}\end{array}$

Substitute $-960\text{ lb}$ for $A$ in the above equation to find $B_x$ .

$\begin{array}{c}{B}_x=\frac{-\left(-960\text{ lb}\right)}{2}\\ =480\text{ lb}\end{array}$

The $y$ component of the net force must be equal to zero.

$\Sigma {\overrightarrow{F}}_y=0$ (IV)

Here, $\Sigma {\overrightarrow{F}}_y$ is the $y$ component of the net force.

Write the expression for $\Sigma {\overrightarrow{F}}_y$ .

$\Sigma F_y=B_y+D_y-400\text{ lb}$

Put the above equation in equation (IV).

$B_y+D_y-400\text{ lb=0}$

Put equation (I) in the above equation.

$\begin{array}{c}{B}_y+B_y-400\text{ lb}=0\\ 2B_y-400\text{ lb}=0\\ B_y=200\text{ lb}\end{array}$

Write the expression for the reaction at the point B.

$\overrightarrow{B}=B_x\widehat{i}+B_y\widehat{j}$

Here $\overrightarrow{B}$ is the reaction at the point B.

Substitute $480\text{ lb}$ for $B_x$ and $200\text{ lb}$ for $B_y$ in the above equation to find $\overrightarrow{B}$ .

$\overrightarrow{B}=\left(480\text{ lb}\right)\widehat{i}+\left(200\text{ lb}\right)\widehat{j}$

Consider the free-body joint C. The free-body diagram of joint C is shown in figure 2.

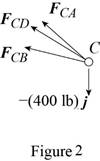
Refer to figure (2) and write the expression for the forces.

${\overrightarrow{F}}_{CA}=F_{AC}\frac{\overrightarrow{CA}}{CA}$ (V)

Here, ${\overrightarrow{F}}_{CA}$ is the force exerted by member CA and $CA$ is the magnitude of the vector $\overrightarrow{CA}$ .

Write the expression for $\overrightarrow{CA}$ .

$\overrightarrow{CA}=-24\widehat{i}+10\widehat{j}$

Find the magnitude of $\overrightarrow{CA}$ .

$\begin{array}{c}CA=\sqrt{{\left(-24\right)}^2+{10}^2}\\ =26\end{array}$

Substitute $-24\widehat{i}+10\widehat{j}$ for $\overrightarrow{CA}$ and $26$ for $CA$ in equation (V) to find the expression for ${\overrightarrow{F}}_{CA}$ .

${\overrightarrow{F}}_{CA}=F_{AC}\frac{\left(-24\widehat{i}+10\widehat{j}\right)}{26}$ (VI)

Write the expression for ${\overrightarrow{F}}_{CB}$ .

${\overrightarrow{F}}_{CB}=F_{BC}\frac{\overrightarrow{CB}}{CB}$

Here, ${\overrightarrow{F}}_{CB}$ is the force exerted by member CB and $CB$ is the magnitude of the vector $\overrightarrow{CB}$ .

Substitute $-24\widehat{i}+7\widehat{k}$ for $\overrightarrow{CB}$ and $25$ for $CB$ in the above equation to find the expression for ${\overrightarrow{F}}_{CB}$ .

${\overrightarrow{F}}_{CB}=F_{BC}\frac{\left(-24\widehat{i}+7\widehat{k}\right)}{25}$ (VII)

Write the expression for ${\overrightarrow{F}}_{CD}$ .

${\overrightarrow{F}}_{CD}=F_{CD}\frac{\overrightarrow{CD}}{CD}$

Here, ${\overrightarrow{F}}_{CD}$ is the force exerted by member CD and $CD$ is the magnitude of the vector $\overrightarrow{CD}$ .

Substitute $-24\widehat{i}-7\widehat{k}$ for $\overrightarrow{CD}$ and $25$ for $CD$ in the above equation to find the expression for ${\overrightarrow{F}}_{CD}$ .

${\overrightarrow{F}}_{CD}=F_{CD}\frac{\left(-24\widehat{i}-7\widehat{k}\right)}{25}$ (VIII)

The net force must be equal to zero.

$\Sigma \overrightarrow{F}=0$ (IX)

Here, $\Sigma \overrightarrow{F}$ is the net force.

Write the expression for $\Sigma \overrightarrow{F}$ .

$\Sigma \overrightarrow{F}={\overrightarrow{F}}_{CA}+{\overrightarrow{F}}_{CB}+{\overrightarrow{F}}_{CD}-\left(400\text{ lb}\right)\widehat{j}$

Put the above equation in equation (IX).

${\overrightarrow{F}}_{CA}+{\overrightarrow{F}}_{CB}+{\overrightarrow{F}}_{CD}-\left(400\text{ lb}\right)\widehat{j}=0$

Put equations (VI), (VII) and (VIII) in the above equation.

$F_{AC}\frac{\left(-24\widehat{i}+10\widehat{j}\right)}{26}+F_{BC}\frac{\left(-24\widehat{i}+7\widehat{k}\right)}{25}+F_{CD}\frac{\left(-24\widehat{i}-7\widehat{k}\right)}{25}-\left(400\text{ lb}\right)\widehat{j}=0$ (X)

Equate the coefficient of $\widehat{i}$ in equation (X) to zero.

$-\frac{24}{26}{F}_{AC}-\frac{24}{25}\left(F_{BC}+F_{CD}\right)=0$ (XI)

Equate the coefficient of $\widehat{j}$ in equation (X) to zero.

$\begin{array}{c}\frac{10}{26}{F}_{AC}-400\text{ lb}=0\\ F_{AC}=1040\text{ lb, tension}\end{array}$

Equate the coefficient of $\widehat{k}$ in equation (X) to zero.

$\begin{array}{c}\frac{7}{25}\left(F_{BC}-F_{CD}\right)=0\\ F_{CD}=F_{BC}\end{array}$ (XII)

Put the above equation in equation (XI).

$\begin{array}{c}-\frac{24}{26}{F}_{AC}-\frac{24}{25}\left(F_{BC}+F_{BC}\right)=0\\ -\frac{24}{26}{F}_{AC}-\frac{24}{25}\left(2F_{BC}\right)=0\end{array}$

Substitute $1040\text{ lb}$ for $F_{AC}$ in the above equation.

$\begin{array}{c}-\frac{24}{26}\left(1040\text{ lb}\right)-\frac{24}{25}\left(2F_{BC}\right)=0\\ F_{BC}=-500\text{ lb}\\ F_{BC}=500\text{ lb, compression}\end{array}$

Consider the free-body joint B. The free-body diagram of joint B is shown in figure 3.

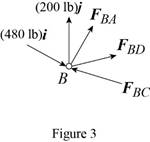
Refer to figure (3) and write the expression for the forces.

${\overrightarrow{F}}_{BC}=F_{BC}\frac{\overrightarrow{CB}}{CB}$ (XIII)

Here, ${\overrightarrow{F}}_{BC}$ is the force exerted by member BC

Substitute $500\text{ lb}$ for $F_{BC}$ , $-24\widehat{i}+7\widehat{k}$ for $\overrightarrow{CB}$ and $25$ for $CB$ in equation (XIII) to find the expression for ${\overrightarrow{F}}_{BC}$ .

$\begin{array}{c}{\overrightarrow{F}}_{BC}=\left(500\text{ lb}\right)\frac{\left(-24\widehat{i}+7\widehat{k}\right)}{25}\\ =-\left(480\text{ lb}\right)\widehat{i}+\left(140\text{ lb}\right)\widehat{k}\end{array}$ (XIV)

Write the expression for ${\overrightarrow{F}}_{BA}$ .

${\overrightarrow{F}}_{BA}=F_{AB}\frac{\overrightarrow{BA}}{BA}$

Here, ${\overrightarrow{F}}_{BA}$ is the force exerted by member BA and $BA$ is the magnitude of the vector $\overrightarrow{BA}$ .

Substitute $10\widehat{j}-7\widehat{k}$ for $\overrightarrow{BA}$ and $12.21$ for $BA$ in the above equation to find the expression for ${\overrightarrow{F}}_{BA}$ .

${\overrightarrow{F}}_{BA}=F_{AB}\frac{\left(10\widehat{j}-7\widehat{k}\right)}{12.21}$ (XV)

Write the expression for ${\overrightarrow{F}}_{BD}$ .

${\overrightarrow{F}}_{BD}=-F_{BD}\widehat{k}$ (XVI)

Here, ${\overrightarrow{F}}_{BD}$ is the force exerted by member BD

Write the expression for $\Sigma \overrightarrow{F}$ .

$\Sigma \overrightarrow{F}={\overrightarrow{F}}_{BA}+{\overrightarrow{F}}_{BD}+{\overrightarrow{F}}_{BC}+\overrightarrow{B}$

Put the above equation in equation (IX).

${\overrightarrow{F}}_{BA}+{\overrightarrow{F}}_{BD}+{\overrightarrow{F}}_{BC}+\overrightarrow{B}=0$

Put equations (XIV), (XV) and (XVI) in the above equation.

$-\left(480\text{ lb}\right)\widehat{i}+\left(140\text{ lb}\right)\widehat{k}+F_{AB}\frac{\left(10\widehat{j}-7\widehat{k}\right)}{12.21}-F_{BD}\widehat{k}+\overrightarrow{B}=0$

Substitute $\left(480\text{ lb}\right)\widehat{i}+\left(200\text{ lb}\right)\widehat{j}$ for $\overrightarrow{B}$ in the above equation.

$-\left(480\text{ lb}\right)\widehat{i}+\left(140\text{ lb}\right)\widehat{k}+F_{AB}\frac{\left(10\widehat{j}-7\widehat{k}\right)}{12.21}-F_{BD}\widehat{k}+\left(480\text{ lb}\right)\widehat{i}+\left(200\text{ lb}\right)\widehat{j}=0$ (XVII)

Equate the coefficient of $\widehat{j}$ in equation (XVII) to zero.

$\begin{array}{c}\frac{10}{12.21}{F}_{AB}+200\text{ lb}=0\\ F_{AB}=-244.2\text{ lb}\\ =244\text{ lb, compression}\end{array}$

Equate the coefficient of $\widehat{k}$ in equation (XVII) to zero.

$\begin{array}{c}-\frac{7}{12.21}{F}_{AB}-F_{BD}+140\text{ lb}=0\\ F_{BD}=-\frac{7}{12.21}{F}_{AB}+140\text{ lb}\end{array}$

Substitute $-244.2\text{ lb}$ for $F_{AB}$ in the above equation.

$\begin{array}{c}{F}_{BD}=-\frac{7}{12.21}\left(-244.2\text{ lb}\right)+140\text{ lb}\\ =280\text{ lb, tension}\end{array}$

From symmetry,

$F_{AD}=F_{AB}$

Here, $F_{AD}$ is the force exerted by AD.

Substitute $244\text{ lb, compression}$ for $F_{AB}$ in the above equation to find $F_{AD}$ .

$F_{AD}=244\text{ lb, compression}$

Conclusion:

Thus, the force in member AC is $1040\text{ lb}$ and the member AC is in tension, the force in members $BC\text{ and }CD$ is $500\text{ lb}$ and these members are in compression, the force in members $AB\text{ and }AD$ is $244\text{ lb}$ and these members are in compression, the force in member $BD$ is $280\text{ lb}$ and it is in tension.