
Calculating
a. If she starts making these deposits on her 36th birthday and continues to make deposits until she is 65 (the last deposit will be on her 65th birthday), what amount must she deposit annually to be able to make the desired withdrawals at retirement?
b. Suppose your friend has just inherited a large sum of money. Rather than making equal annual payments, she has decided to make one lump sum payment on her 35th birthday to cover her retirement needs. What amount does she have to deposit?
c. Suppose your friend’s employer will contribute $3,500 to the account every year as part of the company’s profit-sharing plan. In addition, your friend expects a $175,000 distribution from a family trust fund on her 55th birthday, which she will also put into the retirement account. What amount must she deposit annually now to be able to make the desired withdrawals at retirement?
a)
To calculate: The required savings for each year
Introduction:
The series of payments that are made in equal intervals is an annuity payment. The amount of annuity payments is mainly calculated based on the particular situation.
Answer to Problem 68QP
The required savings for each year is $11,776.01
Explanation of Solution
Given information:
Person X’s friend is celebrating her 35th birthday today as she wishes to start saving for her retirement at the age of 65. She wants to withdraw a sum of $105,000 on each of her birthdays for 20 years that is followed by her retirement in which, the first withdrawal will fall on her 66th birthday. She also intends to put her money in the local credit union that offers a 7% interest for a year. She also wishes to make equivalent annual payments on each of her birthdays into the account that is established at the Credit Union for retirement fund.
It is assumed that she starts making the deposit on her 36th birthday and continues to make it until her 65th birthday.
Timeline of the amount that is necessary for retirement is as follows:
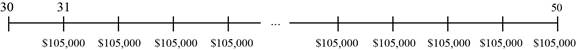
Note: In the above given information, every question is asked for a different cash flow but it is for the funding of the same retirement plan. Each of the saving possibility has the similar future value that refers to the present value of the spending on the retirement when Person X’s friend is ready for the retirement.
Formula to calculate the present value annuity is as follows:
Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period. Thus, by the present value of annuity, the amount that is essential for Person X’s friend is when she is ready for the retirement and it can be calculated as follows:
Compute the present value annuity:
Hence, the amount that is required for Person X’s friend at the time of retirement is $1,112,371.50
Note: The present value of annuity is same for all the necessary requirements.
The timeline that denotes when Person X’s friend makes equivalent annual deposits into the account and with the future value of annuity equivalent to the sum essential at the time of retirement is as follows:

Formula to calculate the future value annuity is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments. The future value of annuity represents the necessary savings for each year.
Compute the future value annuity:
Hence, the required savings for each year is $11,776.01.
b)
To calculate: The present value of the lump sum savings
Introduction:
The series of payments that are made in equal intervals is an annuity payment. The amount of annuity payments is mainly calculated based on the particular situation.
Answer to Problem 68QP
The present value of the lump sum savings is $146,129.04
Explanation of Solution
Given information:
Person X’s friend is celebrating her 35th birthday today as she wishes to start saving for her retirement at the age of 65. She wants to withdraw a sum of $105,000 on each of her birthdays for 20 years that is followed by her retirement in which, the first withdrawal will fall on her 66th birthday. She also intends to put her money in the local credit union that offers a 7% interest for a year. She also wishes to make equivalent annual payments on each of her birthdays into the account that is established at the Credit Union for retirement fund.
Person X’s friend has just inherited a large sum of money. She decides to make the lump sum payment on her 35th birthday to cover the needs of retirement rather than making equal annual payments.
Timeline for the lump sum saving amount is as follows:

Formula to compute the future value is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value:
Hence, the lump sum amount is $146,129.04
c)
To calculate: The annual contribution of Person X’s friend
Introduction:
The series of payments that are made in equal intervals is an annuity payment. The amount of annuity payments is mainly calculated based on the particular situation.
Answer to Problem 68QP
The annual contribution of Person X’s friend is $4,631.63
Explanation of Solution
Given information:
Person X’s friend is celebrating her 35th birthday today as she wishes to start saving for her retirement at the age of 65. She wants to withdraw a sum of $105,000 on each of her birthdays for 20 years that is followed by her retirement in which, the first withdrawal will fall on her 66th birthday. She also intends to put her money in the local credit union that offers a 7% interest for a year. She also wishes to make equivalent annual payments on each of her birthdays into the account that is established at the Credit Union for retirement fund.
The employer of Person X’s friend contributes a sum of $3,500 into her account each year as a part of sharing the profit. In addition, Person X’s friend also expects a sum of distribution from her family trust on her 55th birthday that amounts to $175,000.
Timeline of the lump sum saving in addition to the annual deposit is as follows:

Note: The value that is essential for retirement is known as the value of the lump sum saving at retirement can be subtracted to determine how much Person X’s friend is short of.
Formula to compute the future value of the trust fund deposit is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value of the trust fund deposit is as follows:
Hence, the future value of the trust fund deposit is $344,251.49.
The amount that Person X’s friend needs at retirement is calculated as follows:
Hence, the amount that Person X’s friend needs at the time of retirement is $768,120.01.
Note: The payment can be solved by using the equation of the future value of annuity.
Formula to calculate the future value annuity is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value annuity:
Hence, the total annual contribution is $8,131.63
Compute the contribution that is made by Person X’s friend is as follows:
Note: The contribution made by Person X’s friend is calculated by subtracting the employer’s contribution from the total annual contribution.
Hence, the contribution made by Person X’s friend is $4,631.63.
Want to see more full solutions like this?
Chapter 6 Solutions
Fundamentals of Corporate Finance
- General Financearrow_forwardAs CFO for Everything.Com, you are shopping for 6,000 square feet of usable office space for 25 of your employees in Center City, USA. A leasing broker shows you space in Apex Atrium, a 10-story multitenanted office building. This building contains 360,000 square feet of gross building area. A total of 54,000 square feet is interior space and is nonrentable. The nonrentable space consists of areas contained in the basement, elevator core, and other mechanical and structural components. An additional 36,000 square feet of common area is the lobby area usable by all tenants. The 6,000 square feet of usable area that you are looking for is on the seventh floor, which contains 33,600 square feet of rentable area, and is leased by other tenants who occupy a combined total of 24,000 square feet of usable space. The leasing broker indicated that base rents will be $30 per square foot of rentable area Required: a. Calculate total rentable area in the building as though it would be rented to…arrow_forwardDon't used Ai solutionarrow_forward
- General Finance Questionarrow_forwardConsider the following simplified financial statements for the Yoo Corporation (assuming no income taxes): Income Statement Balance Sheet Sales Costs $ 40,000 Assets 34,160 $26,000 Debt Equity $ 7,000 19,000 Net income $ 5,840 Total $26,000 Total $26,000 The company has predicted a sales increase of 20 percent. Assume Yoo pays out half of net income in the form of a cash dividend. Costs and assets vary with sales, but debt and equity do not. Prepare the pro forma statements. (Input all amounts as positive values. Do not round intermediate calculations and round your answers to the nearest whole dollar amount.) Pro forma income statement Sales Costs $ 48000 40992 Assets $ 31200 Pro forma balance sheet Debt 7000 Equity 19000 Net income $ 7008 Total $ 31200 Total 30304 What is the external financing needed? (Do not round intermediate calculations. Negative amount should be indicated by a minus sign.) External financing needed $ 896arrow_forwardAn insurance company has liabilities of £7 million due in 10 years' time and £9 million due in 17 years' time. The assets of the company consist of two zero-coupon bonds, one paying £X million in 7 years' time and the other paying £Y million in 20 years' time. The current interest rate is 6% per annum effective. Find the nominal value of X (i.e. the amount, IN MILLIONS, that bond X pays in 7 year's time) such that the first two conditions for Redington's theory of immunisation are satisfied. Express your answer to THREE DECIMAL PLACES.arrow_forward
- An individual is investing in a market where spot rates and forward rates apply. In this market, if at time t=0 he agrees to invest £5.3 for two years, he will receive £7.4 at time t=2 years. Alternatively, if at time t=0 he agrees to invest £5.3 at time t=1 for either one year or two years, he will receive £7.5 or £7.3 at times t=2 and t=3, respectively. Calculate the price per £5,000 nominal that the individual should pay for a fixed-interest bond bearing annual interest of 6.6% and is redeemable after 3 years at 110%. State your answer at 2 decimal places.arrow_forwardThe one-year forward rates of interest, f+, are given by: . fo = 5.06%, f₁ = 6.38%, and f2 = 5.73%. Calculate, to 4 decimal places (in percentages), the three-year par yield.arrow_forward1. Give one new distribution channels for Virtual Assistance (freelance business) that is not commonly used. - show a chart/diagram to illustrate the flow of the distribution channels. - explain the rationale behind it. (e.g., increased market reach, improved customer experience, cost-efficiency). - connect the given distribution channel to the marketing mix: (How does it align with the overall marketing strategy? Consider product, price, promotion, and place.). - define the target audience: (Age, gender, location, interests, etc.). - lastly, identify potential participants: (Wholesalers, retailers, online platforms, etc.)arrow_forward
 EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT

