
To calculate: The monthly savings of Person BB.
Introduction:
The series of payments that are made at equal intervals is an
Answer to Problem 57QP
The monthly savings of Person BB is $3,362.78.
Explanation of Solution
Given information:
Person BB wishes to save money to fulfill his three objectives. They are as follows:
- The first objective of Person BB is to retire at thirty years from now with a retirement amount of $20,000 for a month for every 25 years, the first payment will be expected at thirty years and a month from present
- The second objective of Person BB is to buy a cabin in the Place R within ten years at an projected cost of $375,000
- The third objective of Person B is to leave an inheritance of $2,000,000 to Person F after he passes on and at the last of the 25 years of withdrawal
Person BB can afford to save $25,000 for a month for the next ten years if he can earn the effective annual cost of 7% after his retirement and 10% before his retirement.
Time line of the cash flow:
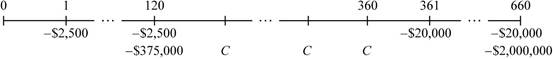
Note: The cash flows from the given information takes place monthly basis, the given interest rate is an effective annual rate. As the cash flows take place on a monthly basis, it is essential to compute the effective monthly rate by finding the annual percentage rate through monthly compounding, and then dividing it by 12. The preretirement annual percentage rate is calculated as follows:
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Compute the annual percentage rate with the effective annual rate:
Hence, the annual percentage rate is 0.0957 or 9.57%.
The annual percentage rate for the post-retirement is calculated as follows:
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Compute the annual percentage rate with the effective annual rate:
Hence, the annual percentage rate is 0.067 or 6.78%.
First, it is essential to compute the retirement needs of Person BB. The amount that is essential for the retirement is the present value of the monthly spending plus the inheritance’s present value. The present value of the two cash flows is as follows:
Formula to calculate the present value
Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period.
Compute the present value annuity for without fee:
Formula to calculate the present value:
Compute the present value:
Hence, the present value is $368,498.36.
Person BB will be saving $2,500 per month for the upcoming ten years until he buys the cabin. The value of his savings after ten years is calculated as follows:
Formula to calculate the
Note: C denotes the annual cash flow or the annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value annuity of Person BB:
Hence, the future value of the annuity is $499,659.64.
The amount that remains in the hands of Person BB after the purchase of the cabin is as follows:
Note: The amount that remains in the hands of Person BB is calculated by subtracting the cost of the cabin from the calculated future value of the annuity.
Hence, the amount that Person BB has in his hands is $124,659.64.
Person BB still has twenty years until the retirement and at the time when he is ready to retire, the amount he would receive is as follows:
Formula to compute the future value:
Note: C denotes the annual cash flow or the annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value:
Hence, the future value is $838,647.73.
Thus, when Person BB is ready for the retirement based on his present savings, he will be short of the below amount:
Thus, the above calculated amount is the future value of the monthly savings that Person BB has to make between ten to thirty years.
Hence, the future value of an annuity of Person BB is $2,415,347.07.
Compute the monthly savings of Person BB using the Formula of the future value of an annuity:
Hence, the monthly savings of Person BB is $3,362.78.
Want to see more full solutions like this?
Chapter 6 Solutions
Fundamentals of Corporate Finance
 EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT PFIN (with PFIN Online, 1 term (6 months) Printed...FinanceISBN:9781337117005Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning
PFIN (with PFIN Online, 1 term (6 months) Printed...FinanceISBN:9781337117005Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning Pfin (with Mindtap, 1 Term Printed Access Card) (...FinanceISBN:9780357033609Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning
Pfin (with Mindtap, 1 Term Printed Access Card) (...FinanceISBN:9780357033609Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning


