
Concept explainers
To calculate: The points that Person X will be willing to pay the interest rate
Introduction:
The total sum of interest that is due for a particular time is the interest rate. The interest rate can be due for a period as a proportion of the sum borrowed or deposited and as the proportion of the sum lent.
The annual rate that is earned from the investment or charged for a borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is calculated by multiplying the rate of interest for a period with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.
Answer to Problem 65QP
The maximum points that Person X would be willing to pay is 0.1601 or 1.601 points
Explanation of Solution
Given information:
Person X purchases a house and borrows $200,000 on a thirty year fixed rate mortgage. Person X has to pay on monthly basis to finance the purchase. The loan officer of Person X has offered him a mortgage with an annual percentage rate of 4%. The loan officer states Person X an alternative that he can buy down the rate of interest to 3.75% if he pays points up front on the loan. A point on the loan is 1% of the loan value.
Person X believes that he lives only for 8 years in the house before selling the house and purchase a new house. Thus, the Person X pays off the remaining balance of the real mortgage.
Note: The loan payment is for the first eight years and the remaining payment will be a balloon payment at the end. Thus there will be a 264-month payment.
Formula to calculate the monthly rate:
Compute the monthly rate with the original interest:
Hence, the monthly rate is 0.00333 or 0.333%
Formula to calculate the
Note: C represents the annual cash flow, r is the rate of exchange, and t denotes the period. The loan payments with the points are based on the original amount borrowed.
Compute the present value annuity:
Hence, the value for C is $954.83
Formula to calculate the balloon payment:
Note: C denotes the annual cash flow, r denotes the rate of exchange, and t denotes the period. The balloon payment is calculated using the formulae of the present value of annuity.
Compute the balloon payment using the formulae of the present value annuity:
Hence, the balloon payment is $167,460.95
Time line of the payments:
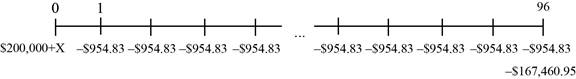
Compute the equation for amount borrowed:
Note: The actual amount that is received in front of the mortgage is the sum of borrowed amount and the points. Considering as X as the dollar amount of the points. The maximum number of points can be solved as it results in the cash flows that have a new rate of interest of 3.75%.
Formula to calculate the monthly rate:
Compute the monthly rate with the original interest:
Hence, the monthly rate is 0.00313 or 0.313%
Formula to calculate the present value annuity:
Note: To determine the maximum number of points that Person X is willing to pay, it is essential to set the annual percentage rate and the effective annual rate of loan with points and without points to be equal.
Compute the cash flows for maximum points using the formulae of present value annuity:
Hence, the maximum dollar amount is $3,202.16
Formula to calculate the maximum points:
Compute the maximum point:
Hence, the maximum points is 0.1601 or 1.601 points.
Want to see more full solutions like this?
Chapter 6 Solutions
Fundamentals of Corporate Finance
- What is the 50/30/20 budgeting rule in finance?arrow_forwardHow do student loans impact long-term financial health?arrow_forwardWith regard to foreign currency translation methods used by foreign MNCs, Multiple Choice a. foreign currency translation methods are generally only used by U.S. based MNCs since foreign firms have a built-in hedge by being foreign. b. are generally the same methods used by U.S.-based firms. c. are exactly the same methods used by U.S.-based firms since GAAP is GAAP. d. none of the options.arrow_forward
- Cray Research sold a supercomputer to the Max Planck Institute in Germany on credit and invoiced €11.60 million payable in six months. Currently, the six-month forward exchange rate is $1.18 per euro and the foreign exchange adviser for Cray Research predicts that the spot rate is likely to be $113 per euro in six months.Required: a. What is the expected gain/loss from a forward hedge?Note: A Negative value should be indicated with a minus sign. Do not round intermediate calculations. Round your final answer in whole dollars not in millions.arrow_forwardWhat is the time value of money and how is it calculated? need answer!arrow_forwardHelp me in this question! What is the time value of money and how is it calculated?arrow_forward
 PFIN (with PFIN Online, 1 term (6 months) Printed...FinanceISBN:9781337117005Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning
PFIN (with PFIN Online, 1 term (6 months) Printed...FinanceISBN:9781337117005Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning Pfin (with Mindtap, 1 Term Printed Access Card) (...FinanceISBN:9780357033609Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning
Pfin (with Mindtap, 1 Term Printed Access Card) (...FinanceISBN:9780357033609Author:Randall Billingsley, Lawrence J. Gitman, Michael D. JoehnkPublisher:Cengage Learning


