
Calculating
To calculate: The size of settlements, and if Person X is a plaintiff, what will be his choice on the interest rate.
Introduction:
The series of payments that are made at equal intervals is an annuity payment. The amount of annuity payments is calculated mainly based on the particular situation.
Answer to Problem 61QP
The size of the settlement or the award is $476,773.21.
Explanation of Solution
Given information:
Person X serves on a jury. A plaintiff sues the city for the injuries that continued after the accident of a sweeper in the Street F. In the trial, the doctors stated that it will be 5 years earlier the plaintiff is able to return back to work. The decision made by the jury was in favor of the plaintiff. Person X is the foreperson of the jury, the jury proposes that the plaintiff will be provided an award that is as follows:
- a) The present value of the 2 years back pay. The annual salary of the plaintiff for the last 2 years would have been $43,000 and $46,000.
- b) The present value of the 5 years’ salary in future is assumed to be $51,000 for a year.
- c) The sum that has to be paid for the pain and suffering is $150,000.
- d) The amount of the court costs is $20,000.
It has to be assumed that the payment of the salary is made at the end of the month in equal amounts. The rate of interest is 8% at an effective annual rate.
Time line of the cash flow:
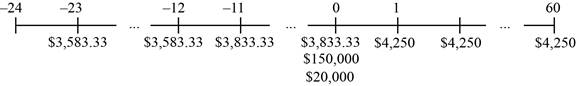
Note: The cash flows here would have happened in the past and will also occur in the future. It is essential to find the present cash flows. Before computing the present value of the cash flow, it is essential to adjust the rate of interest and thus, the effective monthly interest rate can be found. Finding the annual percentage rate with compounding monthly and dividing it by twelve will provide the effective monthly rate. The annual percentage rate with the monthly compounding is calculated as follows:
Compute the annual percentage rate with the effective annual rate:
Hence, the annual percentage rate is 0.0772 or 7.72%.
To determine the today’s value of the back pay from 2 years ago, it is essential to find the future value of annuity and then the lump sums future value.
Formula to calculate the future value of an annuity:
Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period.
Compute the future value annuity:
Hence, the future value of annuity is $44,554.76.
Formula to compute the future value:
Note: C denotes the annual cash flow or annuity payment, r represents the rate of interest, and t denotes the number of payments.
Compute the future value:
Hence, the future value is $48,119.14088.
Note: The future value of the annuity is determined by the effective monthly rate and the future value of the lump sum is determined by the effective annual rate. The other alternate way to determine the future value of the lump sum with the effective annual rate as long it is utilized for the 12 periods. The solution would be the same in either way.
Now the today’s value of the last year’s back pay is calculated as follows:
Compute the future value annuity:
Hence, the future value of the annuity is $47,663.23.
Next, it is essential to determine today’s value of the 5 year’s future salary.
Formula to calculate the present value annuity:
Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period.
Compute the present value annuity for without fee:
Hence, the present value of the annuity is $210,990.8393.
The today’s value of the jury award is calculated by adding the sum of salaries, the court costs, and the compensation for the pain and sufferings. The award amount is calculated as follows:
Hence, the award amount or the size of the settlement is $476,773
To determine: As a plaintiff the choice of Person X on the interest rate.
Introduction:
The series of payments that are made at equal intervals is an annuity payment. The amount of annuity payments is calculated mainly based on the particular situation.
Explanation of Solution
As a plaintiff, Person X will choose the lesser interest rate. In this problem, both the future value and the present value is calculated. The lesser interest rate decreases the future value of the annuity and increases the present value of the annuity.
Thus, by the lesser interest rate, the value of the back pay is lowered. But, the present value of the future salary is increased. Since the salary in the future is longer and larger, it is the more significant cash flow to the plaintiff.
Want to see more full solutions like this?
Chapter 6 Solutions
Fundamentals of Corporate Finance
- I need help with this situation and financial accounting questionarrow_forwardRemaining Time: 50 minutes, 26 seconds. * Question Completion Status: A Moving to the next question prevents changes to this answer. Question 9 Question 9 of 20 5 points Save Answer A currency speculator wants to speculate on the future movements of the €. The speculator expects the € to appreciate in the near future and decides to concentrate on the nearby contract. The broker requires a 2% Initial Margin (IM) and the Maintenance Margin (MM) is 75% of IM. Following € Futures quotes are currently available from the Chicago Mercantile Exchange (CME). Euro (CME)- €125,000; $/€ Open High Low Settle Change Open Interest June 1.2216 1.2276 1.2175 1.2259 -0.0018 Sept 1.2229 1.2288 1.2189 1.2269 0.0018 255,420 19,335 In addition to the information provided above, consider the following CME quotes that are available at the end of day one's trading: Euro (CME) - €125,000; $/€ Open High Low June 1.2216 Sept 1.2229 1.2276 1.2288 Settle Change Open Interest 1.2175 1.2176 -0.0083 255,420 1.2189…arrow_forwardI need help with this problem and financial accounting questionarrow_forward
