Chapter 6, Problem 6.40P

Interpretation Introduction

(a)

Interpretation:

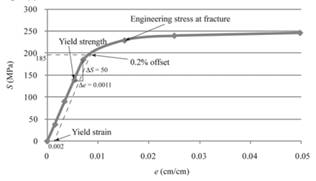
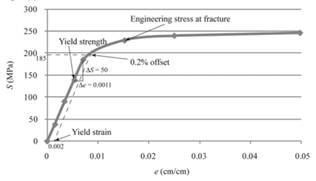
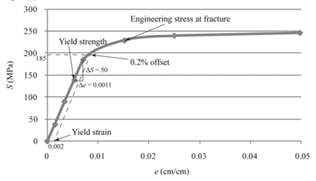
The engineering stress-strain curve should be plotted and the 0.2 % offset yield strength should be calculated for the given data of magnesium.

Concept Introduction:

The maximum amount of elastic deformation which is bearable by any material is defined as yield strength.

Answer to Problem 6.40P

The yield strength for 0.2% offset is 185MPa for a given sample of magnesium.

Explanation of Solution

The tabular data providing details about the load and length difference for a given sample is as follows:

Calculate the engineering stress for the sample of with the help of below formula:

Load (lb.)	$\Delta l$ (mm)
0	0.00000
5000	0.0296
10,000	0.0592
15,00	0.0888
20,000	0.15
25,000	0.51
26,500	0.90
27,000	1.50 (fracture)
26,500	2.10
25,000	2.79 (maximum load)

$\begin{array}{l}S=\frac{F}{A}\\ S=\frac{F}{\frac{\pi }{4}\times d^2}\mathrm{.....}(1)\\ S=\frac{F}{\frac{\pi }{4}\times {\left(12mm\right)}^2}\\ S=\frac{F}{113.1\text{}{\text{mm}}^2}\mathrm{....}(2)\end{array}$

In the equation (2), put value of F =5,000 N,

$\begin{array}{l}S=\frac{5,000\text{ N}}{113.1\text{}{\text{mm}}^2}.\times \frac{\text{}1{\text{mm}}^2}{{10}^{-6}{m}^2}\times \frac{1\text{MPa}}{{10}^{6}N/m^2}\\ S=44.20\text{}\text{MPa}\end{array}$

The below mentioned tabular data represent the value of engineering stress at different load applied at the given specimen of magnesium:

F(N)	S (MPa)
0	0
5000	44.20
10,000	88.40
15,00	132.60
20,000	176.80
25,000	221.04
26,500	234.30
27,000	238.72
26,500	234.30
25,000	221.04

Calculate the engineering strain for the sample of with the help of below formula:

$\begin{array}{l}e=\frac{\Delta l}{l_0}\\ e=\frac{\Delta l}{l_0}(l_0=30mm\text{}\text{ and }\Delta \text{l=0}\text{.0296}\text{}\text{mm)}\\ e=\frac{0.0296}{33}\\ e=9.8666\times {10}^{-4}\end{array}$

The below mentioned tabular data represent the value of engineering stress at different load applied at the given specimen of magnesium:

$\Delta l$ (cm)	e (cm/cm)
0.00000	0
0.0296	$9.8666\times {10}^{-4}$
0.0592	$1.973\times {10}^{-3}$
0.0888	$2.96\times {10}^{-3}$
0.15	$5\times {10}^{-3}$
0.51	0.017
0.90	0.030
1.50	0.050
2.10	0.070
2.79	0.093

With the use of given both spread sheets, one can tabulate the engineering stress and strain curve as follows:

  

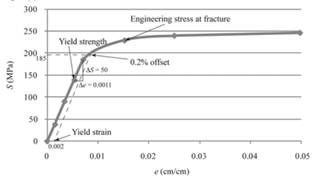
The above graph can provide the value of yield strength for 0.2% offset as 185 MPa.

Therefore, one can conclude that magnesium sample contains the yield strength for 0.2% offset as 185MPa.

Interpretation Introduction

(b)

Interpretation:

With the help of plotted engineering stress-strain curve, the tensile strength should be calculated.

Concept Introduction:

The tensile strength can be defined as the measurement of maximum deformation which can be bearable by any material without undergoing necking condition.

Answer to Problem 6.40P

The tensile strength is 239 MPa for a given sample of magnesium.

Explanation of Solution

With the use of a given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:

F(N)	S (MPa)	$\Delta l$ (cm)	e (cm/cm)
0	0	0.00000	0
5000	44.20	0.0296	$9.8666\times {10}^{-4}$
10,000	88.40	0.0592	$1.973\times {10}^{-3}$
15,00	132.60	0.0888	$2.96\times {10}^{-3}$
20,000	176.80	0.15	$5\times {10}^{-3}$
25,000	221.04	0.51	0.017
26,500	234.30	0.90	0.030
27,000	238.72	1.50	0.050
26,500	234.30	2.10	0.070
25,000	221.04	2.79	0.093

  

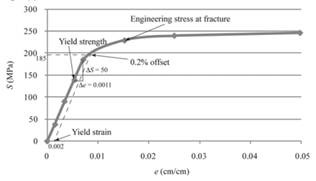
The tensile strength can be determined by use of below mentioned formula:

$\begin{array}{l}\text{ Tensile strength =}\frac{F_{\max imum\text{}\text{load}}}{A_0}\\ \text{ Tensile strength =}\frac{F_{\max imum\text{}\text{load}}}{\frac{\pi }{4}{d}^2}\\ \text{ Tensile strength =}\frac{27,000}{\frac{\pi }{4}{\left(12\right)}^2}\\ \text{ Tensile strength =}\frac{27,000}{113.1}\\ \text{ Tensile strength =238}\text{.72}\text{}\text{MPa}\\ \text{Tensile strength =239}\text{}\text{MPa}\end{array}$

Therefore, one can conclude that the given sample of magnesium has the tensile strength of 239 MPa.

Interpretation Introduction

(c)

Interpretation:

With the help of plotted engineering stress-strain curve, the value of modulus of elasticity should be calculated.

Concept Introduction:

Modulus of elasticity is also known as coefficient of elasticity or elastic modulus and can be defined as the ratio of the stress in the given object body to the corresponding strain.

Answer to Problem 6.40P

The value of modulus of elasticity is 45,455 MPa for a given magnesium.

Explanation of Solution

With the use of a given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:

F(N)	S (MPa)	$\Delta l$ (cm)	e (cm/cm)
0	0	0.00000	0
5000	44.20	0.0296	$9.8666\times {10}^{-4}$
10,000	88.40	0.0592	$1.973\times {10}^{-3}$
15,00	132.60	0.0888	$2.96\times {10}^{-3}$
20,000	176.80	0.15	$5\times {10}^{-3}$
25,000	221.04	0.51	0.017
26,500	234.30	0.90	0.030
27,000	238.72	1.50	0.050
26,500	234.30	2.10	0.070
25,000	221.04	2.79	0.093

  

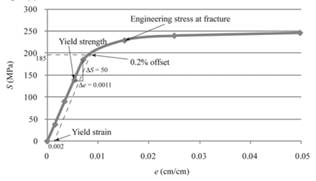
The modulus of elasticity can be determined by use of below mentioned formula:

$E=\frac{\Delta S}{\Delta e}\mathrm{......}(3)$

In above equation, $\Delta S$ is the stress related ordinate of slope and $\Delta e$ is strain related ordinate of slope. Putting the values of $\Delta S$ and $\Delta e$ as 50 MPa and 0.0011 respectively in above equation (3).

$\begin{array}{l}E=\frac{\Delta S}{\Delta e}\\ E=\frac{50}{0.0011}\\ E=45,455\text{}\text{MPa}\end{array}$

Therefore, the value of modulus of elasticity for given magnesium is 45,455 MPa.

Interpretation Introduction

(d)

Interpretation:

With the help of plotted engineering stress-strain curve, the value of % elongation should be calculated.

Concept Introduction:

Elongation is defined as term used to determine the change in gauge length of any material when it is on static tension test.

Answer to Problem 6.40P

The value of % elongation is 8.7% for a given magnesium.

Explanation of Solution

With the use of a given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:

F(N)	S (MPa)	$\Delta l$ (cm)	e (cm/cm)
0	0	0.00000	0
5000	44.20	0.0296	$9.8666\times {10}^{-4}$
10,000	88.40	0.0592	$1.973\times {10}^{-3}$
15,00	132.60	0.0888	$2.96\times {10}^{-3}$
20,000	176.80	0.15	$5\times {10}^{-3}$
25,000	221.04	0.51	0.017
26,500	234.30	0.90	0.030
27,000	238.72	1.50	0.050
26,500	234.30	2.10	0.070
25,000	221.04	2.79	0.093

  

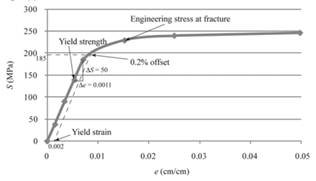
The following formula is used for determining the value of % elongation.

$\begin{array}{l}\%\text{ Elongation =}\frac{l-l_0}{l_0}\times 100\%\\ \%\text{ Elongation =}\frac{32.61-30}{30}\times 100\%\\ \%\text{ Elongation =8}\text{.7\%}\end{array}$

Therefore, the value of % elongation is 8.7% for given magnesium sample.

Interpretation Introduction

(e)

Interpretation:

With the help of plotted engineering stress-strain curve, the value of % reduction in area should be calculated.

Concept Introduction:

Reduction if area of any material is directly related to the reduction in cross-section area of the tensile test piece after fracture.

Answer to Problem 6.40P

The value of % reduction in area is 4.3% for given magnesium.

Explanation of Solution

With the use of given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:

F(N)	S (MPa)	$\Delta l$ (cm)	e (cm/cm)
0	0	0.00000	0
5000	44.20	0.0296	$9.8666\times {10}^{-4}$
10,000	88.40	0.0592	$1.973\times {10}^{-3}$
15,00	132.60	0.0888	$2.96\times {10}^{-3}$
20,000	176.80	0.15	$5\times {10}^{-3}$
25,000	221.04	0.51	0.017
26,500	234.30	0.90	0.030
27,000	238.72	1.50	0.050
26,500	234.30	2.10	0.070
25,000	221.04	2.79	0.093

  

One can use the following formula for determining the value of % reduction in area.

$\begin{array}{l}{A}_{redcution}=\frac{\frac{\pi }{4}{\left(d\right)}^2-\frac{\pi }{4}{\left(d_0\right)}^2}{\frac{\pi }{4}{\left(d\right)}^2}\times 100\\ A_{redcution}=\frac{\frac{\pi }{4}{\left(12\right)}^2-\frac{\pi }{4}{\left(11.74\right)}^2}{\frac{\pi }{4}{\left(12\right)}^2}\times 100\\ A_{redcution}=\frac{113.1-108.24}{113.1}\times 100\\ A_{redcution}=4.29\%\\ A_{redcution}=4.3\%\end{array}$

Therefore, the given magnesium sample carries 4.3% the value of % reduction in area.

Interpretation Introduction

(f)

Interpretation:

With the help of plotted engineering stress-strain curve, the true stress should be determined at necking.

Concept Introduction:

True stress can be defined as the applied force or load that is divided by the cross-sectional area of specimen or object. It can be also defined as the required amount of force that tends to deformation of specimen.

Answer to Problem 6.40P

The trues stress is 251 MPa for given magnesium at necking.

Explanation of Solution

With the use of given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as follows:

F(N)	S (MPa)	$\Delta l$ (cm)	e (cm/cm)
0	0	0.00000	0
5000	44.20	0.0296	$9.8666\times {10}^{-4}$
10,000	88.40	0.0592	$1.973\times {10}^{-3}$
15,00	132.60	0.0888	$2.96\times {10}^{-3}$
20,000	176.80	0.15	$5\times {10}^{-3}$
25,000	221.04	0.51	0.017
26,500	234.30	0.90	0.030
27,000	238.72	1.50	0.050
26,500	234.30	2.10	0.070
25,000	221.04	2.79	0.093

  

The true stress at necking can be calculated with the use of below mentioned formula:

$\begin{array}{l}\sigma =S\left(1+e\right)\\ \sigma =\frac{F_{\mathrm{maxi}mum\text{ load}}}{A_0}\left(\frac{1+\Delta l_{\max imum\text{ load}}}{l_0}\right)\mathrm{.....}(4)\\ \sigma =\frac{F_{\mathrm{maxi}mum\text{ load}}}{\frac{\pi }{4}{d}_{s\tan dard}{}^2}\left(\frac{1+\Delta l_{\max imum\text{ load}}}{l_0}\right)\end{array}$

In the above equation, putting the values to determine true stress as below.

$\begin{array}{l}\sigma =\frac{F_{\mathrm{maxi}mum\text{ load}}}{A_0}\left(\frac{1+\Delta l_{\max imum\text{ load}}}{l_0}\right)\\ \sigma =\frac{27,000}{\left(\frac{\pi }{4}{\left(12\right)}^2\right)}\left(1+\frac{1.50}{30}\right)\\ \sigma =\frac{27,000}{113.1}\left(1.05\right)\\ \sigma =250.66\text{ MPa}\\ \sigma =251\text{ MPa}\end{array}$

Therefore, the given sample of magnesium has 251 MPa as a trues stress value at necking.

Interpretation Introduction

(g)

Interpretation:

With the help of plotted engineering stress-strain curve, the value of modulus of resilience should be determined.

Concept Introduction:

The amount of energy required to get absorbed by the material to return back to its original state is defined as resilience.

Modulus of resilience can be defined as the energy required by the material to return from its stress condition from zero to the yield stress limit.

Answer to Problem 6.40P

The value of modulus of resilience is 0.132 MPa of given magnesium.

Explanation of Solution

With the use of given spread sheet and applied loads, one can tabulate the engineering stress and strain curve as below:

F(N)	S (MPa)	$\Delta l$ (cm)	e (cm/cm)
0	0	0.00000	0
5000	44.20	0.0296	$9.8666\times {10}^{-4}$
10,000	88.40	0.0592	$1.973\times {10}^{-3}$
15,00	132.60	0.0888	$2.96\times {10}^{-3}$
20,000	176.80	0.15	$5\times {10}^{-3}$
25,000	221.04	0.51	0.017
26,500	234.30	0.90	0.030
27,000	238.72	1.50	0.050
26,500	234.30	2.10	0.070
25,000	221.04	2.79	0.093

  

The value of yield strength and strain is 132 MPa and 0.002 respectively.

$\begin{array}{l}\text{Resilience =}\frac{1}{2}\left(\text{yield strength}\right)\left(\text{strain at yield}\right)\\ \text{Resilience =}\frac{1}{2}\left(132\right)\left(0.002\right)\\ \text{Resilience =0}\text{.132}\text{}\text{MPa}\end{array}$

Therefore, the sample of magnesium has 0.132 MPa as the value of modulus of resilience.