Chapter 6, Problem 6.66P

Interpretation Introduction

(a)

Interpretation:

The transition temperature of each ductile cast iron considering energy absorbed in the ductile and brittle region by plotting results of Charpy impact test.

Concept Introduction:

Here, the graph for ductile cast iron with the different silicon content needs to be plotted. The graph represents temperature distribution vs. impact energy of each ductile cast iron. The transition temperature is obtained by absorbed energy in the brittle and ductile region.

Answer to Problem 6.66P

The transition temperature of each ductile cast iron are:

1. Ductile cast iron with 2.55%Si = 26.56 ⁰C
2. Ductile cast iron with 2.85% Si = 35.93 ⁰C
3. Ductile cast iron with 3.25% Si = 45 ⁰C
4. Ductile cast iron with 3.63% Si = 65 ⁰C

  

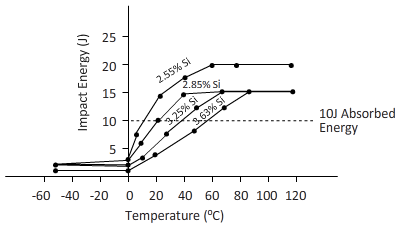
Explanation of Solution

Given Information:

Test Temperature (0C)	2.55%Si	2.85%Si	3.25%Si	3.63%Si
-50	2.5	2.5	2	2
-5	3	2.5	2	2
0	6	5	3	2.5
25	13	10	7	4
50	17	14	12	8
75	19	16	16	13
100	19	16	16	16
125	19	16	16	16

Calculations:

Transition temperature can be calculated by finding mean absorbed energy in the brittle and ductile region.

Thus,

1. For 2.55%Si Ductile cast iron:

Mean absorbed energy,

$\begin{array}{l}{E}_{2.55\%Si}=2.5+\frac{[19+2.5]}{2}\\ =13.25Joule\end{array}$

Transition temperature for 2.55%Si Ductile cast iron by interpolation,

$\begin{array}{l}{T}_{2.55\%Si}=25+\frac{[50-25]}{[17-13]}(13.25-13)\\ =26.5625{}^{0}C\end{array}$

2. For 2.85%Si Ductile cast iron:

Mean absorbed energy,

$\begin{array}{l}{E}_{2.85\%Si}=2.5+\frac{[16+2.5]}{2}\\ =11.75Joule\end{array}$

Transition temperature for 2.85%Si Ductile cast iron by interpolation,

$\begin{array}{l}{T}_{2.85\%Si}=25+\frac{[50-25]}{[14-10]}(11.75-10)\\ =35.9375{}^{0}C\end{array}$

3. For 3.25%Si Ductile cast iron:

Mean absorbed energy,

$\begin{array}{l}{E}_{3.25\%Si}=2+\frac{[16+2]}{2}\\ =11Joule\end{array}$

Transition temperature for 3.25%Si Ductile cast iron by interpolation,

$\begin{array}{l}{T}_{3.25\%Si}=25+\frac{[50-25]}{[12-7]}(11-7)\\ ={45}^{0}C\end{array}$

4. For 3.63%Si Ductile cast iron:

Mean absorbed energy,

$\begin{array}{l}{E}_{3.63\%Si}=2+\frac{[16+2]}{2}\\ =11Joule\end{array}$

Transition temperature for 3.63%Si Ductile cast iron by interpolation,

$\begin{array}{l}{T}_{3.63\%Si}=50+\frac{[75-50]}{[13-8]}(11-8)\\ =65{}^{0}C\end{array}$

Interpretation Introduction

(b)

Interpretation:

The transition temperature which provides 10 J of absorbed energy during the Charpy impact test needs to be determined.

Concept Introduction:

The transition temperature at 10 J absorbed energy can be calculated by considering the graph of temperature distribution vs. impact energy of each ductile cast iron.

Answer to Problem 6.66P

The transition temperature of each ductile cast iron for 10J of absorbed energy are:

1. Ductile cast iron with 2.55%Si = 14.28 ⁰C
2. Ductile cast iron with 2.85% Si = 25 ⁰C
3. Ductile cast iron with 3.25% Si = 40 ⁰C
4. Ductile cast iron with 3.63% Si = 60 ⁰C

Explanation of Solution

The transition temperature of each steel at 10J impact energy can be obtained from interpolation easily

  

1. For 2.55%Si Ductile cast iron:

$\begin{array}{l}{T}_{2.55\%Si}=0+\frac{[25-0]}{[13-6]}(10-6)\\ ={14.285}^{0}C\end{array}$

2. For 2.85%Si Ductile cast iron:

$\begin{array}{l}{T}_{2.85\%Si}=25{}^{0}C\\ \end{array}$

3. For 3.25%Si Ductile cast iron:

$\begin{array}{l}{T}_{3.25\%Si}=25+\frac{[50-25]}{[12-7]}(10-7)\\ ={40}^{0}C\end{array}$

4. For 3.63%Si Ductile cast iron:

$\begin{array}{l}{T}_{3.63\%Si}=50+\frac{[75-50]}{[13-8]}(10-8)\\ ={60}^{0}C\end{array}$

Interpretation Introduction

(c)

Interpretation:

The effect of silicon on the toughness of the ductile cast iron needs to be explained by plotting results of temperature versus silicon content. The maximum content of silicon used in ductile cast iron needs to be determined, when the part is used at 25⁰C.

Concept Introduction:

Here, the graph for silicon content vs. temperature needs to be plotted. The graph represents temperature distribution with silicon content in ductile cast iron.

Answer to Problem 6.66P

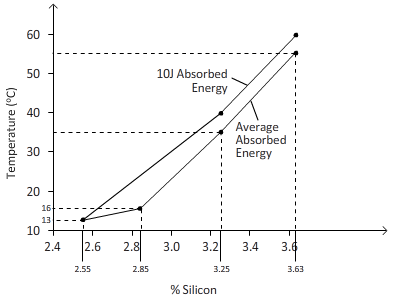
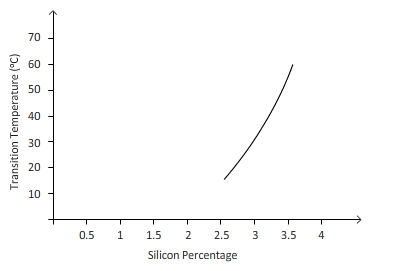
Considering the graph for silicon content vs. temperature, as silicon content increases, toughness decreases.

When ductile cast iron is used at 25 ⁰C, there should be at least 2.9% silicon allowable in cast iron.

Explanation of Solution

Following are the results of transition temperatures for different types of silicon content in ductile cast iron.

Silicon content (%)	Transition Temperature (0C)
2.55	15
2.85	25
3.25	40
3.63	60

Following graph shows the distribution of temperatures with different silicon content in ductile cast iron.

  

Effect of silicon on the toughness of ductile cast iron:

• According to the graph, the toughness of material decreases with an increase in the percentage of silicon.
• Also, transition temperature increases with an increase in silicon content in ductile cast iron.
• Hence from the graph, when ductile cast iron is used at 25 ⁰C, maximum 2.9% silicon is permissible in cast iron.